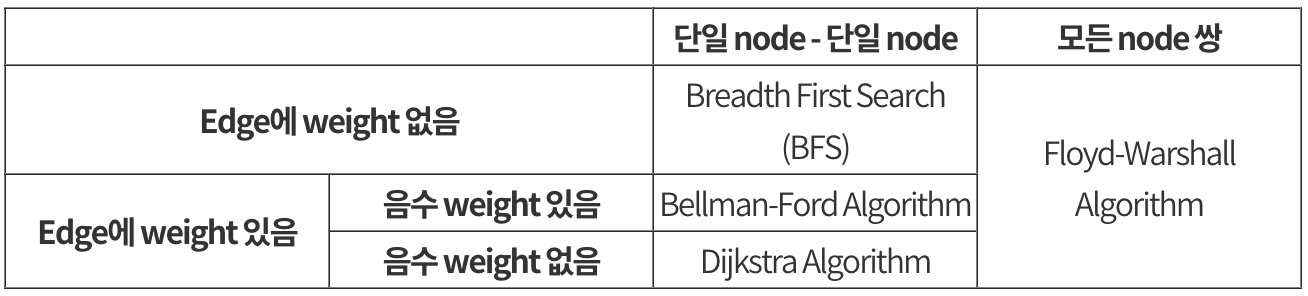
그래프에서 최단거리 구하는 방법
🎞️ Breadth First Search
BFS/너비 우선 탐색
- 시작 노드로부터 인접한 노드 먼저 방문
- 모든 노드들의 최단 거리 계산
- 용도: 두 노드 사이의 최단 경로/임의의 경로가 필요한 경우
- 트리에서 사용 가능
과정
- 시작 노드 방문
- 방문한 노드는 체크 (큐에 방문한 노드 삽입)
- 큐에서 꺼낸 노드와 인접한 노드는 모두 차례로 방문
- 인접한 노드가 (더이상) 없으면 큐의 앞에서 노드를 꺼냄
- 큐에 방문된 노드를 삽입
- 큐가 소진될때까지 반복
코드
class Graph {
private int V; // 총 노드 개수
private LinkedList<Integer> adj[]; // 인접리스트
/** 생성자 **/
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i) {
adj[i] = new LinkedList();
}
}
/** 단방향 노드 연결 **/
void addEdge(int v, int w) {
adj[v].add(w);
}
/** s노드부터 시작하는 BFS. 탐색한 노드 출력 **/
void BFS(int s) {
// 노드 방문 여부 (초기값: false)
boolean visited[] = new boolean[V];
// 큐 생성
LinkedList<Integer> queue = new LinkedList<Integer>();
// 현재 노드 방문 체크. 큐에 삽입
visited[s] = true;
queue.add(s);
// 큐가 빌 때까지 시작 노드와 인접한 노드 방문
while (queue.size() != 0) {
s = queue.poll();
System.out.print(s + " ");
}
}
}
🎞️ 다익스트라 (Dijkstra) 알고리즘
다이나믹 프로그래밍을 활용한 최단경로 탐색 알고리즘
- 특정 노드에서 다른 모든 정점으로 가는 최단 경로를 알려줌
- 음의 가중치가 없는 그래프에서만 활용
과정
- 출발 노드 설정
- 출발 노드를 기준으로 각 노드의 최소 비용 저장 (첫 노드는 0으로 초기화)
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드 선택 (그리디 알고리즘)
- 방문한 노드는 방문한 노드 리스트에 추가 & 방문 안한 노드 리스트에서 삭제
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용 갱신 (다이나믹 프로그래밍)
- 3~4 반복
시간복잡도
우선순위 큐(힙)을 사용하지 않고 구현하면 O(V^2)
우선순위 큐를 사용하면
- 모든 간선이 한번씩 검사됨 > O(E)
- 각 간선마다 우선순위 큐에 자료 삽입 연산 O(E*log E)
- 주로 그래프는 V^2 > E이므로 O(log E) = O(log V)
- 결과: 시간 복잡도: O(E*log V)
public class Dijkstra {
static class Node {
int idx;
int cost
Node(int idx, int cost) {
this.idx = idx;
this.cost = cost;
}
}
static ArrayList<Node>[] graph;
static boolean[] visited;
static int[] distance;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(br.readLine());
graph = new ArrayList[v+1];
visited = new boolean[v+1];
distance = new int[v+1];
for (int i = 1; i <= v; i++) {
graph[i] = new ArrayList<>();
distance[i] = Integer.MAX_VALUE; // 최단거리를 찾기 위해 최대값으로 초기화
}
for (int i = 0; i < e; i++) {
// u -> v로 가는 가중치 w가 주어짐
st = new StringTokenizer(br.readLine());
int inputU = Integer.parseInt(st.nextToken());
int inputV = Integer.parseInt(st.nextToken());
int inputW = Integer.parseInt(st.nextToken());
graph[inputU].add(new Node(inputV, inputW));
}
dijkstra(k);
for (int i = 1; int <= v; i++) {
System.out.println(dist[i] == Integer.MAX_VALUE ? "INF" : dist[i]);
}
}
static void dijkstra(int start) {
// 우선순위 큐 사용, 가중치를 기준으로 오름차순
PriorityQueue<Node> q = new PriorityQueue<>((o1, o2) -> o1.cost - o2.cost);
// 시작노드에 대해서 초기화
q.add(new Node(start, 0));
distance[start] = 0;
while (!q.isEmpty()) {
// 현재 최단 거리가 가장 짧은 노드를 꺼내서 방문 처리
Node now = q.poll();
if (!viist[now.v]) {
visit[now.v] = true;
}
for (Node next : graph[now.v]) {
// 방문하지 않은 노드 중 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 노드
if (!visit[next.v] && distance[next.v] > now.cost + next.cost) {
distance[next.v] = now.cost + next.cost;
q.add(new Node(next.v, distance[next.v]));
}
}
}
}
}🎞️ 벨만-포드 (Bellman-Ford) 알고리즘
벨만-포드 알고리즘: 한 노드에서 다른 노드까지의 최단 거리 구하기
- 간선의 가중치가 음수일 때도 적용 가능
- (총 정점 - 1)번의 매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리 구하기
과정
- 출발 노드 설정
- 최단 거리 테이블 초기화
- 다음의 과정을 (총 정점-1)번 반복
- 모든 간선 E개를 하나씩 확인
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
- 음수 간선 순환이 발생하는지 체크하려면 3번 과정을 한 번 더 수행
- 이 때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것
시간복잡도: O(VE)
V번 반복에 대해서 해당 정점과 연결되어 있는 모든 간선(E)을 탐색해서 시간복잡도는 O(VE)
코드
import sys
input = sys.stdin.readline
INF = int(1e9)
# 노드의 개수, 간선의 개수를 입력
v, e = map(int, input().split())
# 모든 간선에 대한 정보 담는 리스트
edges = []
# 최단 거리 테이블 초기화 (무한)
distance = [INF] * (v + 1)
# 모든 간선의 정보 입력
for _ in range(e):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c임 (a -> b의 비용이 c)
edges.append((a, b, c))
def bellman_ford(start):
# 시작 노드 초기화
distance[start] = 0
# 전체 (v-1)번 반복
for i in range(v):
# 반복마다 모든 간선 확인
for j in range(e):
current_node = edges[j][0]
next_node = edges[j][1]
edge_cost = edges[j][2]
# 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧을 때
if distance[current_node] != INF and distance[next_node] > distance[current_node] + edge_cost:
distance[next_node] = distance[current_node] + edge_cost
# v번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
if i == v - 1:
retun True
return False🎞️ 플로이드-워셜 (Floyd-Warshall) 알고리즘
- 모든 최단 경로를 구하는 알고리즘
- 한번 실행으로 모든 노드 간 최단 경로 구할 수 있음
- 음의 간선에도 사용 가능
- 거쳐가는 노드를 중점으로 경로 계산
- (X에서 노드1로 가는 비용 + 노드1에서 Y로 가는 비용) vs. X에서 Y로 가는 최소 비용의 비교
시간복잡도
- 각 단계마다 O(N^2)의 연산으로 현재 노드를 거쳐가는 모든 경로 고려
- 총 시간복잡도: O(N^3)
과정
- 2차원 인접 행렬 구성
- 라운드마다 각 경로에서 새로운 중간 노드로 사용할 수 있는 노드를 선택
public void floydWarshall() {
int distance[n][n];
// 결과 그래프를 기존 그래프로 초기화
for (int i = 0; i < num; i++) {
for (int j = 0; j < num; j++) {
d[i][j] = a[i][j];
}
}
// k: 거쳐가는 노드
for (int k = 0; k < num; k++) {
// i: 출발 노드
for (int i = 0; i < num; i++) {
// j: 도착 노드
for (int j = 0; j < number; j++) {
if (d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
// 결과 출력
for (int i = 0; i < num; i++) {
for (int j = 0; j < num; j ++) {
System.out.print(d[i][j]));
}
System.out.println();
}
}🎞️ 정점의 개수가 N개, 간선의 개수가 N^3 개라면, 어떤 알고리즘이 효율적인가
다익스탈: O(Elog V) = O(N^3log N)
벨만 포드: O(VE) = O(N^4)
플로이드-워셜: O(N^3) = O(N^3)
플로이드-워셜 알고리즘이 가장 효율적임
🎞️ A* 알고리즘
A* 알고리즘:
- 다익스트라 알고리즘 확장
- 가중치 그래프에서 시작 노드에서 목표 노드까지의 최단 경로만 구하고자 함
- 그리디 알고리즘
개념
- F = 출발 지점에서 목적지까지 총 cost 합
- G = 현재 노드에서 출발 지점까지의 총 cost
- H = Heuristic: 현재 노드에서 목적지까지의 추정거리
- Heuristic 함수를 설계하는 방법에 따라 성능 결정됨
- (예) 맨해턴 거리 함수, 유클리디안 거리 함수 등
F = G + H- H = 0이면 F = G가 됨
- 이 경우, 다익스트라 알고리즘과 동일하게 동작
- H = 0이면 F = G가 됨
- 가장 작은 F를 찾기 위해 우선순위 큐 사용
A* 알고리즘 vs. 다익스트라
A* 알고리즘은 음의 가중치도 계산 가능
🎞️ 음수의 간선/사이클
음수 간선/사이클이 존재하면 다익스트라 알고리즘은 부적합
- 다익스트라 알고리즘에서는 시작 정점에서 목표 정점에 도달하기까지 인접 간선들을 탐색하면서 최소 비용을 찾을 때마다 거리 값을 갱신함
- 이 과정에서 음수 사이클을 만나면 사이클을 돌수록 비용이 줄어든다고 알고리즘이 판단함
- 사이클 안에서 계속해서 맴돌다가 결국 도달할 수 없는 정점 발생
벨만-포드
- 모든 정점을 V-1번 방문하면 각 정점별 최단경로가 확정되어야 함
- V번째 방문에도 최단경로가 갱신되면 음수 사이클 검출
플로이드-워셜 알고리즘은 자기 자신에게 가는 간선 거리를 검사해서 음수 사이클을 검출함
- 자기 자신을 경로로 갖는 loop edge가 존재하고 그게 음수 가중치를 갖지 않는 한 그 경로는 0이여야 함
- 음수 사이클이 존재하면 음수 사이클에서 순회한 뒤 다시 자기 자신을 방문하여 음수가 되어 최단 거리로 취급됨
참고:
