[세그먼트 트리] 개념 및 응용 (C++ 구현)

beegle·2025년 1월 12일
세그먼트 트리
3

자료구조&알고리즘

목록 보기
1/6
post-thumbnail

들어가기 앞서…

이 글은 세그먼트 트리를 한번 쯤은 써본 사람들을 기준으로 작성하였습니다.

그래도 기본 개념부터 핵심 코드 설명까지 꽤나 자세하게 작성하였습니다. 또 어떤 점에서 이득이 있는지, 응용을 어떻게 하는지, 어떤 문제에 적용할 수 있는지 등 전체적으로 정리하는 느낌으로 써봤습니다.
혼자 여러 블로그 보면서 독학한 내용을 정리한 것이라 좀 설명이 난잡할 수 있지만 최대한 깔끔하게 정리하려고 노력하며 작성했습니다.

기본 개념

세그먼트 트리는 구간 쿼리(합, 곱 같은 계산)를 효율적으로 다룰 수 있는 자료구조이다.

누적합을 이용하면 구간 계산은 O(1)에 가능하지만 갱신의 경우가 O(N)으로 느리다는 한계점이 있다.

누적합으로는 갱신이 조금만 많아져도 못 풀기 때문에 이런 문제를 해결하기 위해서 세그먼트 트리를 사용한다. “구간 합 구하기”와 같은 세그트리 기본 문제를 DP나 누적합을 이용해서 풀 수 없나 열심히 생각해보면 왜 세그트리를 써야하는지 조금 더 이해가 가능하다.

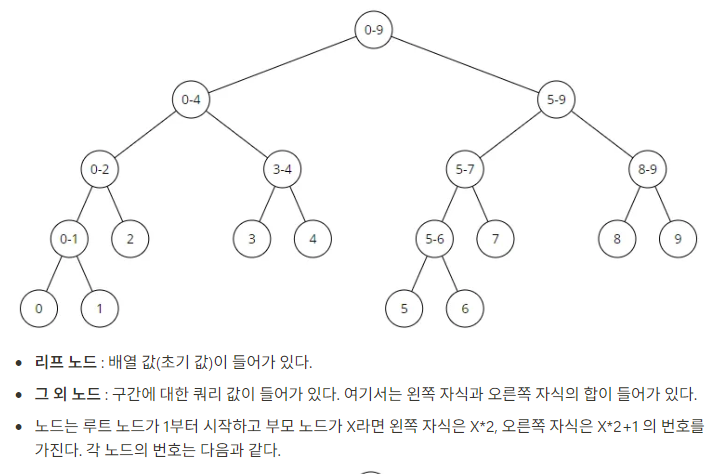
N = 10 인 경우의 세그먼트 트리는 다음과 같다.

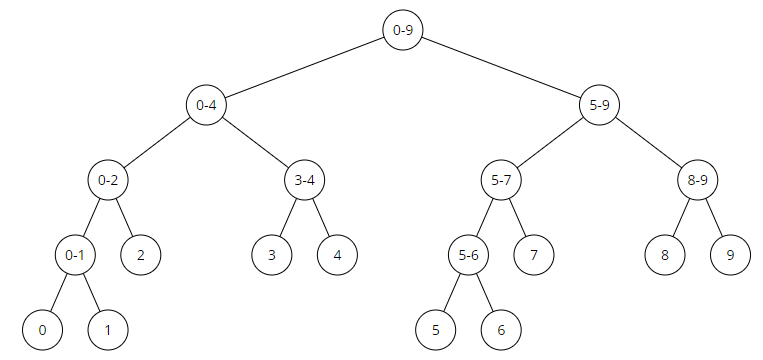
  • 리프 노드 : 배열 값(초기 값)이 들어가 있다.
  • 그 외 노드 : 구간에 대한 쿼리 값이 들어가 있다. 여기서는 왼쪽 자식과 오른쪽 자식의 합이 들어가 있다.
  • 노드는 루트 노드가 1부터 시작하고 부모 노드가 X라면 왼쪽 자식은 2X, 오른쪽 자식은 2X+1 의 번호를 가진다. 각 노드의 번호는 다음과 같다.

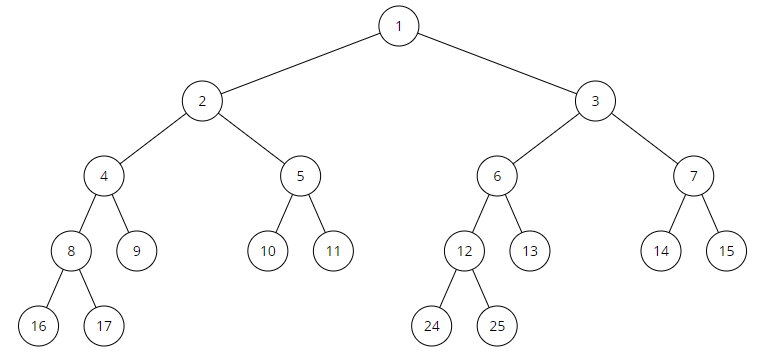
  • 리프 노드 의 개수가 N개이고, 리프 노드가 아닌 노드의 개수는 N-1개가 있어 총 노드의 개수는 2N -1개 있다. 하지만 트리를 만들 때, 크기를 2N-1으로 하지 않고 4*N으로 만드는데 그 이유는 완전 이진 트리로 만들기 때문이다.
  • 트리의 높이는 H=⌈log⁡N⌉
  • 높이가 H인 완전 이진 트리의 노드 개수는 배열 크기가 되고, 이 값은 2H+1−12^{H+1} - 1 이다.
  • 세그먼트 트리의 크기를 정확히 계산하고 싶으면 H = ceil(log(n))으로 두고 2H+1−12^{H+1} - 1 으로 계산해서 크기를 정해주면 되지만 귀찮기도 하고 실수할 확률이 높기 때문에 보통 4*N으로 두는 편이다.
  • 계산해보면 4*N은 절대 넘지 않는다는 것을 알 수 있다. ex) N=9일 때, 크기는 31이므로 3N보다는 크고 4N보다는 작은 것을 볼 수 있다.

특징

  • 구간 쿼리와 갱신을 둘 다 O(logN)O(logN)으로 줄일 수 있다.
  • 완전 이진 트리 구조이며 크기는 보통 넉넉잡아 4*N으로 만든다.
  • 기존 트리와 다르게 각 노드에 구간에 대한 정보가 담겨있다. ex) [1~4] 범위의 합
  • 리프 노드에는 배열 값(초기 값)이 들어가 있다.
  • 기본적으로 3개의 함수를 가진다.
    1. init 함수 : 초기값으로 세그먼트 트리를 만드는 함수
    2. update 함수 : 특정 위치 값을 특정 값으로 갱신하는 함수
    3. query 함수 : 구간 합, 곱 등등 특정 계산을 수행하고 값을 리턴해주는 함수
  • 위 함수를 기본으로 조금씩 변형해가며 응용한다. 특히 쿼리 함수가 문제마다 구하는 것에 따라 전부 다르다고 볼 수 있다.
  • 세그트리를 응용하는 알고리즘이 많기 때문에 거의 알고리즘이라고 생각해도 무방.

구현

  1. 세그먼트 트리 구축 (init 함수)

    ll init(int node, int s, int e){ // ll = long long
    if (s == e) return tree[node] = arr[s]; //리프 노드
    int m = (s + e) / 2;
    return tree[node] = init(node * 2, s, m) + init(node * 2 + 1, m + 1, e);
}
    • 구간은 [s(start), e(end)]
    • s==e 인 경우가 리프 노드인 경우이므로 배열의 값을 저장해 준다.
    • 현재 node의 왼쪽 자식은 node*2이고 오른쪽 자식은 node*2+1 입니다. 왼쪽 구간은 [s,m], 오른쪽 구간은 [m+1, e]이 된다.
    • tree[node]은 왼쪽 자식과 오른쪽 자식의 합이므로 재귀를 통해 구해준다.

  2. query 함수 (여기서는 구간의 합)

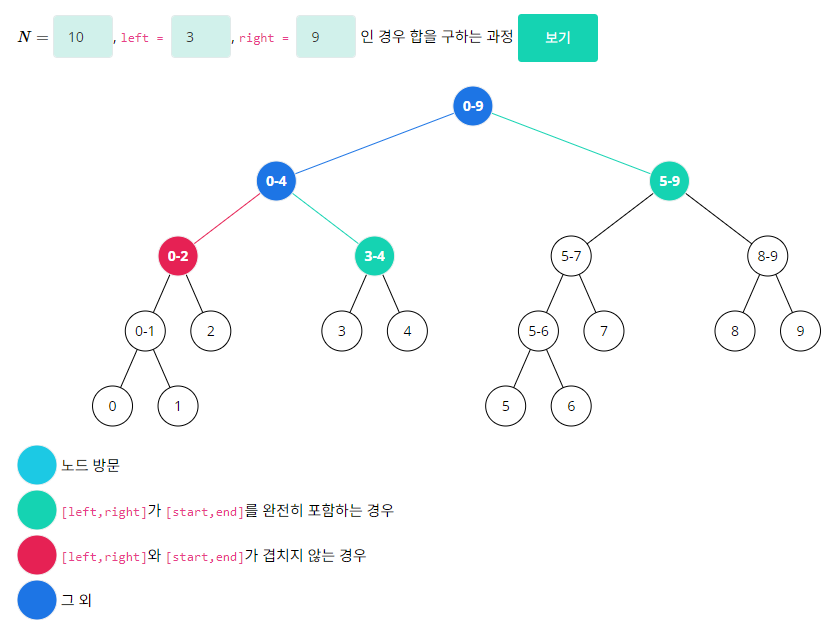
    ll sum(int node, int s, int e, int l, int r) {
    if (l > e || r < s) return 0; // 범위가 겹치지 않는 경우
    if (l <= s && e <= r) { // [l,r]가 [s,e]를 완전히 포함하는 경우
        return tree[node];
    }
    int m = (s + e) / 2;
    return sum(node * 2, s, m, l, r)
        + sum(node * 2 + 1, m + 1, e, l, r);
}

    [s,e] 은 처음에는 [1,n]으로 들어오며 계속 바뀌는 범위이다.

    [l,r] 은 우리가 원하는 범위로 바뀌지 않는 찾는 범위이다.

    이 둘의 범위에 따라 크게 3가지 경우의 수로 나눠진다.

    1. [left,right]와 [start,end]가 겹치지 않는 경우
      1. 구하는 범위를 [s,e]가 벗어났으니 더 이상 탐색할 필요가 없다.
    2. [left,right]가 [start,end]를 완전히 포함하는 경우
      1. 이미 구하는 범위 내에 [s,e]가 포함되었으니 더 이상 범위를 줄여가며 탐색할 필요가 없고 현재 tree[node]값을 리턴해준다.
    3. 그 외
      1. 왼쪽 범위와 오른쪽 범위로 쪼개가며 탐색을 이어간다.

    아래는 N=10일 때 예시이다.
    https://book.acmicpc.net/ds/segment-tree 이 사이트에서 직접 값을 바꿔가며 시도해볼 수 있다.

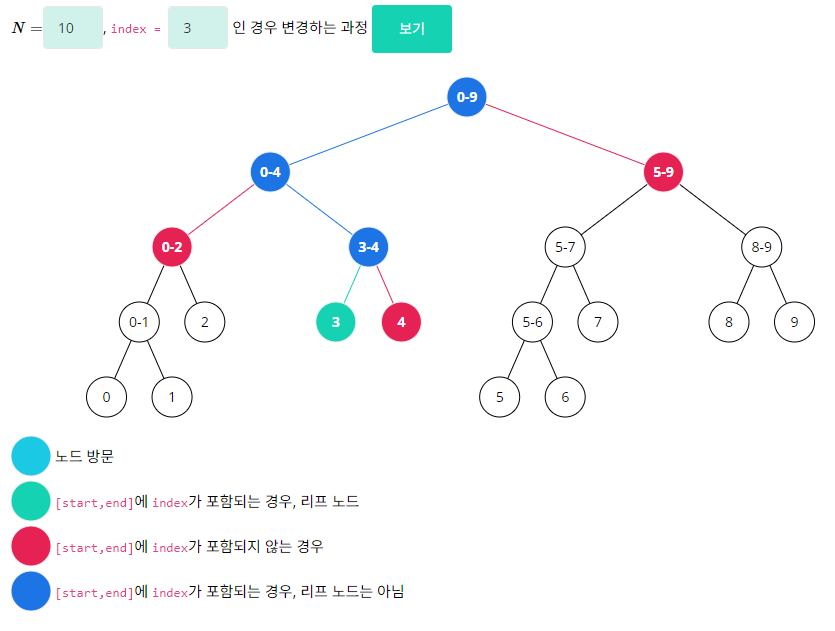
  3. update 함수 (값 변경)

    void update(int node, int s, int e, int idx, ll val) {
    if (idx < s || idx > e) return; // 범위 밖
    if (s == e) { // idx 찾음
        tree[node] = val;
        return;
    }
    int m = (s + e) / 2;
    update(node * 2, s, m, idx, val);
    update(node * 2 + 1, m + 1, e, idx, val);
    tree[node] = tree[node * 2] + tree[node * 2 + 1];
}

    여기서는 크게 범위에 따라 세 가지로 나뉜다.

    1. [start,end]에 index가 포함되지 않는 경우
      1. 찾는 idx가 범위를 벗어났으니 재귀 종료
    2. start == end 인 경우 = idx에 도착했을 때
      1. tree[node] 값을 변경해주고 리턴.
    3. 그 외
      1. 범위를 쪼개가며 탐색
      2. tree[node]를 왼쪽 자식과 오른쪽 자식의 합으로 갱신.

    이 방법은 리프 노드를 갱신하고 재귀를 타고 올라오면서 트리를 갱신하는 방식이고

    반대로 내려가면서 즉시 갱신하는 방식으로 해도 된다. 위에 링크를 올린 사이트에서는 내려가면서 갱신하는 방식으로 짰다.

문제 풀이

백준) 2042. 구간 합 구하기

세그먼트 트리의 가장 기본 문제로 구간 합을 구하는 문제다.

위에서 설명한 함수만 구현해주면 풀리는 간단한 문제다.

  • C++ 전체 코드
    #include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef vector<int> vi;
typedef vector<ll> vll;
typedef pair<int, int> pi;
typedef pair<ll, ll> pll;

const int N = 1000100;

vll tree, arr;

ll init(int node, int s, int e){
    if (s == e) return tree[node] = arr[s]; //리프 노드
    int m = (s + e) / 2;
    return tree[node] = init(node * 2, s, m) + init(node * 2 + 1, m + 1, e);
}

ll sum(int node, int s, int e, int l, int r) {
    if (l > e || r < s) return 0; // 범위 밖
    if (l <= s && e <= r) { // 범위 안
        return tree[node];
    }
    int m = (s + e) / 2;
    return sum(node * 2, s, m, l, r)
        + sum(node * 2 + 1, m + 1, e, l, r);
}

void update(int node, int s, int e, int idx, ll val) {
    if (idx < s || idx > e) return; // 범위 밖
    if (s == e) { // idx 찾음
        tree[node] = val;
        return;
    }
    int m = (s + e) / 2;
    update(node * 2, s, m, idx, val);
    update(node * 2 + 1, m + 1, e, idx, val);
    tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
int main() {
    ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);

    int n, m, k;
    cin >> n >> m >> k;

    tree = vll(4 * N);
    arr = vll(N);

    for (int i = 1; i <= n; i++) {
        cin >> arr[i];
        //update(1, 1, n, i, arr[i]);
    }
    init(1, 1, n);

    for (int i = 0; i < m + k; i++) {
        int op; cin >> op;
        if (op == 1) {// update
            ll a, b; cin >> a >> b;
            update(1, 1, n, a, b);
        }
        else if (op == 2) {// sum
            ll a, b; cin >> a >> b;
            cout << sum(1, 1, n, a, b) << '\n';
        }
    }

    return 0;
}

다음과 같이 함수 실행

  • update(1, 1, n, a, b)
  • sum(1, 1, n, a, b)

이 코드에서 범위를 [1~n]으로 했는데 [0~n-1]으로 해도 된다. [0~n], [1,N] 등 범위가 포함만 되어있으면 어찌 됐든 돌아가긴 한다. 한 마디로 크게는 상관 없지만, 아무래도 최적화를 위해 맞춰주는게 좋다고 생각한다.
이 문제에서 범위 입력값이 1~n으로 주어지기 때문에 그렇게 짠 거 뿐이다. 만약 범위를 [0~n-1]로 하게 되면 update(1,0,n-1,a-1,b-1) 이런식으로 범위를 조정해줘야 한다.

하지만 node는 꼭 1부터 시작해야 한다!!! 0*2는 계속해서 0이기 때문에 큰일난다.

init 함수는 초기에 세그먼트 트리를 구축하는 함수인데

이 문제와 같이 초기 배열값을 넣어주는 경우에는 굳이 init 함수를 짜지 않고 입력받을 때마다 update를 해주기도 한다. (주석 처리 해둔 부분)
init 함수를 쓰면 따로 입력값도 배열에 담아줘야 하고 함수도 짜야되고 귀찮다.

물론 처음에 모든값에 1을 넣어준다거나 배열 값을 계속 바꿔주고 넣어줘야 되는 경우가 있는데 그런 경우에는 init함수를 만들어주는 편이다.

그런데 사실 시간복잡도 차이를 보면 init 함수를 쓰는게 이득이다.
init함수는 O(N)이고, 매번 update로 하게되면 O(NlogN)이므로 init 함수를 만드는게 더 빠르다.

걸린 시간을 보면 위가 init 함수를 안 쓴것(380ms)이고 아래가 init 함수를 쓴 것(208ms)이다.

시간차이가 꽤 있는 편이라 좀 놀랬다..
물론 이 문제는 N이 M+K(쿼리수)보다 현저히 커서 초기 트리 구축 시간 비중이 좀 컸던 것 같지만,
생각보다 차이가 크므로 init 함수 쓰는걸 습관 들이는 것도 나쁘지 않겠다.

핵심 요약 정리

  • 구간 쿼리와 갱신의 시간복잡도 = O(logN), 즉 M개 쿼리의 총 시간복잡도 = (MlogN)
  • 갱신을 하면서 구간 쿼리를 구해야 하는 문제에 주로 쓰인다.
  • 완전 이진 트리 구조이며 크기는 보통 4*N으로 넉넉하게 잡는다.
    • 리프 노드에는 배열 값(초기 값)이 들어가 있다.
    • 그 외 노드에는 구간 합과 같은 구간에 대해 구하고자 하는 값이 담겨있다. ex) [1~4] 범위의 합
    • 부모 노드의 값 = 왼쪽 자식의 값 + 오른쪽 자식의 값 ⇒ tree[node] = tree[node * 2] + tree[node * 2 + 1]
    • 만약 구간의 곱을 구한다고 하면 + 연산이 * 연산으로 변하게 된다⇒ tree[node] = tree[node * 2] * tree[node * 2 + 1]
  • init, update, query 총 세 개의 함수 구현 (init은 필수 아님)
  • node는 무조건 1부터 시작

추가 응용

추가로 응용되는 알고리즘들이 많은데 우선 간략하게만 정리해봤습니다.

하나하나 정리하면 글이 너무 길어져서 하나씩 따로 글을 작성할 예정입니다.

그래서 우선 제가 보고 공부했던 블로그 링크를 올려둡니다.

  • K번째 원소 구하기
  • Lazy propagation
    • 구간 갱신을 빠르게 ⇒ O(logN)O(logN)
    • 필요한 갱신만 바로 하고 급하지 않은 갱신 값은 저장해둔다. 그리고 다음에 갱신할 때 lazy값을 보고 갱신해줌으로써 시간을 단축한다.
    • 즉, “갱신을 미룬다”는 개념을 기본으로 가지고 있다.
    • 원래라면 범위의 N개의 갱신을 모두 해줘야 하지만 이를 구간 갱신 한 번으로 끝난다.
    • O(NlogN)O(NlogN) ⇒ O(logN)O(logN)으로 단축
    • 기본 세그먼트 트리와 갱신 부분만 다르다.
    • 구간 값을 갱신하기 위해서는 범위 연산을 해줘야 하기 때문에 diff * (end-start+1); 와 같이 범위 값이 연산에 들어가 줘야 한다.
      그래서 연산이 단순 사칙연산이 아니라 XOR 연산 처럼 복잡해지면 구간 연산이 복잡해지기 때문에 문제가 어려워진다.
    • 아래 블로그에서 소개하는 “수열과 쿼리 21” 풀이 방법은 Lazy 알고리즘을 사용하지 않고 세그트리를 살짝 변형해서 Lazy 문제를 풀 수 있는 방법이다. lazy 정석 풀이는 아니다.
      처음 보는 풀이고 알아두면 좋을 것 같은 신박한 풀이라 가져왔다.
    • ※ https://anz1217.tistory.com/37
  • 머지 소트 트리
  • 펜윅트리
  • 심화

Reference

profile
beegle
배운 내용을 이해하기 쉽게 다시 정리하는 공간입니다.
다음 포스트

[JAVA] 트리맵의 모든 것 (TreeMap)

1개의 댓글

comment-user-thumbnail
하비
2025년 1월 19일

Wow! 너무 잘 정리되어 있네요 읽으면서 감탄했습니다👍👍 게다가 세그먼트 시뮬레이션 사이트가 있었다니.... 지금껏 아이패드로 그려왔던 저에게 좋은 정보네요

답글 달기