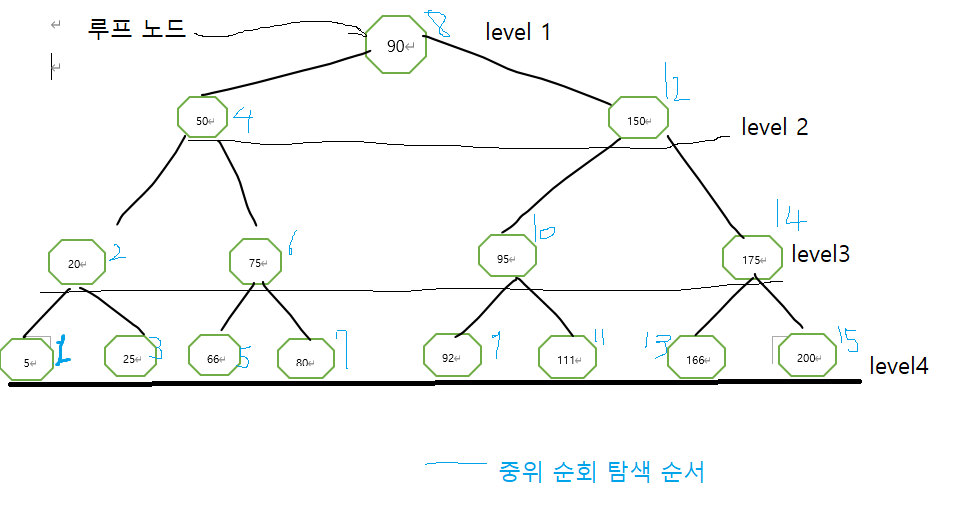
노드
루프 노드- 레벨1에 달린노드
단말 노드 -자식이 없는 맨 마지막에 달린 노드
KEY,
DATA로 나뉨
데이터를 넣을땐 key,data를 가진 pair를 넣는다.
찾을 때는 key를 매개변수로 넣어서
같은 key가 있다면 data가 반환되는 형식으로 탐색이 진행.
찾지 못한다면 end ierator 반환.
Level
각 층을 레벨이라 하고 , 1층 부터 내려간다.
이진 트리
이진트리 자식개수가 2개 이하인 것
완전 이진트리 -자식을 2개로 채우면서 레벨 증가(배열로 구현)-힙에서 구현
자식은 left child,right child 로 나뉨
보통 left child는 부모보다 키 값이 작은것,
rightchild는 부모보다 키 값이 큰것으로 정렬
이진 탐색 트리
이진 탐색: 업앤 다운 게임을 통해 찾고자 하는 데이터를 찾아감 (찾을 때 까지 절반 날리기)
조건(중요!!!)->데이터가 정렬 되어 있어야 함
특징
탐색 횟수 : O(log N) -빅오 표기
데이터 넣을 때 비교 횟수 :O(log N)
탐색 과정에서 큰 효율을 가질 수 있다.
찾아야 하는 데이터에서 한번 계산후 그 데이터가 반씩 줄어들기 때문
순회 종류
전위 순회(pre order): 부모 ->left child->right child
중위 순회(in order): left child ->부모-> right child
후위 순회(post order): left child ->right child->부모
레벨 순회: 1레벨부터 각 레벨로 차례로 순회,QUE 자료구조로 많이 나타 냄(선입선출)
보통 중위 순회를 많이 사용
주의
데이터 입력이 순차적일 때 계속 한 방향으로만 자식이 생성
(탐색을 해도 찾아야 하는 데이터가 절반으로 줄어지지 않음)
해결->균형을 잡아야 함
자가균형
Self balanced BST 자가균형 이진 탐색 트리(RED_BLACK , AVL,-자가 균형 알고리즘)
map, set(레드블랙 자가 균형)
map 구현
헤드가 같으면 들어올 때 마다 주렁 주렁 달아놓음
인설트와 탐색 유사한 구조
탐색: 찾다가 없으면 END ITERATOR 반환
++중위 순회 기준으로 가야함
GETINORDER SUCCESSOR (중위 후속자)- 해당 노드를 기준으로 다음 탐색 노드
GETINORDER PREDCESSOR(중위 선행자)- 해당 노드를 기준으로 탐색한 이전 노드
Insert의 중요
크기 비교후 비교 기준의 자식 자리가 비워있으면 그자리가 내자리다
Search의 중요
자식이 없을 때 자기가 오른 자식이면 현재 헤드보다 큰 헤드를 가진 부모까지 올라간다.
자식이 없을 때 자기가 왼 자식이면 부모로 한번 올라간다