[TIL] #1.2.3 Confidence Interval

ANOVA

여러개의 그룹 한꺼번에 비교

numpy

참고

scipy

from scipy.stats import f_oneway

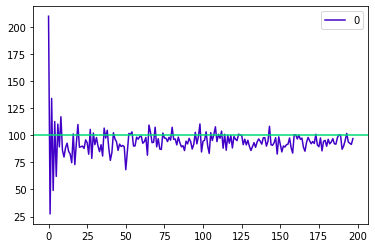
f_oneway(x, y, z)

참고

큰 수의 법칙 (Law of large numbers)

sample 데이터의 수가 커질 수록, sample의 통계치는 점점 모집단의 모수와 같아진다.

Method Chaining

메서드가 객체를 반환하게 되면, 메서드의 반환 값인 객체를 통해 또 다른 함수를 호출할 수 있다.

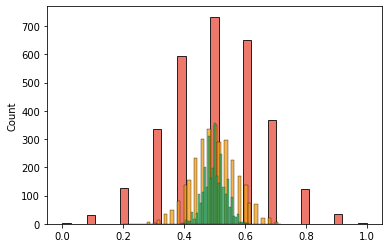
중심극한정리 (CLT)

sample의 데이터가 많아질 수록, sample의 평균은 정규분포에 근사함 형태로 나타난다.

신뢰도 (confidence coefficient)

구간이 100 개, 최소한 모수가 포함된 구간이 95개 있을 경우에 이 구간을 95% 신뢰구간이라고 한다.
좀 더 정확히 말하면 신뢰수준이 95%인 신뢰구간이다.

numpy

from scipy import stats

"""
  표본 평균에 대한 신뢰구간을 계산.
  
  입력 값 : 
    data - 여러 개로 이루어진 (list 혹은 numpy 배열) 표본 관측치
    confidence - 신뢰구간을 위한 신뢰도 
  
  반환 되는 값:
    (하한, 상한구간)으로 이루어진 tuple
  """
  
def confidence_interval(data, confidence=0.95): #신뢰도 95%
    data = np.array(data)
    mean = np.mean(data) #평균
    n = len(data) #표본크기
    std_err = stats.sem(data) #표준오차
    interval = std_err * stats.t.ppf((1 + confidence) / 2, n-1) #ppf : inverse of cdf
    
    return(mean - interval, mean + interval)

scipy

from scipy.stats import t

n = len(sample) #크기
dof = n-1 #자유도
mean = sample.mean() #평균
sample_std = np.std(sample, ddof = 1) #표준편차
std_err = sample_std / n ** 0.5 #표준오차, sample_std / sqrt(n)

CI = t.interval(.95, dof, loc = mean, scale = std_err)

참고