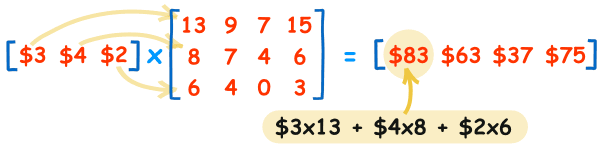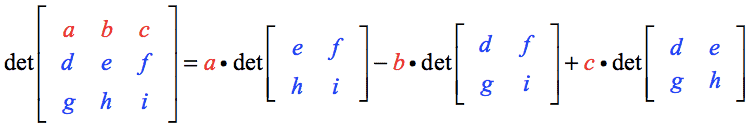[TIL] #1.3.1 Vector / Matrix

Matrix Calculation

Matrix multiplication

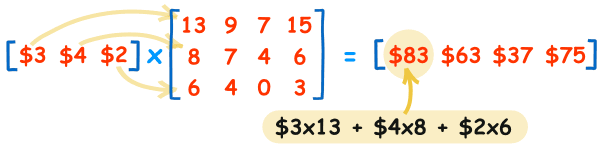
출처

Determinant

2x2

출처

3x3

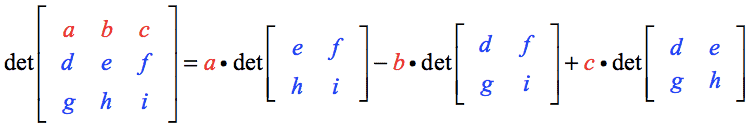
출처

Norm

L1 Norm

벡터의 요소에 대한 절댓값의 합
요소의 값 변화를 정확하게 파악할 수 있음

$L_1 = (\sum_i^n |x_i|) = |x_1| + |x_2| + |x_3| + …. + |x_n|$

L2 Norm

L2 Norm은 n 차원 좌표평면(유클리드 공간)에서의 벡터의 크기를 계산하기 때문에 유클리드 노름(Euclidean norm)이라고도 함

$L_2 = \sqrt {\sum_i^n x_i^2} = \sqrt {x_1^2 + x_2^2 + x_3^2 + …. + x_n^2}$

출처

Evaluation of regression model

Mean squared error, MSE: 평균제곱오차

모델의 예측값 H(Xi)와 실제값 yi의 차이인 오차들의 제곱 평균으로 정의

$MSE := \cfrac{1}{N}\sum_{i=1}^{N}\left (H(X_i) - y_i \right )^2$

Mean absolute error, MAE: 평균절대오차

MSE가 예측값과 실제값의 L2-norm을 사용한 것과 달리 MAE는 오차의 절댓값 평균인 L1-norm을 사용

$MAE := \frac{1}{N}\sum_{i=1}^{N}\left | H(X_i) - y_i \right |$

출처