
Longest Increasing Subsequence
Classic한 문제. 다만 매번 접근 방법을 까먹는 것 같아 기록해보려 한다.
1. Using a classical DP method
왜 DP가 생각이 나야 하는가? -> 선택을 할 지 안할지는 이전 결과에 영향을 받고, 그 결과는 이후의 판단에 영향을 끼치므로, overlapping substructure, optimal substructure 를 가진다고 할 수 있음.
어떤걸 메모할 것인가? -> 내가 원하는 결과를 direct하게 저장하고, 이를 재귀적으로 사용할 수 있어야 한다. 즉 이번의 경우, 각 [0...index]까지의 배열에서 얻을 수 있는 가장 큰 길이의 subsequence 길이를 저장해야한다는 점은 불변.
그렇다면, 적어도 나는 vector<int>를 (nums.size(), 1) 로 초기화 해야한다는 사실까지는 바로 도출해야만 했다.
어떤 방식을 사용할건가(top-down or bottom-up)? -> 가장 basic한 DP의 경우, 해당 element를 선택 하는가, 하지 않는가에 대한 접근 방법이 생각 한다. 이번에도 마찬가지로 접근할 수 있는가? 불가능.
그렇다면? -> sub structure를 생각해보는 거다.
단순히 이전의 memoization으로만 원하는 것을 알기 어려운가? -> 그렇다면 iteration당 더 많은 범위를 서칭해야 하는건가? -> 그렇다면 적어도 2중 for문이 사용될 것인데, 어떤 식으로 구조를 확장해나갈것인가?
여기까지의 생각 이후에는, 어쩌면 자명해진 풀이방법.

각 index에 대한 iteration에서, 전의 모든 memoization (technically, it's a tabulation method) 를 사용해야하고, length만 저장하면 되므로 위와 같이 업데이트를 할 수 있을 터.
2. Using a binary search
여기서 binary search를 떠올릴 수 있는 근거가 뭐냐 도대체? -> '적어도' 오름 차순으로 이루어진 subsequence를 찾는 것 = 해답이 될 수 있는 어떤 array는 오름차순으로 구성이 될 것. 즉, 정렬된 배열에 대한 search 이므로...
(근데 나는 "정렬이 되지 않은 배열에서" 정렬된 구조를 찾아야 하는 문제였기에, 이를 바로 떠올리는 것은 쉽지 않은 접근 방법)
아무튼, Binary search를 어떻게 사용할 수 있는데?에 앞서, 내가 구해야 하는 답은, 증가하는 숫자로 이루어진 배열의 길이 임을 알 수 있음.
[2,6,8,3,4,5,1]이라는 배열에 대하여 생각을 해볼 때,
맨 처음에는 [2], 그리고서는 [2,6], 그리고 [2,6,8] 까지는 아주 자명하다.
그러나 3을 만나는 경우, 새로운 배열이 3으로 시작해서 더 커질 수도, 혹은 2에서 시작해서 3을 포함할 수도, 혹은 3에서 배열이 끝나 [2,6,8] 기존 배열이 제일 길 수도 있기 때문에, 어떤것도 확신을 할 수가 없다.
그렇다면 [2, 6, 8], [2, 3] 이런 배열을 일일이 다 만들어서 가져가야 하는가? -> 만약 그렇게 된다면 공간도 공간이고 시간도 시간이고 사실상 불가능한 방법임을 안다.
다만! 이 모든 상황에서 변하지 않는 것은, 2 -> 6 -> 8 다음 3이 왔을 때, 아무튼 간에 maximum length에 대한 해답은 여전히 3이라는 것. 그리고, 결과적으로 3이 longest array를 구성하지 않게 될 수는 있더라도, 포함이 된다고 가정하면, 2는 항상 포함이 될 것이라는 점.
즉, 기존 배열에서 3보다 큰 가장 작은 수를 3으로 대체한다면, 앞서 제시된 모든 가능성을 한번에 커버할 수 있게 된다는 것이다.
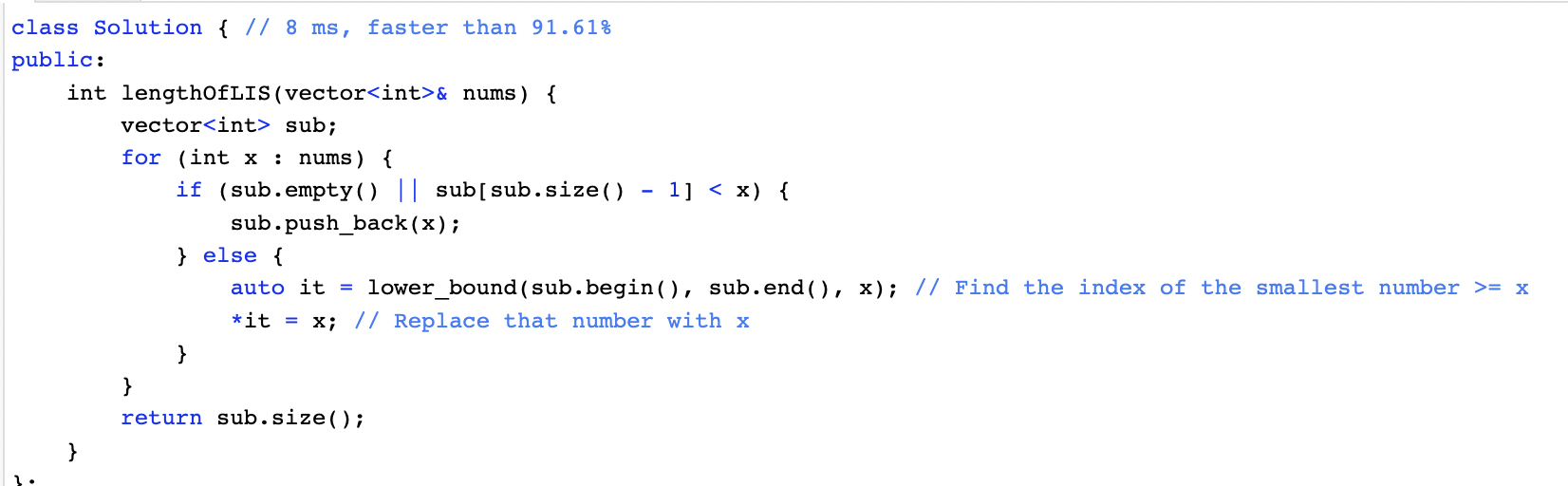
한번의 큰 iteration, 그리고 그 안에서 binary search를 이용한 searching을 이용하여 보다 효율적인 방법으로 해답을 찾아낼 수도 있다는 점.
