[P&R] 0. Set Theory

Definition

"A set" is defined as a collection of elements.

Ex) Tossing a coin twice

• Condition : Coin has two cases, have head or tail

U = {HH, HT, TH, HH} ~ Universal Set (Set of all cases)

A set = {HH, HT} ~ Subset A (Head at the 1st toss case)

B set = {TH, HT} ~ Subset B (Only one Head)

■ Set Operation

• $A ⊂ B$ ~ A is a subset of B
• For any A, $⌀ ⊂ A$, $⌀ ⊂ ⌀$, $A ⊂ A$ (A can be subset of A)
• If $A ⊂ B$ and $B ⊂ C$, Then $A ⊂ C$
• $A = B$ if and only if (a.k.a iff) $A ⊂ B$ and $B ⊂ A$
• Union ~ $A ∪ B$ (It called A cup B) ≈ $A + B$ ( A or B)
• Intersection ~ $A ∩ B$ ≈ $AB$

[Reference]

• $A ∪ B$ has commutative and associative law
• $A ∩ B$ has commutative, associative, distributive law

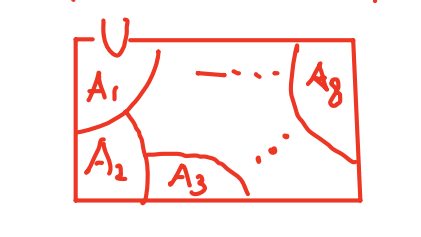
■ Mutually Exclusive Sets

• Sets A and B are said to be mutually exclusive iff $Ab = ⌀$
• Sets $A_1, A_2, A_3, .... , A_n$ are said to be mutually exclusive iff not have intersection

  • $A_iA_j = ⌀, ⩝ i ≠ j$

  

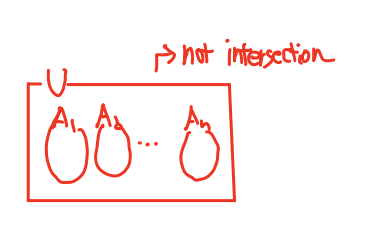
■ Partition

• Partition S of a set U is a collection of sets {$A_1, A_2, A_3, ....., A_n$}

• $A_1 ∪ A_2 ∪ A_3 ∪ ... ∪ A_n = U$

• $A_iA_j = ⌀, ⩝ i ≠ j$

■ Complements of $A$ ~ $A^c$

• $A ∪ A^c = U$
• $AA^c = ⌀$ ( $∵ A$ and $A^c$ are partiion of U)
• $(A^c)^c$ = A
• $U^c = ⌀$
• $⌀^c = U$

■ DeMorgan's Law

• $(A ∪ B)^c = A^c ∩ B^c$
• $(A ∩ B)^c = A^c ∪ B^c$

본 글은 HGU 2023-2 확률변수론 이준용 교수님의 수업 필기 내용을 요약한 글입니다.