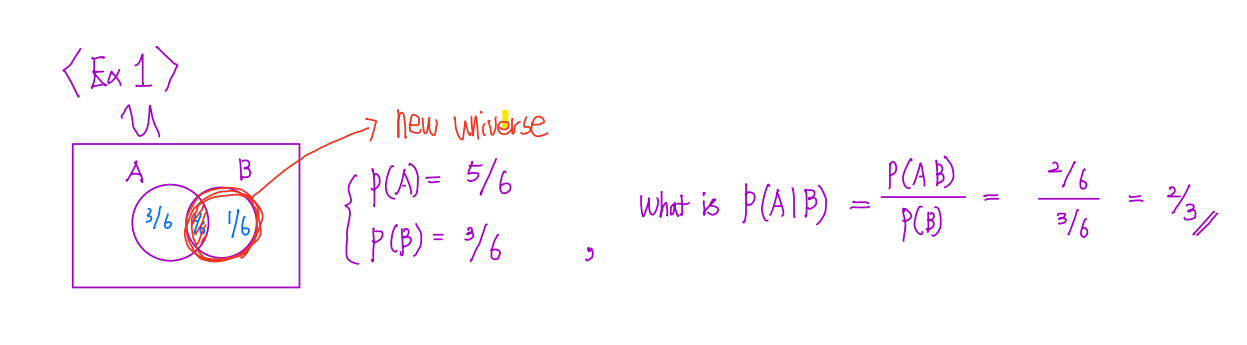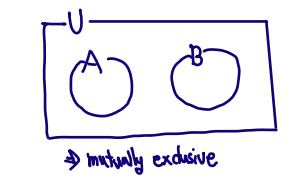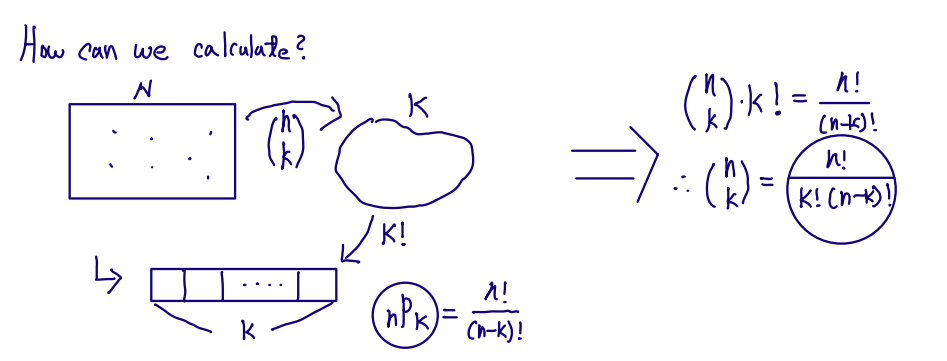[P&R] 01. Probability

■ Axomic Definition of Probability

• Axiom(공리) : Some statements or facts that we accept it as the truth.

  e.g. Die experiment

  • $U =\{1, 2, 3, 4, 5, 6\}$ ~ "Sample Space"
  • Each point called outcome or sample point

⭐ Sample Space : A collection of all sample points of a random experiment

⭐ event : A subset of the sample space

---

■ Probability axioms

• $P(A) \ge 0$
• $P(U) = 1$
• If $AB = \phi,$ $P(A \cup B) = P(A) + P(B)$

⭐ Probability is assined to "Event"

---

■ Properties of probability

1. $P(\phi) = 0$
2. $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
3. $P(A^c) = 1 - P(A)$
4. $If$ $\{A_1, A_2, \cdots, A_n\}$ is a sequence of mutually exclusive events, $P( \bigcup_{i=1}^n Ai) = \sum_{i=1}^{n} P(A_i)$

---

■ Conditional Probability

• Definition : The conditional probability of event A, given B is defined as.

$P(A | B) = \frac{P(AB)}{P(B)} \Leftrightarrow P(B|A) \times \frac{P(A)}{P(B)}$
$P(AB) = P(A|B) \times P(B) \rightarrow$ This expression is more comfortable than above equation.
( $∵ P(B)$ can be 0)

✏️ Exercise 1

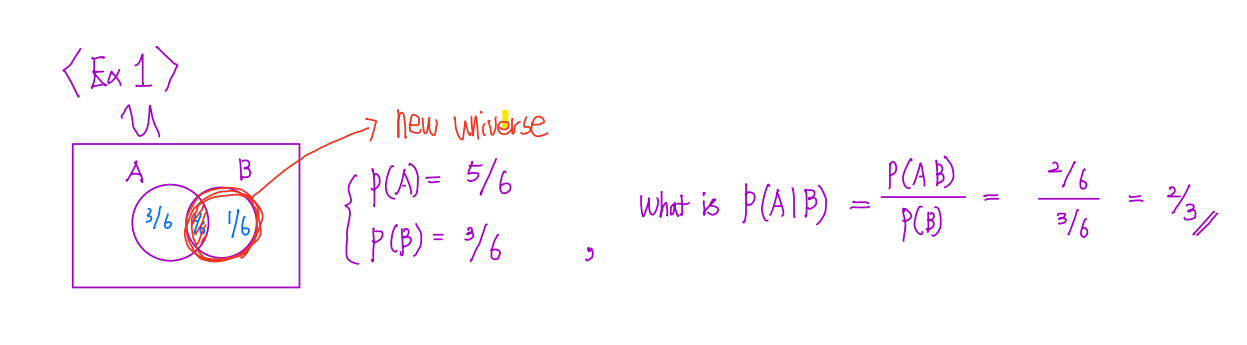
✏️ Exercise 2 & 3

---

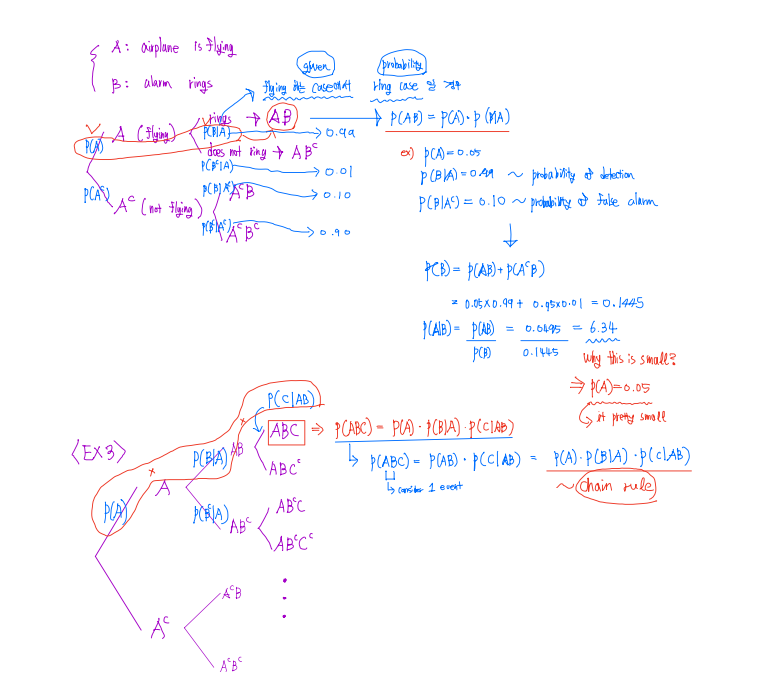
■ ⭐ Total Probability Theorem ⭐

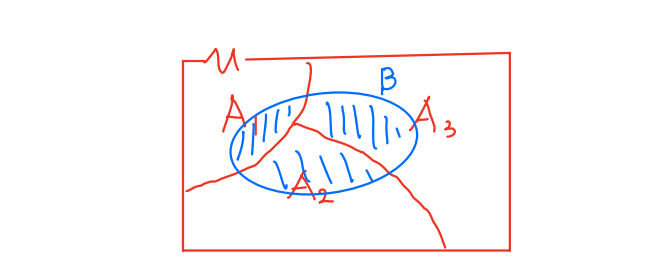
$\{A_1, A_2, A_3\}$ ~ partion of U
$P(B) = P(A_1B) + P(A_2B) + P(A_3B)$
$\Leftrightarrow P(A_1) \times P(B|A_1) + P(A_2) \times P(B|A_2) + P(A_3) \times P(B|A_3)$
$∴ \sum_{i=1}^{3} P(B|A_i)\times P(A_i)$

In genral, $P(B) = \sum_{i=1}^{n} P(B|A_i) \times P(A_n)$ ~ Total Probability Theorem

---

■ Baye's Rule

• This rule focus on calculationg below thing.

$P(A_i | B) = ?$
$P(A_i)$ ~ Prior prbability ~ initial believe (It means occurs A it self, not related to B)
$P(A_i | B) = \frac{P(B|A_i) \times \frac{P(A_i)}{P(B)}}{P(B)}$ $(P(B) = \sum_{i=1}^{n} P(B|A_i) \times P(A_n))$

---

Example

(a) What is the probability that the picked one is defective?

Solution)

$P(D) = \sum_{i=1}^{4} P(D|B_i) \times P(B_i)$
       $= 1/4 \times (0.05 + 0.4 + 0.1 +0.1)$
$∴$ $0.1625$

(b) If the picked one is defective, what is the probability that it came from Box2?

Solution)

$P(B_2|D) = \frac{P(D|B_2) \times P(B_2)}{P(D)}$
           $= \frac{(0.4) \times (0.25)}{0.1625}$
$∴$ $0.6154$

---

■ Independence

• Two events A and B are said to be independence iff
  $\rightarrow$ Whether or not occur event B, probability A is not changed

  $P(A|B) = P(A)$
  $\Leftrightarrow P(B|A) = P(B)$
  $\Leftrightarrow P(AB) = P(A)\times P(B)$

🚨 Question

If $P(A) \ne 0$ and $P(B) \ne 0$, Can these two events be both independent and mutually exclusive?

Answer : NO!!

$P(AB) = P(A) \times P(B)$

In this case, $P(AB) = 0$, $(P(A) = P(B)) \ne 0$

It is not make sense...! Because according to the independence,

It should be $P(AB) = P(A) \times P(B)$

---

■ Conditional Independence

✏️ Example

• Consider two unfair coins A and B
• Choose a coin and toss it twice
• $P(head | A) = 0.9$ and $P(head|B) = 0.1$
• $H_1 =$ $\{$ First toss is head $\}$ and $H_2 =$ $\{$ Second toss is head $\}$

(a) Once we know it is coin $A$, are $H_1$ and $H_2$ independent ?

📋Solution

$P(H_1H_2 | A) = P(H_1|A) \times P(H_2|A)$
$\Leftrightarrow 0.9\times0.9 = 0.9 \times 0.9$
$∴ H_1$ and $H_2$ are conditional independent

(b) If we don't know which coin it is, are $H_1$ and $H_2$ independent ?

📋Solution

$P(H_1H_2) = P(H_1) \times P(H_2)$
$P(H_1) = P(H_1|A) \times P(A) + P(H_1|B) \times P(B)$
$\Leftrightarrow \frac{1}{2} \times (0.9 +0.1)$
$\Leftrightarrow \frac{1}{2}$
Same progress $P(H_2)$
However, $P(H_1H_2) = P(H_1H_2 | A)\times P(A) + P(H_1H_2 | B) \times P(B)$
$\Leftrightarrow (0.9 \times 0.9 \times 0.5) + (0.1 \times 0.1 \times 0.5) = 0.41 \ne P(H_1)\times(H_2)$
$∴H_1$ and $H_2$ are dependent

---

■ Independence of Collection of Events

• Events $A_1, A_2, \cdots, A_n$ are said to be independent iff
  for any set of distinct index $I\subset \{1, 2, \cdots , n\}$

  $P \bigg( \bigcap_{i\in I} A_i \bigg) = \prod_{i\in I} P(A_i)$

Is this necessary-sufficeint condition? => NO, necessary condition.

<cf> Any Set must be express to the product of each of probability

---

---

■ Pairwise Independence

• Events $A_1, A_2, \cdots, A_n$ are said to be pairwise independent iff

  $P(A_iA_j) = P(A_i)\times P(A_j)$$,$ $\forall i \ne j$ $($Any pair must be satisfied$)$

✏️ Example

• $A = \{$First toss is head$\} \rightarrow P(A) = 1/2$
• $B = \{$Second toss is head$\} \rightarrow P(B) = 1/2$
• $C = \{$First and second toss give the same result$\} \rightarrow P(C) = 1/2$

What we want to do$...$
1. Determined that 3 events are independent or not.
2. Determined that 3 events are Pairwise events or not.

• $P(AB) = P(BC) =P(CA) = \frac{1}{4}$
• $P(ABC) = \frac{1}{4} \ne P(A)\times P(B)\times P(C)$
  $∴$ Pairwise independence does not imply independence!
  But! Independence can imply the Pairwise independence!

---

■ Counting Principle

• Experiment consisting of r stages
• $\exists n_i$ choices at stage $i$
• Number of choices = $n_1 \times n_2 \times \cdots \times n_r$

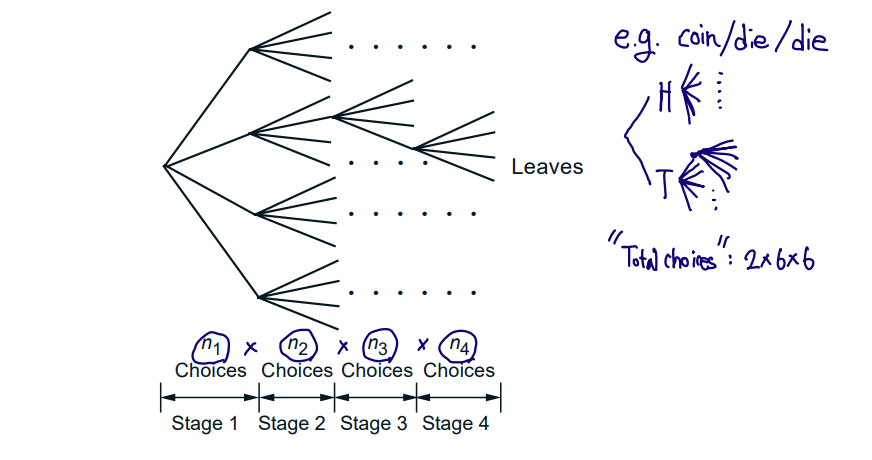
✏️ Example

$1)$ Number of license paltes (e.g. HGU0387)

📋Solution

• # Alphabetical number: 26
• # Integer number: 10
  $∴ 26 \times 26 \times 26 \times 10 \times 10 \times 10 \times 10$

$2)$ Number of subsets of an $n$-element set

📋Solution

[ EX ]
$\{1, 2, 3, 4\} \rightarrow \{1\}, \{1, 2, 3\}, \cdots$
Binary Decision: $2\times 2\times 2\times 2 = 2^4$
We can see the pattern when we use 'Binary Decision'
$∴n$-$element \rightarrow 2^n$

---

■ Permunations

• K-permutations: Number of ways of picking k out of n objects and arrange them in a sequence

$(1)$ $nC$k $\times k! = \frac{n\times (n-1) \times \cdots \times (n-k+1)}{k!} \times k!$
$(2)$ Choose $k$ and arrange in $\{1, 2, 3, \cdots, n\} \rightarrow \frac{n!}{(n-k)!} = nP$ =k

---

■ Combinations

• Number of $k$-element subsets of a given $n$-element set that no ordering of the selected elements
• $n \choose k$$= nC_k$ : "$n$ choose $k$"

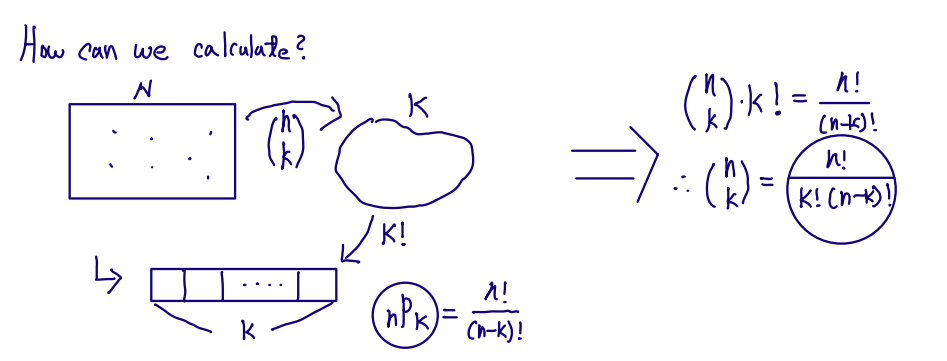
$<$Conference$>$

"Binomial coefficients"

$E$x$) \sum_{k=0}^{n}$$n \choose k$ $=$$n \choose 0$ $+$ $n \choose 1$ $+$ $\cdots +$ $n \choose n$ $= 2^n = (nC_0 +\cdots+nCn)$
It means that we choose the elements true or fals.
Therefore, each element have 2 choices, total cases are $2^n$

---

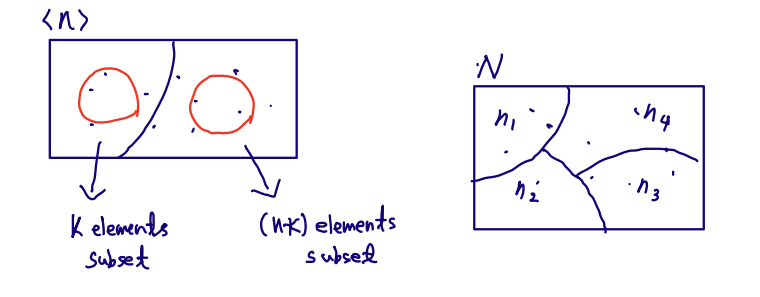
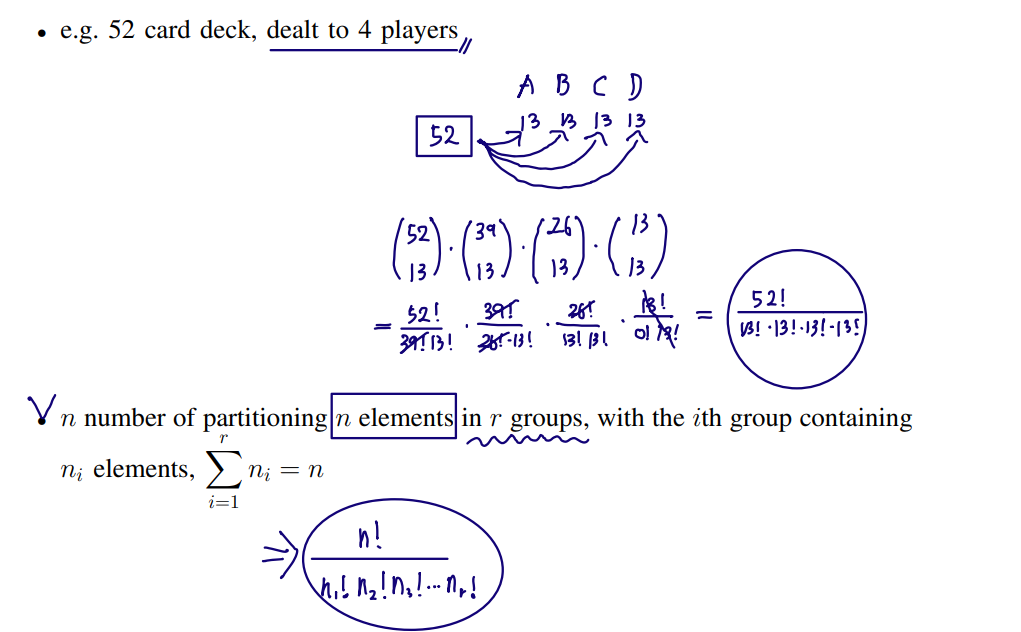
■ Partitions

---

■ Bernoulli Trials

Let A be an event in a random experiment with $P(A) = p$ and $P(A^c) = 1-p$
Repeating this experiment n times, probability that A occurs k times in any order is calculated by.....

$P_n(k)$ = $n \choose k$ $\times p^k \times (1-p)^{n-k}$ ~ "Binomial Probability"

$e.g.$ We toss 5 coins independently

• $P(H) = p$, $P(T) = 1-p$
• $P(HHHTT) = p \times p \times p \times (1-p)^2$
• $P($ 3 heads and 2 tails in any order $)$ = ???

---

■ Generalization

Let $[A_1, A_2, \cdots, A_r]$ be a partition of $U$. Let $P(A_i) = p_i,$ $\sum_{i=1}^{r}$$p_i = 1,$ and $\sum_{i=1}^{r}$$k_i = n.$

Then,
$P_n$$(k_1, k_2, \cdots, k_r) =$ $\frac{n!}{k_1!\times k_2! \times \cdots \times k_r!}$ $\times (P_1)^{k_1} \times (P_2)^{k_2}\times \cdots \times(P_r)^{k_r}$

---

본 글은 HGU 2023-2 확률변수론 이준용 교수님의 수업 필기 내용을 요약한 글입니다.