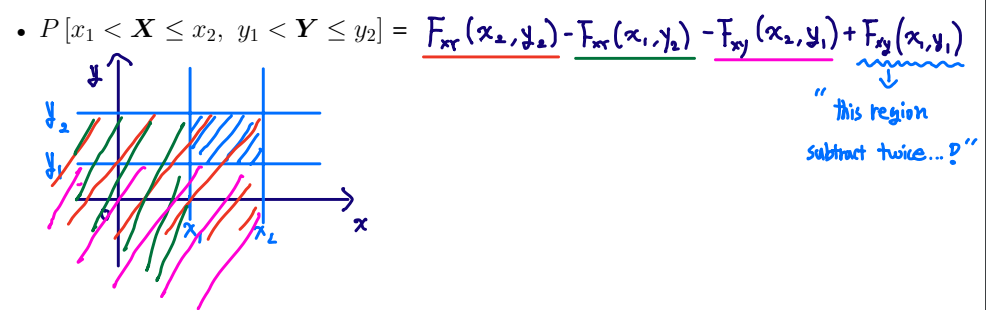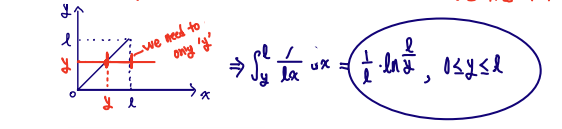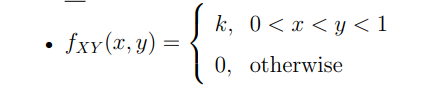■ Joint Density & Distribution
- Joint statistics simply means the statistics of two or more random variables.
- In the discussion of joint statistics, we are interested in the intersection of events.
■ Joint PMF (In 1 random variable, PX(x)=P[X=x])
-
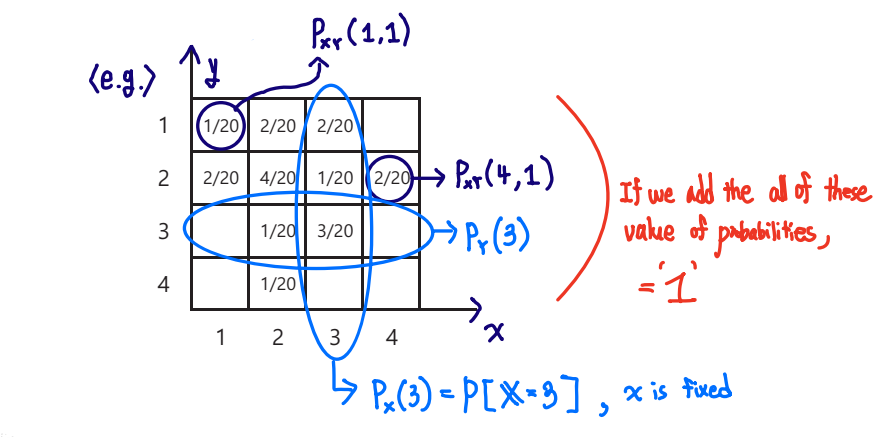
PXY(x,y)=P[X=x,Y=y]
-
∑x∑yPXY(x,y)=1
-
PX(x)=∑yPXY(x,y)
-
PY(y)=∑xPXY(x,y)
-
PX∣Y(x∣y)=P[X=x∣Y=y]=P(Y=y)P(X=x,Y=y)=PY(y)PXY(x,y)
-
∑xPX∣Y(x,y)=∑xPY(y)PXY(x,y)=PY(y)1×∑xPXY(x,y)=1 (∵∑xPXY(x,y)=PY(y))
■ Joint PDF ~ fXY(x,y)
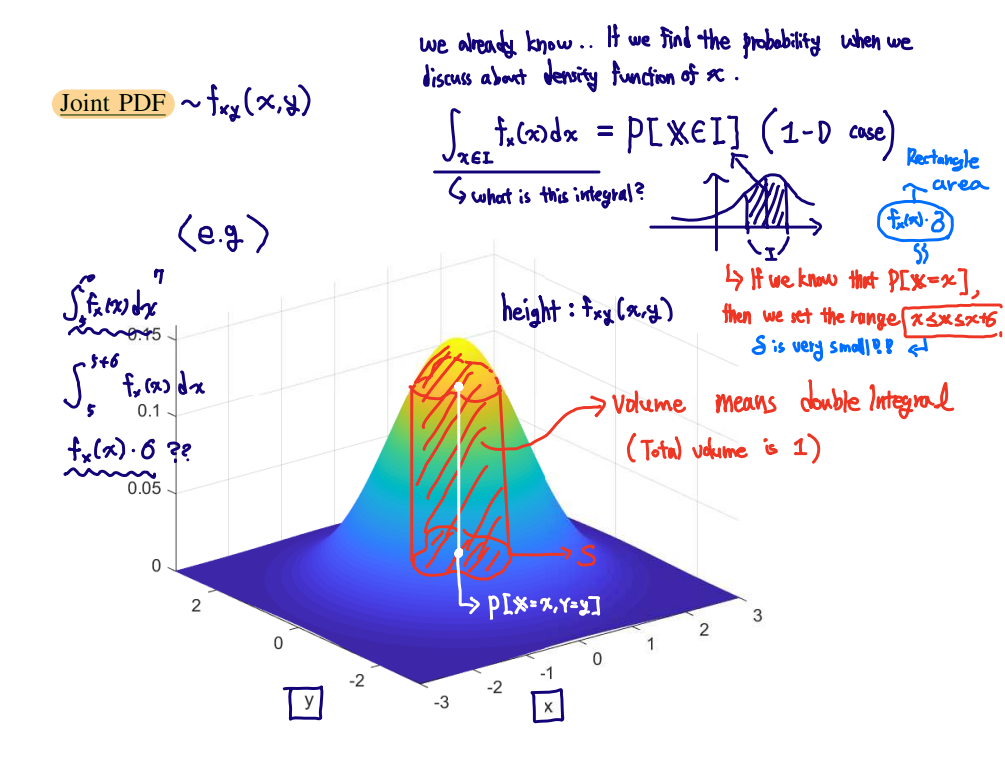
- P[(X,Y)∈S]=∫∫(x,y)∈IfXY(x,y) dxdy
- ∫−∞∞∫−∞∞fXY(x,y) dxdy
- P[x≤X≤x+δ,y≤Y≤y+δ]≈P[X=x,Y=y]≈fXY(x,y)×δ2
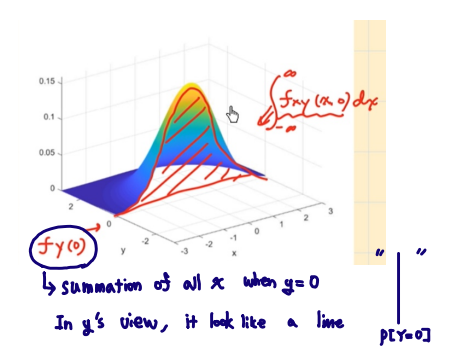
- fX(x)=∫−∞∞fXY(x,y) dy
- fY(y)=∫−∞∞fXY(x,y) dx
■ Joint Distribution
- Joint distribution of random variables X and Y is defined as fXY(x,y)=δxδyδ2FXY(x,y)
FXY(x,y)=P{X≤x,Y≤y}
■ Properties
- FXY(−∞,y)=P{X≤−∞,Y≤y}=0
FXY(x,−∞)=P{X≤−∞,Y≤y}=0
FXY(∞,∞)=P{X≤−∞,Y≤y}=1
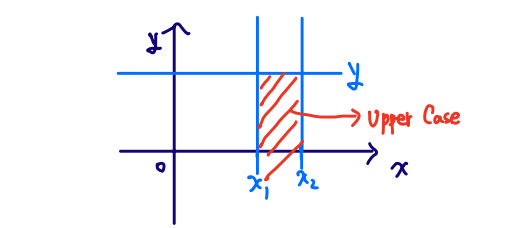
- Assume that x2>x1, FXY(x2,y)−FXY(x1,y)=P{x1≤X≤x2, Y≤y}
- Assume that y2>y1, FXY(x,y2)−FXY(x,y1)=P{X≤x, y1≤Y≤y2}
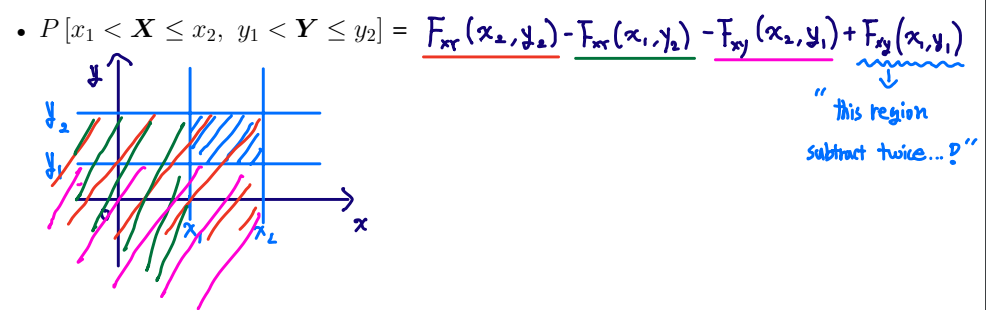
- fXY(x,y)=dxdydFXY(x,y)
- FXY(x,y)=∫−∞x∫−∞yfXY(α,β)dαdβ
- In comparison with joint distiribution (or joint density), the distribution of each random variable is called "marginal distribution (or density)."
- FX(x)=P{X≤x}=P{X≤x,y≤∞}=FXY(x,∞)
- FY(y)=FXY(∞,y)
- fX(x)=∫−∞∞fXY(x,y) dy
- fY(y)=∫−∞∞fXY(x,y) dx

■ Independent random variables
1) Discrete random variables X,Y,Z are said to be independent iff PXYZ(x,y,z)=PX(x)×PY(y)×PZ(z)
Because "Joint Probability mass function" has to be equal to product of, marginal product of function.
- Also we need to satisfy other condition, PXY(x,y)=PX(x)×PY(y)…
However, we just get a 1 condition(PXYZ(x,y,z)=PX(x)×PY(y)×PZ(z)) -> satisfy the others condition.
Let's suppose ∑ZPXYZ(x,y,z)⇔∑ZPX(x)×PY(y)×PZ(z)⇔PXY(x,y)=PX(x)×PY(y)×∑ZPZ(z) (∑ZPZ(z)=1)
Therefore, It can prove others just as 1 conditions.
2) Continouous random variables X,Y,Z are said to be independent iff
⇔fXYZ(x,y,z)=fX(x)×fY(y)×fZ(z)
⇔FXYZ(x,y,z)=FX(x)×FY(y)×FZ(z)
⇔ Events {u∣X(u)≤x},{u∣Y(u)≤y},{u∣Z(u)≤z}areindependent
Independence of RV X, Y, and Z is exactly same as independence of events {X≤x},{Y≤y},{Z≤z}.
Each of these events is acutally collection of sample points which is satisfied above condition.
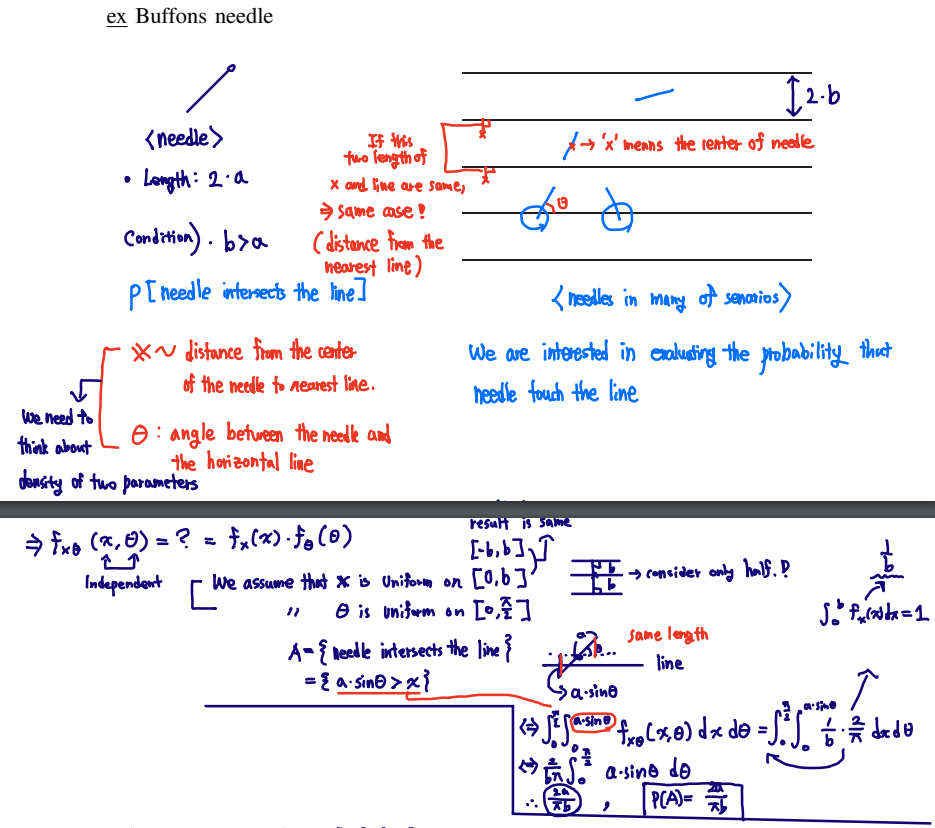
✏️ Buffons needle example
■ Conditioning
Recall that
- PX∣Y(x∣y)=PY(y)PXY(x,y)
- P(x≤X≤x+δ)≈fX(x)×δ
Similarly, let's consider the following probability:
-
P(x≤X≤x+δ∣y≤Y≤y+δ)≈P[y≤Y≤y+δ]P[x≤X≤x+δ,y≤Y≤y+δ]≈fY(y)×δfXY(x,y)×δ2=fY(y)fXY(x,y)×δ
-
fX∣Y(x∣y)=fX∣Y(x∣Y=y)=fY(y)fXY(x,y)
(The difference that above equation is δ.)
-
If X and Y are independent, fX∣Y(x∣y)=fX(x)
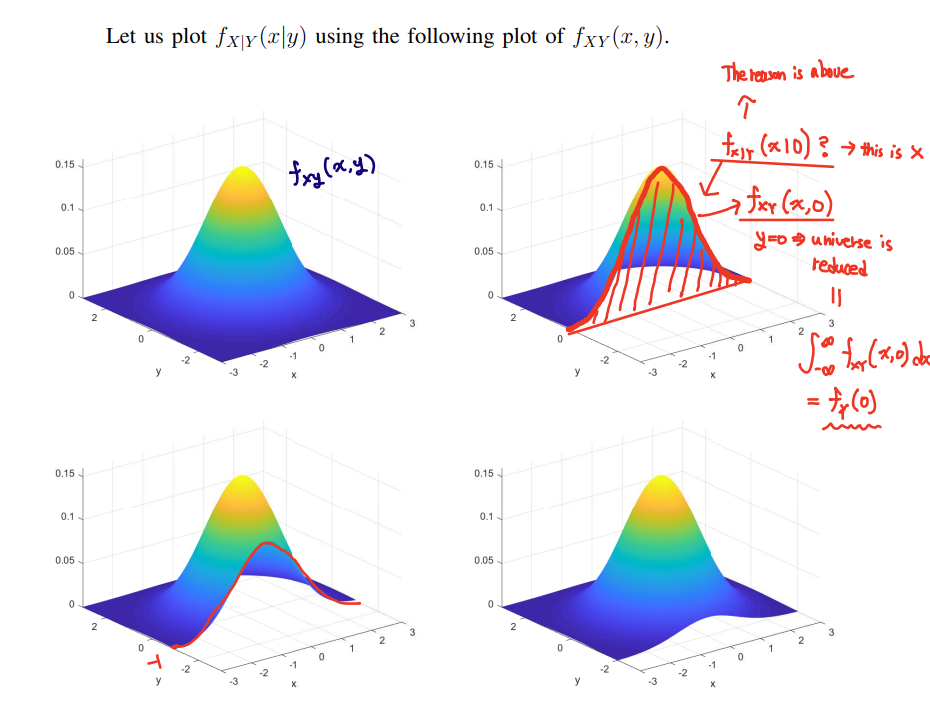
🚨Cf) ∫−∞∞fX∣Y(x∣y) dx=1 is not indicated below pic.

Therefore, it can not be above pic.
Because, according to the y, the result is changed not a 1.
Then, how can we find that density??
⇒ Make an area to 1 using normalization.
fY(0)fXY(x,0)=fX∣Y(x∣0)
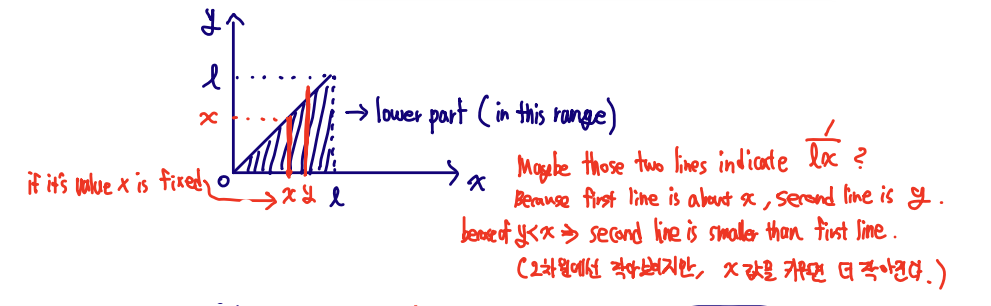
✏️ Stick-breaking example
Assumption
-
Break a stick of length l twice.
-
Break at X which is uniform in [0,l]; then break again at Y whcih is uniform in [0,X]

-
E[Y∣X=x]=x/2 (∵fY∣X(y∣x)'s center of gravity)
-
fXY(x,y)=fY∣X(y∣x)×fX(x)=lx1 ,(0≤y≤x≤l)
-
fY(y)=∫ylfXY(x,y) dx
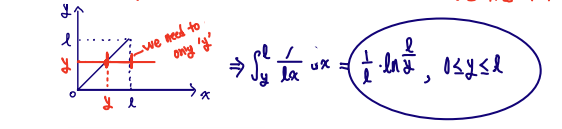
-
fX(x)=∫0xfXY(x,y) dy =∫0xlx1 dy
∴1/l,(0≤x≤l)
-
E[Y]=∫0ly×l1×lnyl dy =4l
✏️ Another example
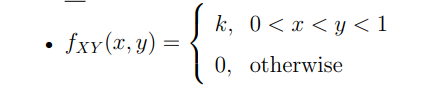
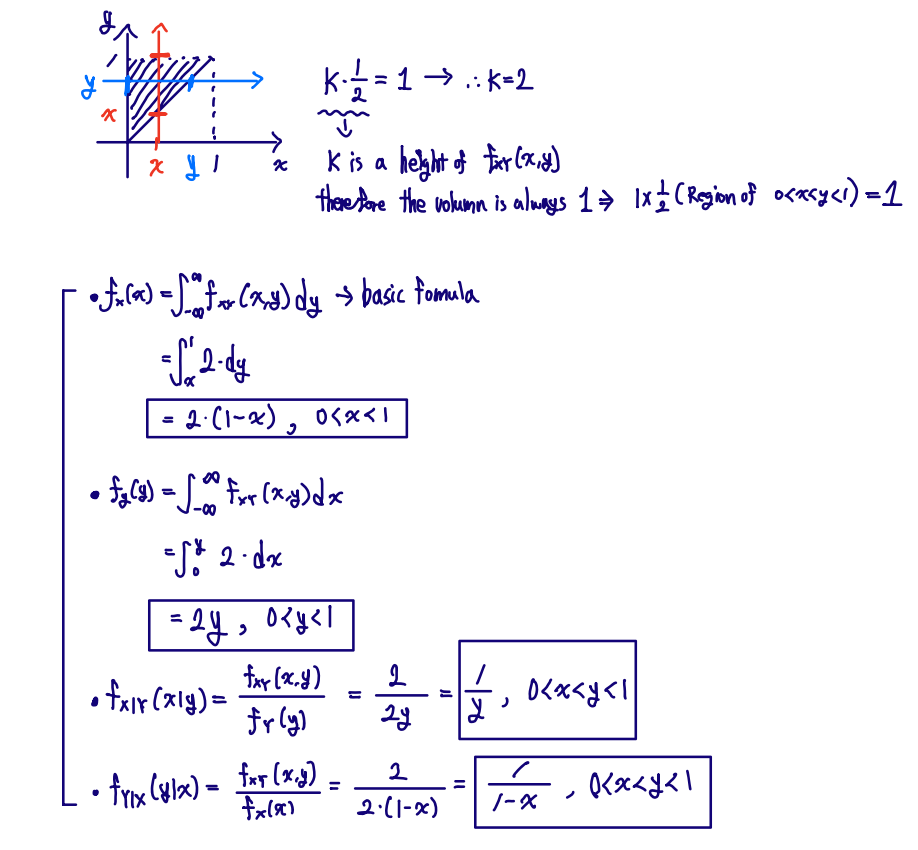
- Determine fY∣X(y∣x) and fX∣Y(x∣y)
■ Expectations
- E[X]=∫−∞∞x×fX(x) dx
- E[g(X)]=∫−∞∞g(x)×fX(x) dx
- E[g(X)∣A]=∫−∞∞g(x)×fX∣A(x∣A) dx
- E[X]=∫−∞∞x∫−∞∞fXY(x,y)dy dx=∫−∞∞∫−∞∞x×fXY(x,y) $dxdy
- E[g(X,Y)]=∫−∞∞∫−∞∞g(X,Y)×fXY(x,y) dxdy
- E[g(X,Y)∣A]=∫−∞∞∫−∞∞g(X,Y)×fXY∣A(x,y∣A) dxdy
- E[X∣Y=y]=∫−∞∞x×fX∣Y(x∣y) dx
- E[X]=∫−∞∞E[X∣Y=y]×fY(y) dy
proof)
E[X]=∫−∞∞x×fX(x) dx
⇔∫−∞∞x∫−∞∞fXY(x,y) dxdy
⇔∫−∞∞∫−∞∞x×fXY(x,y) dxdy
⇔∫−∞∞∫−∞∞x×fX∣Y(x∣y)×fY(y) dxdy
⇔∫−∞∞fY(y)×E[X∣Y=y] dy
We can indicates ∫−∞∞fY(y)×E[X∣Y=y] dy to the g(Y)
Here, E[X∣Y=y] can be regarded as a random variable, being denoted by E[X∣Y]
∴E[X]=E[E[X∣Y]], (Notice that inner expectation is about the X and Outer is about the Y)
✏️ Stick braking example (The range is 0≤y≤x≤l)
We know that E[Y∣X=x]=2x.
And we can assume that E[Y∣X]=g(X)=x/2.
E[Y]=EX[EY[Y∣X]], (we prove this above)
We can easily think E[g(X)]=∫−∞∞g(x)×fx(x) dx.
Therefore, the expansion of above equation, ∫−∞∞2x×fX(x) dx
⇔∫0l2x×l1 dx
∴ l/4
본 글은 HGU 2023-2 확률변수론 이준용 교수님의 수업 필기 내용을 요약한 글입니다.