[자료구조] 배열의 표현 - 1차원배열, 2차원배열, 3차원배열, 다차원배열

✅ 선언과 정의

---

	선언	정의
개념	메모리 상의 주소가 정해지지 않고 이름만 알려줌	대상의 이름에 대해 대응하는 메모리 상의 주소가 정해지는 것
예시	int a; int x( );	int a = 1; int x( ) { return 0; }

• 배열 선언 및 정의

  1. 초기화 프로그램 세그먼트

     int a[100]
     for (int i=0; i<100; i++){
     	a[i];
     }

  2. 심벌상수 이용

     #define N 100
     int a[N]
     for(int i=0; i<N; i++){
     	a[i] = 0;
     }

✅ 1차원 배열

---

• 배열의 선언
  • a[n]
  • a : 배열이름 / n : 원소 최대 수
• 메모리표현
  • 연속적인 메모리 주소를 배열에 할당
  • 원소는 할당된 메모리 내에서 인덱스 순서에 따라 저장
  • 순차사상 : 배열의 논리적 순서와 메모리의 물리적 순서가 같도록 표현
  • 순차표현 : 순차 사상을 이용하여 데이터를 표현

✅ 2차원 배열

---

• 배열의 선언
  • a[n1, n2]
    • n1 : 행(row)의 수
    • n2 : 열(column)의 수
    • 원소 수 : n1 * n2
• 메모리표현
  • 행 우선 순서 (row major order) : 일반적인 방법
  • 열 우선 순서 (column major order)
• 예시

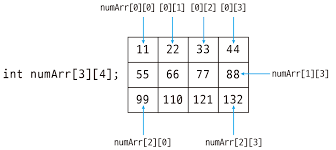
• C의 표현

  int a[2][3] = {1,2,3,4,5,6};
  int a[2][3] = {{1,2,3},{4,5,6}};
  int a[ ][ ] = {{1,2,3},{4,5,6}}; 

✅ 3차원 배열

---

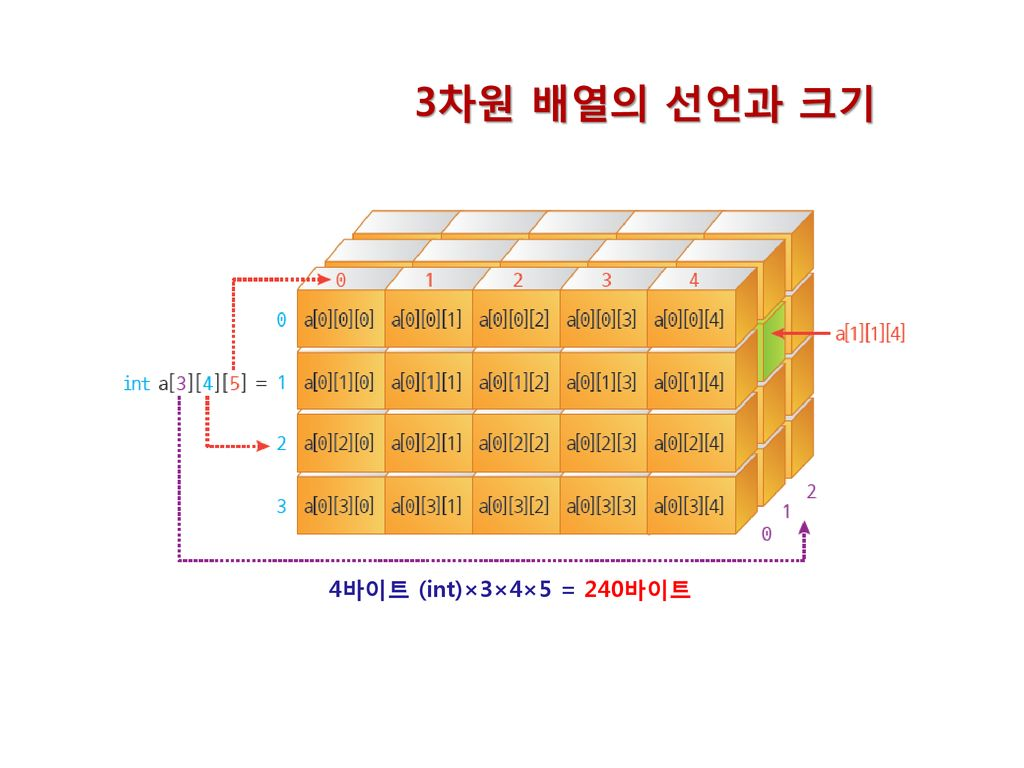
• 배열의 선언
  • a [n1, n2, n3]
    • n1 : 면(plane)의 수
    • n2 : 행(row)의 수
    • n3 : 열(column)의 수
    • 원소 수 : n1 n2 n3
• 메모리 표현
  • n1개의 2차원 배열 (n2 * n3)을 차례로 1차원 메모리에 순차 사상하는 방법
• C 표현

  • int a[3][2][2] = { {{1,2}, {3,4}}, {{5,6}, {7,8}}, {{9,10}, {11,12}} };

• 예시

  variable	memory address	a[4][2][3] 예시 계산
  list [0][0][0]	α (base address)	0
  list [1][1][2]	α +(1 n2 n3) + 1 *n3 + 2	0 + 1(23) + 1*(3) + 2= 11
  list [a][b][c]	α + (a n2 n3) + b *n3 + c	0 + a23 + b*3 + c = 6a + 3b +c

  • a[0,0,0]의 주소가 α라 할 때 a[i1, i2, i3] 주소는 α + i1 n2 n3 + i2 *n3 + i3

✅ 다차원 배열

• 다차원 배열 주소 구하는 방법

  Array A[upper 0][upper 1] ... [upper n-1] 에 대해, α가 A[0][0]...[0]의 주소이면,
  A[i0][i1]...[in-1] = α + i0 • ( upper1 • upper2 ... • upper n-1 )
  
                            + i1 • ( upper2 • upper3 ... • upper n-1 )
  
                            + i2 • ( upper3 • upper4 ... • upper n-1 )
  
                                ...
  
                            + i n-2 • ( upper n-1 )
  
                            + i n-1
  
  - 그러므로,모든aj (0≤j<n-1)를미리구해놓은다음(어떻게?...n-2번의곱셈으로), a[i0][i1]...[in-1] 의 주소를 구해야 할 때, n-1번의 곱셈 (O(n))을 하고, n번의 덧셈으로 a[i0][i1]...[in-1] 의 주소를 구할 수 있다.
  - 최종적인 time complexity: **O(n)**

  
  
• 예시
  • a[x][i][j][k][w] = α + (x u1 u2 u3 u4) + (i u2 u3 u4) + (j u3 u4) + (k u4) + w

✅ structure와 비교

• 배열 : 타입이 같은 데이터의 집합
• 배열 : 타입이 다른 데이터의 집합