희소행렬 추상데이터 타입

✅ Sparse matrix 개념

• 행렬 matrix
  • m개의 행(row)과 n개의 열(colunm)로 구성
  • 2차원 배열에 의한 matrix 표현 ⇒ A [ 6, 6 ]
• 희소행렬 sparse matrix
  • 행렬의 값이 대부분 0인 경우를 가리키는 표현

✅ Sparse matrix 표현

• 2차원 배열을 이용하여 배열의 전체 요소 저장하는 방법
  • 장점 : 행렬의 연산들을 간단하게 구현
  • 단점 : 희소행렬의 경우 많은 메모리 공간 낭비
• 표현 방법
  • 2차원의 경우 (row, col, value) 으로 표현
  • 3차원의 경우 (row, col, depth, value) 으로 표현
  • ex. ( (0, 0, 11) (0, 1, 22) ... (5, 6, 99) ) 으로 표현 (row major 표현방식)

✅ Sparse matrix ADT

• objects
  • <row, column, value>, triple들의 집합
  • row와 column은 정수
• functions
  • for all a,b ∈ Sparse_Matrix/ c ∈ Matrix / u,v ∈ item / i, j, max_col, max_row ∈ index
  • spCreate(max_row, max_col) : return an empty sparse matrix with m * n;
  • spTranspose(a) : return c where where c[j, i]=v when a[i, j]=v;
  • spAdd(a, b) : if (a.dimension = b.dimension) return c where c[i, j]=v+u when a[i, j]=v and b[i, j]=u else return error
    • 덧셈이 되기 위해서는, row와 col의 수가 같아야함. 같지 않으면 error를 반환하는 것
  • spMultiply(a, b) : if (a.numcols=b.num_rows) return c where c[i, j] = sum{k=0}^p (a[i][k] * b[k][j]) , p=a.num_cols else return error;

희소행렬 연산의 C 구현

• ⚠️ 행렬 덧셈, 곱셈 방법
  꼼수학_행렬의 기초연산(덧셈,뺄셈,곱셈)
  

희소행렬 기본 구조체

#defind MAX_TERMS 101 //term의 최대수+1 why? 0번째 통계치를 넣기 위해

typedef struct {
	int row;
	int col;
	int value;
} term;

term a[MAX_TERMS];

희소행렬 배열 표현

index	row	col	value
arr[0]	5	7	9
arr[1]	0	0	11
arr[2]	0	1	22
arr[3]	1	1	33
arr[4]	1	2	44
arr[5]	2	2	55
arr[6]	2	3	66
arr[7]	2	4	77
arr[8]	3	5	88
arr[9]	4	6	99

⚠️ arr[0]에는 행렬의 통계정보를 표현.

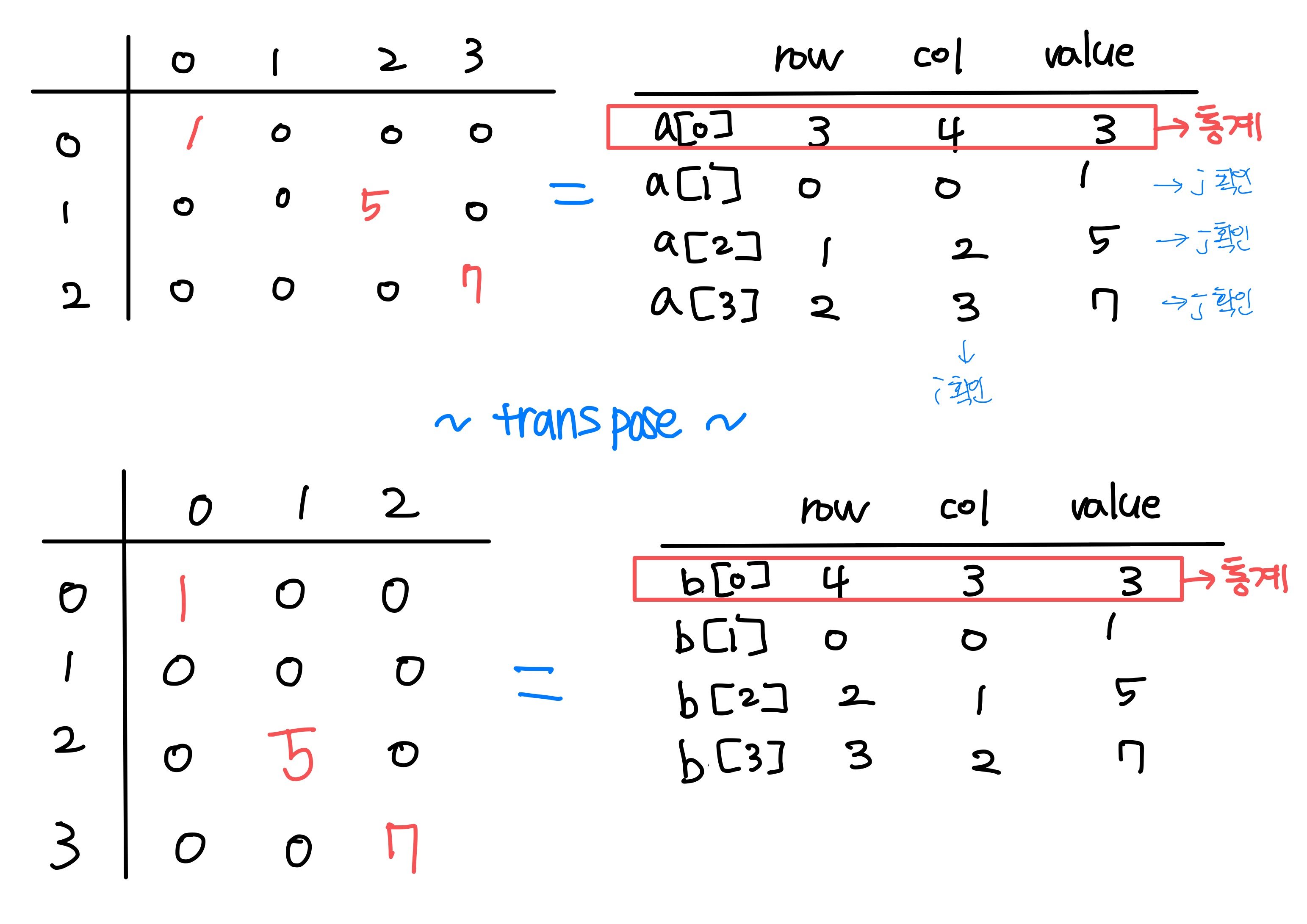
1️⃣ transpose matrix 알고리즘

✅ 개념

✅ 코드

#include <stdio.h>
#define MAX_TERMS 101

typedef struct {
	int row;
	int col;
	int value;
} term;

term a[MAX_TERMS];

void transpose(term a[], term b[]){ //a:원행렬, b:전치행렬
	int n, currentb;
	// 전치행렬 b의 행,열,값 복사 -> b[0] 완성
	n = a[0].value; //총 element수
	b[0].row = a[0].col;
	b[0].col = a[0].row;
	b[0].value = n;
	
	if(n > 0) { // 0이 아닌 원소가 있는 경우에만 전치 연산 수행
		//0번째는 통계량을 가지고 있으므로 1부터 시작
		currentb = 1;

		for(int i=0; i<a[0].col; i++){ //a[0].col 만큼 반복, check의 횟수
			// 0번째틑 통계량이므로 a에 접근하기 위한 j=1부터 시작
			// //0이 아닌 원소 수만큼 반복, write 횟수
			// 값이 있는 만큼(j번) 확인 후에 다시 i로 돌아가 열만큼(i번) 확인

			for(int j=1; j<=n; j++){ 			
				// a.col을 b.row로 정렬하기 위해 0부터 탐색
				// currentb는 b에 데이터가 들어간 인덱스 저장해둠
				// 현재의 열에 속하는 원소가 있으면 b[]에 삽입
				if(a[j].col == i){ 
					// 새로운 데이터 값 정렬
					b[currentb].row = a[j].col;
					b[currentb].col = a[j].row;
					b[currentb].value = a[j].value;
					currentb++;
				}
			}
		}
	}
}

int main(void) {
    // !! a[0]에는 통계값을 집어넣어야 함.
    // a[0]에 들어가는 col과 row는 index가 아닌 갯수로 들어가야함
    term a[4] = { {3,4,3}, {0,0,1}, {1,2,5}, {2,3,7} };
    term b[4];
	
	//원행렬 출력
	printf("row: %d, low: %d, value: %d\n", a[0].row, a[0].col, a[0].value);
	for (int i = 1; i < 4; i++){
    	printf(" %d,  %d,  %d\n", a[i].row, a[i].col, a[i].value);		
	}
    printf("\n\n");
    
	//변형 알고리즘 적용
	transpose(a,b);    
	printf("Transpose processing has been finished.\n");
    printf("\n\n");
    
    //전치행렬 출력
    printf("row: %d, low: %d, value: %d\n", b[0].row, b[0].col, b[0].value);
	for (int i = 1; i < 4; i++){
	    printf(" %d,  %d,  %d\n", b[i].row, b[i].col, b[i].value);	
	}
    printf("\n\n");
    
	return 0;
}

🎯 결과

row: 3, low: 4, value: 3
 0,  0,  1
 1,  2,  5
 2,  3,  7

Transpose processing has been finished.

row: 4, low: 3, value: 3
 0,  0,  1
 2,  1,  5
 3,  2,  7

✅ 시간 복잡도

$O(columns^2 * rows)$

2️⃣ Fast transpose matrix 변형 알고리즘

✅ 개념

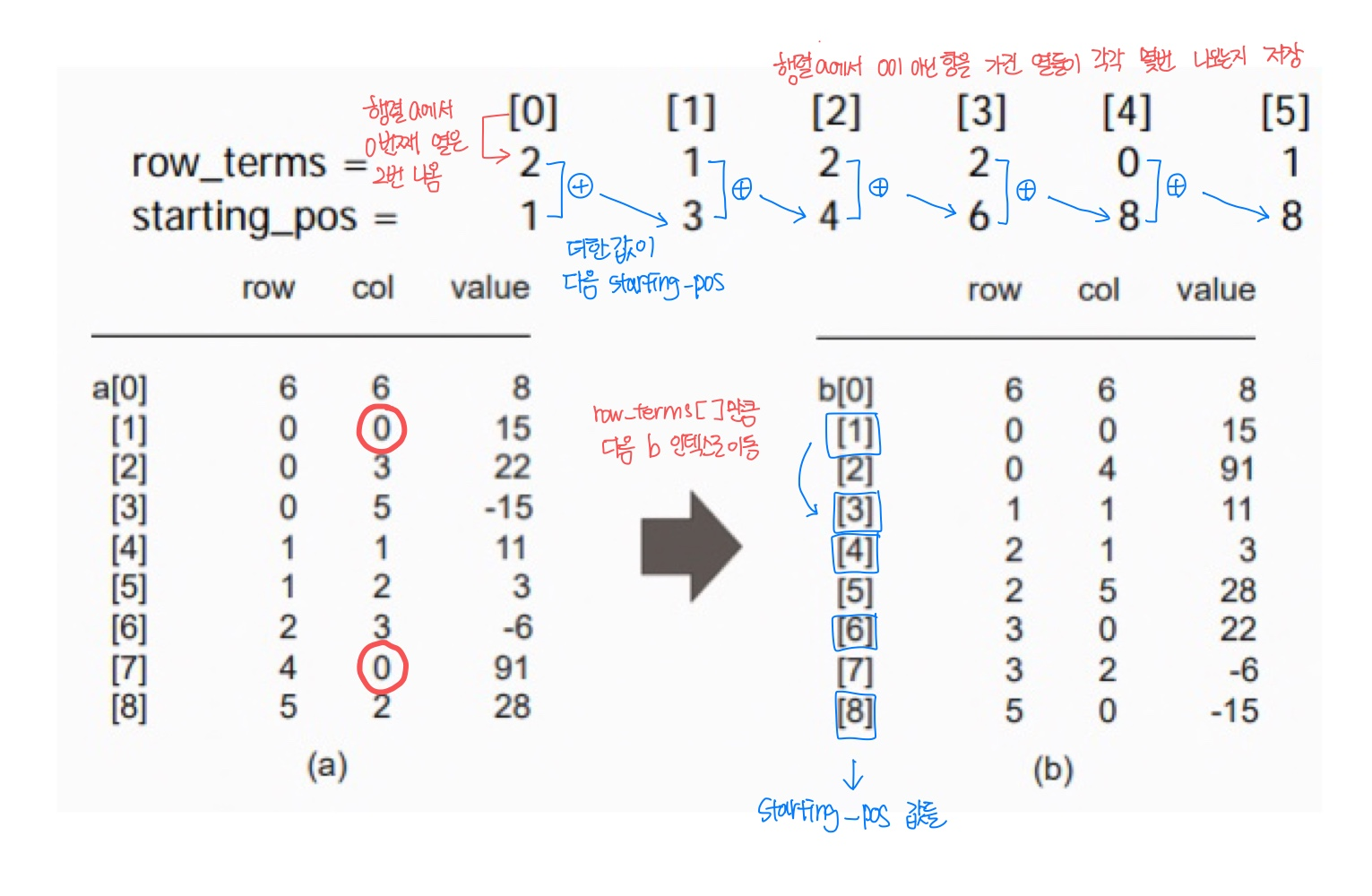
• 각 column이 저장될 곳을 미리 파악하는 방법
  • row_terms : 원 행렬에서, 0이 아닌 값을 가진 열들이, 각각 몇 번 나오는 지 저장
    • index 의미 : 원행렬에서 0이 아닌 값들을 가지고 있는 열의 index
  • starting_pos : 자기 앞 열들이 몇 번 나오는지 저장
    • 원행렬 index에는 row_terms 만큼 값을 가지고 있어 다음 시작하는 열을 알려줌
• column index 저장을 위한 추가적인 공간이 필요
• 메모리에선 이전보다 손해를 보지만 시간 복잡도는 내려가는 효과를 보는 방법

✅ 코드

#include <stdio.h>
#define MAX_TERMS 101
#define MAX_COL 50

typedef struct {
	int row;
	int col;
	int value;
} term;

term a[MAX_TERMS];

void fast_transpose(term a[], term b[]){
    // (1) 필요한 변수 선언
    int i, j;
    int row_terms [MAX_COL], starting_pos [MAX_COL];
    int num_cols = a[0].col, num_terms = a[0].value;

    // (2) a[0]값 b[0]에 복사
    b[0].row = num_cols;
    b[0].col = a[0].row;
    b[0].value = num_terms;

    if ( num_terms > 0 ){
        // (3) row_terms 완성
        // (3-1) col 갯수만큼 row_terms의 배열 0으로 초기화
        // (3-2) col->인덱스로 들어가짐. 인덱스에 해당하는 row_terms 값을 +1 
        for(**i=0; i<num_cols**; i++) row_terms[i] = 0;
        for**(i=1; i<=num_terms**; i++) row_terms[a[i].col]++;

        // (4) starting_pos 완성
        starting_pos[0] = 1;
        for(i=1; i<num_cols; i++){
            starting_pos[i] = starting_pos[i-1] + row_terms[i-1];
        }

        // (5) transpose과정
        for(i=1; i<=num_terms; i++){
            j = starting_pos[a[i].col]++;
            printf("(j = %2d) = (starting_pos[a[%2d].col]++) <= (starting_pos[%d]++)\n", j, i, a[i].col);
            b[j].row = a[i].col;
            b[j].col = a[i].row;
            b[j].value = a[i].value;
        }
        printf("starting_pos : ");
        for (int i = 0; i < 6; i++){
            printf("[%d]", starting_pos[i]);
        }
        printf("\n\n");          
    }      
}

int main(void) {
    // !! a[0]에는 통계값을 집어넣어야 함.
    // a[0]에 들어가는 col과 row는 index가 아닌 갯수로 들어가야함
    term a[9] = { {6,6,8}, {0,0,15}, {0,3,22}, {0,5,-15}, {1,1,11}, {1,2,3}, {2,3,-6}, {4,0,91}, {5,2,28} };
    term b[9];
	
	//원행렬 출력
	printf("index   row   col   value\n");
    printf("--------------------------\n");
	for (int i = 0; i < 9; i++){
    	printf(" a[%d] |  %d     %d     %d\n", i, a[i].row, a[i].col, a[i].value);		
	}
    printf("\n\n");
    
	//변형 알고리즘 적용
	fast_transpose(a,b);
    
    printf("\n\n");
	printf("Transpose processing has been finished.\n");
    printf("\n\n");
    
    //전치행렬 출력
	printf("index   row   col   value\n");
    printf("--------------------------\n");
	for (int i = 0; i < 9; i++){
    	printf(" b[%d] |  %d     %d     %d\n", i, b[i].row, b[i].col, b[i].value);		
	}
    printf("\n\n");  
    
	return 0;
}

🎯 결과

index   row   col   value
--------------------------
 a[0] |  6     6     8
 a[1] |  0     0     15
 a[2] |  0     3     22
 a[3] |  0     5     -15
 a[4] |  1     1     11
 a[5] |  1     2     3
 a[6] |  2     3     -6
 a[7] |  4     0     91
 a[8] |  5     2     28

(j =  1) = (starting_pos[a[ 1].col]++) <= (starting_pos[0]++)
(j =  6) = (starting_pos[a[ 2].col]++) <= (starting_pos[3]++)
(j =  8) = (starting_pos[a[ 3].col]++) <= (starting_pos[5]++)
(j =  3) = (starting_pos[a[ 4].col]++) <= (starting_pos[1]++)
(j =  4) = (starting_pos[a[ 5].col]++) <= (starting_pos[2]++)
(j =  7) = (starting_pos[a[ 6].col]++) <= (starting_pos[3]++)
(j =  2) = (starting_pos[a[ 7].col]++) <= (starting_pos[0]++)
(j =  5) = (starting_pos[a[ 8].col]++) <= (starting_pos[2]++)
starting_pos : [3][4][6][8][8][9]

Transpose processing has been finished.

index   row   col   value
--------------------------
 b[0] |  6     6     8
 b[1] |  0     0     15
 b[2] |  0     4     91
 b[3] |  1     1     11
 b[4] |  2     1     3
 b[5] |  2     5     28
 b[6] |  3     0     22
 b[7] |  3     2     -6
 b[8] |  5     0     -15

✅ 시간복잡도

O(columns + elements)

즉, ⇒ $O(columns * row)$

참고

[자료구조 C 언어] C 프로그래밍 자료구조 - 3 (추가) : 희소 행렬