1. 관계형 데이터베이스의 구조
관계형 데이터베이스는 테이블(table)의 모임으로 구성되며, 각 테이블은 고유한 이름을 가지고 있다. 예를 들어 그림 2.1의 instructor 테이블을 보면, 이 테이블은 교수에 관한 정보를 저장하고 있다. 이 테이블은 ID, name, dept_name, salary와 같은 네 개의 열(column)을 가지고 있다. 테이블의 각 행(row)은 교수의 ID, name, dept_name, salary로 구성된 한 명의 교수에 관한 정보를 저장하고 있다.
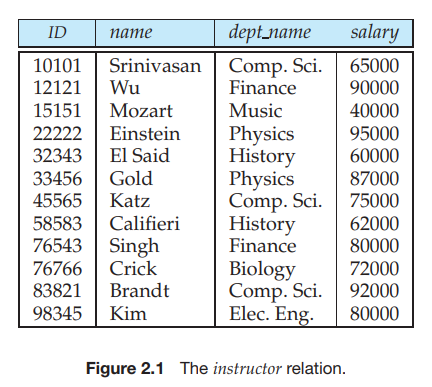
일반적으로 테이블의 각 행은 일련의 값 사이의 관계(relationship)를 표현한다. 테이블이란 이러한 관계들의 모임이므로, 테이블의 개념은 릴레이션(relation)이라는 수학적인 개념과 밀접한 관련이 있다. 이와 연관되어 관계형 데이터 모델(relational data model)의 이름도 릴레이션(relation)에 기반하고 있다. 수학적 의미의 튜플(tuple)은 간단한 값의 나열 혹은 값의 리스트를 의미한다. n개의 값에 관한 관계는 수학적으로 n-튜플로 표현된다. 즉, n개의 값을 가진 하나의 튜플이 테이블에서 하나의 행이 된다.
이처럼, 관계형 모델에서의 릴레이션(relation)은 테이블을 의미하는 단어로 사용된다. 튜플(tuple)은 테이벌의 행을 의미한다. 이와 비슷하게 속성(attribute)은 테이블의 열을 의미한다.
그림 2.1을 보면, instructor 릴레이션은 ID, name, dept_name, salary의 네 개의 속성을 가지고 있음을 알 수 있다.
우리는 앞으로 릴레이션 인스턴스(relation instance)라는 단어를 행들의 특정 집합을 포함하고 있는 릴레이션의 특정 인스턴스(instance)를 지칭할 때 사용할 것이다. 그림 2.1의 instructor의 인스턴스는 12명의 instructor를 가리키는 12개의 튜플을 가지고 있다.
릴레이션은 튜플들의 집합이기 때문에 릴레이션에서 튜플이 어떤 순서로 나타나는지는 상관없다.
릴레이션의 각 속성은 도메인(domain)이라고 하는 허가된 값의 집합을 가지고 있다. instructor 릴레이션의 salary 속성의 도메인은 가능한 모든 salary 값의 집합이고, name 속성의 도메인은 가능한 모든 교수의 이름이다.
모든 릴레이션 r에 대해서 r의 모든 속성의 도메인은 원자적(atomic)이어야 한다. 도메인이 원자적이라는 것은, 도메인의 요소가 더 이상 나누어질 수 없는 단일체라는 것을 의미한다. 예를 들어 instructor 테이블에 해당 instructor의 전화번호를 저장하는 phone_number라는 속성이 존재한다고 하면, phone_number의 도메인은 원자적이지 않을 것이다. 왜냐하면, 그 도메인의 요소는 전화번호의 집합이고, 그것은 개인 전화번호라는 부분집합을 가지고 있기 때문이다.
null값은 알려지지 않거나 존재하지 않는 값을 의미하는 특별한 값이다.
2. 데이터베이스 스키마
데이터베이스에 대해 언급할 때, 데이터베이스의 논리적 설계인 데이터베이스 스키마(database schema)와, 어떤 한 순간에 데이터베이스에 저장되어 있는 데이터의 스냅샷인 데이터베이스 인스턴스(database instance)를 잘 구별해야 한다.
릴레이션 인스턴스의 개념은 프로그래밍 언어에서 변수의 값과 비슷하다. 주어진 변수의 값은 시간에 따라 변한다. 마찬가지로, 릴레이션 인스턴스의 튜플도 릴레이션이 변경됨에 따라 변하게 된다. 하지만 일반적으로 릴레이션의 스키마는 변하지 않는다.
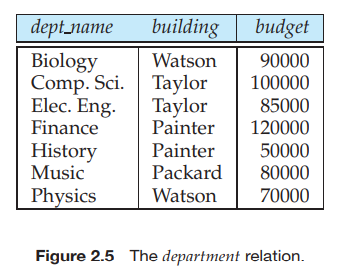
그림 2.5의 department 릴레이션의 스키마는 다음과 같다.
3. key
주어진 릴레이션 안에서 튜플을 구분하는 방법이 있어야 한다. 이것은 릴레이션의 속성(attribute)으로 표현되어야 한다. 즉, 튜플의 속성의 값은 그 튜플을 유일하게 구별할 수 있어야 한다.
3.1 superkey
superkey를 간단히 표현하면, 한 릴레이션에서 그 튜플을 유일하게 식별할 수 있도록 해주는 하나 혹은 그 이상의 속성들의 집합이다. 예를 들면, instructor 릴레이션의 ID 속성은 하나의 instructor 튜플을 다른 튜플로부터 구별하는데 충분하다. 그렇기 때문에 ID는 superkey이다.
릴레이션 r의 스키마에 존재하는 속성들의 집합을 R이라고 하자. R의 부분집합 K가 r의 superkey가 되기 위해서는, 서로 다른 튜플의 K의 모든 속성들이 같아서는 안 된다.
superkey는 관련 없는 속성을 포함할 수 있다. 예를 들면, instance 릴레이션에서 ID와 name이 superkey가 될 수 있다. 만약 K가 superkey라면 K를 포함한 어떤 집합도 superkey가 된다.
3.2 candidate key
superkey의 부분집합이 superkey가 아닌 경우가 존재할 수 있다. 그러한 최소한의 superkey를 candidate key라고 한다. 다른 여러 속성들의 집합이 하나의 candidate key 역할을 할 수도 있다. name과 dept_name의 조합이 instructor 릴레이션에서 튜플을 구분하는 데 충분하다고 하자. 그러면 {ID}와 {name, dept_name} 둘 다 candidate key이다. ID와 name 속성을 함께 사용하면 instructor 튜플을 구분할 수 있지만, ID 하나만으로도 candidate key를 이루기 때문에 {ID, name} 조합은 candidate key가 아니다.
3.3 primary key
릴레이션 안에서 튜플을 구별하기 위한 수단으로 데이터베이스 설계자에 의해 선택된 candidate key를 지칭할 때는 primary key라는 용어를 사용한다. 릴레이션의 어떠한 튜플도 동시에 key 속성에 대해 같은 값을 가질 수 없다.
3.4 foreign key
릴레이션 스키마 r1은 자신의 속성들 가운데 다른 릴레이션 스키마 r2의 primary key를 포함할 수 있다. 이러한 속성을 r1으로부터 r2를 참조하는 외래 키(foreign key)라고 한다. 릴레이션 r1은 foreign key 종속을 가진 참조하는 릴레이션(referencing relation)이라고 부르며, 릴레이션 r2는 foreign key를 가진 참조된 릴레이션(referenced relation)이라고 한다.
예를 들어, instructor 릴레이션의 dept_name 속성은 department를 참조하는 instructor로부터의 foreign key이다. dept_name은 department 릴레이션의 primary key이기 때문이다. instructor 릴레이션의 어떤 튜플 t1이 있다면, department 릴레이션에 t1의 dept_name 속성값을 자신의 primary key인 dept_name으로 가지는 튜플 t2가 존재해야 한다. 이러한 제약조건을 참조 무결성 제약조건(referential integrity constraints)이라고 한다. 이는 참조하는 릴레이션에 있는 튜플의 특정 속성에 나타나는 값은 참조되는 릴레이션의 특정 속성에 최소한 하나의 튜플이 존재해야 한다는 것이다.
4. schema diagram
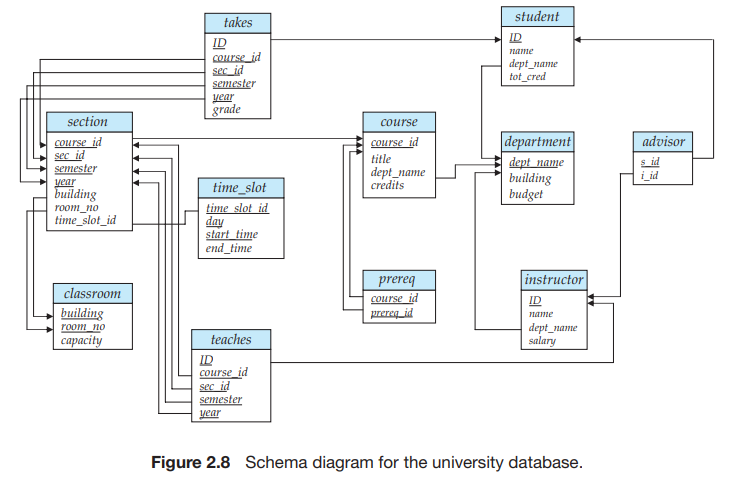
데이터베이스 스키마는 primary key와 foreign key 종속성을 가지고 있는데, 이는 스키마 다이어그램(schema diagram)을 이용하여 시각적으로 나타낼 수 있다. 그림 2.8은 대학교의 스키마 다이어그램을 나타낸다. 각 릴레이션은 네모 상자로 나타낼 수 있으며, 해당 릴레이션의 속성은 네모 상자 안에 나열되고 릴레이션의 이름은 네모 상자 위에 쓴다. primary key로 쓰이는 속성은 선을 그어서 표현한다. foreign key 종속성은 참조하는 릴레이션의 foreign key 속성으로부터 참조된 릴레이션의 primary key에 이르는 화살표로 나타낸다.
5. 관계 연산
모든 절차식 관계형 질의 언어는 하나의 릴레이션이나 릴레이션의 쌍에 적용할 수 있는 몇 가지 연산을 제공한다. 이러한 연산은 결과가 항상 하나의 릴레이션으로 표현된다는 훌륭한 속성을 가지고 있다.
조인(join) 연산은 두 릴레이션을 합치는 연산이다. 각 릴레이션에서 튜플을 하나씩 선택해서 두 튜플을 하나의 튜플로 합칠 수 있다. 릴레이션을 조인할 때 다양한 방법이 사용된다.
그림 2.12에 나타난 조인의 형태는 자연 조인(natural join)이라고 한다. instructor 릴레이션의 dept_name과 department 릴레이션의 dept_name이 같은 값을 가지는 튜플을 서로 합친 결과이다. 이와 같이 합쳐진 모든 튜플의 쌍이 결과에 나타나 있다.
카티션 곱(Cartesian product) 연산은 두 릴레이션의 튜플을 합치는데, 조인 연산과는 다르게 속성값이 일치하는지는 상관없이 두 릴레이션으로부터 가능한 모든 경우를 결과에 포함시킨다.
릴레이션은 집합이기 때문에 일반적인 집합 연산을 릴레이션에 적용시킬 수 있다. 합집합, 교집합, 차집합 등의 연산도 가능하다.
참고
Database System Concepts 6th edition 2장
