배열
배열의 성질
배열은 연속적인 메모리 공간에 순차적으로 데이터를 저장하고, 배열을 선언 할 때의 크기로 고정이 된다.
1. O(1)에 k번쨰 원소를 확인/변경 가능
2. 추가적으로 소모되는 메모리의 양(=overhead)가 거의 없음
3. Cache hit rate가 높음
4. 메모리 상에 연속한 구간을 잡아야 해서 할당에 제약이 걸림
배열의 시간복잡도
- 임의의 위치에 있는 원소를 확인/변경, O(1)
- 원소를 끝에 추가, O(1)
- 마지막 원소를 제거 O(1)
- 임의의 위치에 원소를 추가, O(N)
- 임의의 위치에 있는 원소를 제거 O(N)
하지만 파이썬에서는 배열을 대신하는 list가 사용되고 있습니다.
- 연속한 메모리에 객체(objects)의 주소를 저장한다. (파이썬의 모든 것은 객체다.)
- 같은 자료형뿐만 아니라, 다양한 자료(객체)를 저장할 수 있다.
- 배열처럼 인덱스로 각 객체(자료)에 쉽게 접근할 수 있고, 슬라이싱(slicing)할 수 있다.
리스트와 튜플의 차이점
배열에서 리스트와 비슷한 자료구조로 튜플이 있고, 이에 대한 차이점을 보겠습니다.
리스트의 특징:
- 동적 배열: 크기와 원소를 자유롭게 변경할 수 있다.
- 다양한 자료형 지원: 서로 다른 자료형의 데이터를 하나의 리스트에 저장할 수 있다.
- 인덱싱 및 슬라이싱: 배열과 유사하게, 리스트에서도 인덱싱과 슬라이싱을 통해 데이터에 접근할 수 있다.
튜플의 특징:
- 정적 배열: 한 번 생성되면 그 크기와 원소를 변경할 수 없다.
- 불변성: 튜플은 불변 객체이므로, 내용이 변경될 위험이 없는 데이터를 저장하는 데 적합하다.
연결리스트
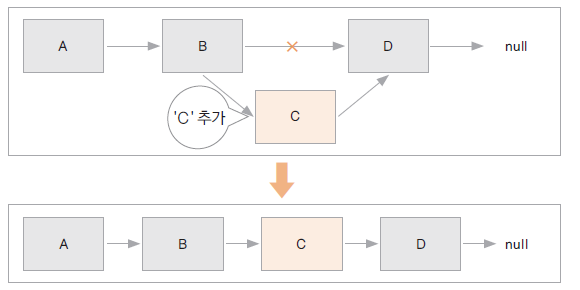
연결리스트 특징
Linked List는 인덱스를 갖지 않으며 데이터와 링크 필드를 갖고 있는 노드로 구성되어 있다. 링크에는 다음에 올 노드의 위치를 담고 있다.
링크드 리스트는 데이터를 삽입, 삭제할 경우 다음 노드의 위치를 끊고 새로운 노드의 위치를 넣으면 되므로 구조를 재정렬할 필요가 없다.
하지만 특정 데이터를 검색할 때는 Head(가장 첫 번째 노드)에서부터 순차적으로 검색해가며 자료를 찾아야 한다.
- k번째 원소를 확인/변경하기 위해서 O(k)가 필요함
- 임의의 위치에 원소를 추가/임의 위치의 원소 제거는 O(1)
- 원소들이 메모리 상에 연속해있지 않지만 Cache hit rate가 낮지만 할당이 쉽다
배열과 연결리스트 비교
| 배열 | 연결리스트 | |
|---|---|---|
| k번째 원소의 접근 | O(1) | O(K) |
| 임의 위치에 원소 접근 추가 /제거 | O(N) | O(1) |
| 메모리 상의 배치 | 연속 | 불연속 |
| 추가적으로 필요한 공간(overhead) | - | O(N) |
구간합, 누적합
구간합 또는 누적합 알고리즘은 일정 범위의 연속된 요소들의 합을 효율적으로 계산하는 데 사용됩니다. 이 방법은 주로 배열이나 리스트와 같은 연속적인 데이터 구조에서 특정 범위의 합을 빠르게 구할 때 사용됩니다. 구간합 알고리즘을 구현하는 대표적인 방법은 누적합을 미리 계산해 두는 것입니다.
누적합 알고리즘의 기본 아이디어
-
누적합 배열 생성: 주어진 배열의 각 위치에 대해, 그 위치까지의 모든 요소들의 합을 저장하는 새로운 배열을 생성합니다. 이 배열을 누적합 배열이라고 합니다.
-
구간합 계산: 특정 구간 [i, j]의 합을 구할 때, 누적합 배열을 이용하여 누적합[j] - 누적합[i-1]을 계산합니다. 여기서 i는 구간의 시작 인덱스, j는 구간의 끝 인덱스입니다.
예시
예를 들어, 배열 A = [3, 1, 4, 1, 5, 9, 2] 가 있다고 가정해봅시다. 이 배열의 누적합 배열 S는 다음과 같이 계산할 수 있습니다.
S[0] = A[0] = 3
S[1] = A[0] + A[1] = 3 + 1 = 4
S[2] = A[0] + A[1] + A[2] = 3 + 1 + 4 = 8
...
S[i] = S[i-1] + A[i]
이렇게 누적합 배열 S = [3, 4, 8, 9, 14, 23, 25]를 구한 후, 만약 구간 [2, 5]의 합을 구하고 싶다면, S[5] - S[1] = 23 - 4 = 19로 계산할 수 있습니다.
- 부분 합(Partial sum) : 처음부터 k번 인덱스까지의 합 (= A[0] + A[1] + ... A[k] )
- 구간 합(Prefix sum) : i번부터 j번 인덱스까지의 합 (= A[i] + A[i+1] ... + A[j-1] + A[j] )
코드
# 원본 배열
A = [3, 1, 4, 1, 5, 9, 2]
# 누적합 배열 계산
S = [0] * (len(A) + 1)
for i in range(1, len(S)):
S[i] = S[i-1] + A[i-1]
# 구간합 함수
def get_sum(S, i, j):
return S[j+1] - S[i]
# 구간 [2, 5]의 합 계산
print(get_sum(S, 2, 5)) # 출력: 192차원에서의 구간합, 누적합
-
2차원 누적합 배열 생성: 주어진 2차원 배열의 각 위치에 대해, 그 위치를 오른쪽 하단으로 하는 사각형 영역 내의 모든 요소들의 합을 저장하는 새로운 2차원 배열을 생성합니다. 이 배열을 2차원 누적합 배열이라고 합니다.
-
구간합 계산: 특정 구간 [x1, y1, x2, y2] (여기서 (x1, y1)은 구간의 왼쪽 상단 좌표, (x2, y2)는 오른쪽 하단 좌표)의 합을 계산할 때, 2차원 누적합 배열을 사용하여 계산합니다. 계산 방식은 다음과 같습니다:
구간합 = 누적합[x2][y2] - 누적합[x1-1][y2] - 누적합[x2][y1-1] + 누적합[x1-1][y1-1]
예시
다음과 같은 2차원 배열과 누적합 배열이 있습니다.
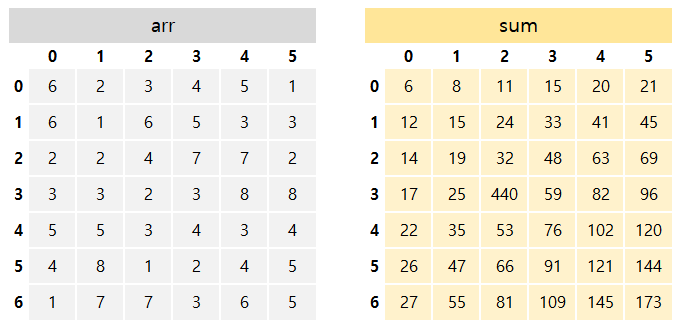
2차원 배열의 (1,2)부터 (4,4)까지의 값을 구하려면 어떻게 해야할까요?
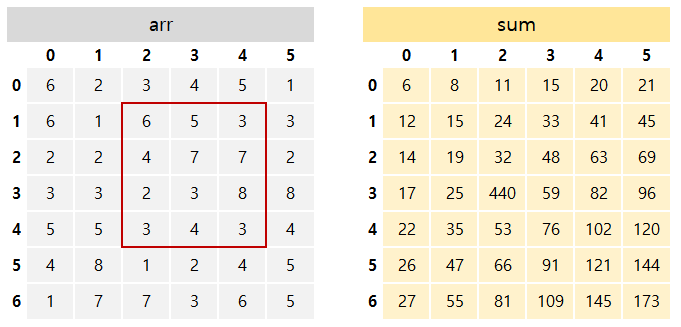
구간합 = 누적합(4,4) - 누적합(4,1) - 누적합(0,4) + 누적합(0,1)이 됩니다.