스위핑의 어려움을 알려주는 문제라고 생각한다. 2차원 평면 위의 점 75000개를 순서대로 쓸어내려가면서 각 점마다 으로 처리하는 문제다.
어떤 섬에 대해서 그 섬보다 y좌표가 작고, x좌표가 큰 섬만 방문이 가능하다. 가장 먼저 생각나는 방법은 으로 각각의 섬마다 모든 섬을 방문하여 조건에 맞는지 체크해보는 것이다. 그러나 이 방법은 의 범위와 시간 제한 때문에 적용할 수 없다.
이 문제를 해결하기 위해서는 구간 합 세그트리가 필요하다. (= 펜윅트리도 가능) 다음 그림을 보자.
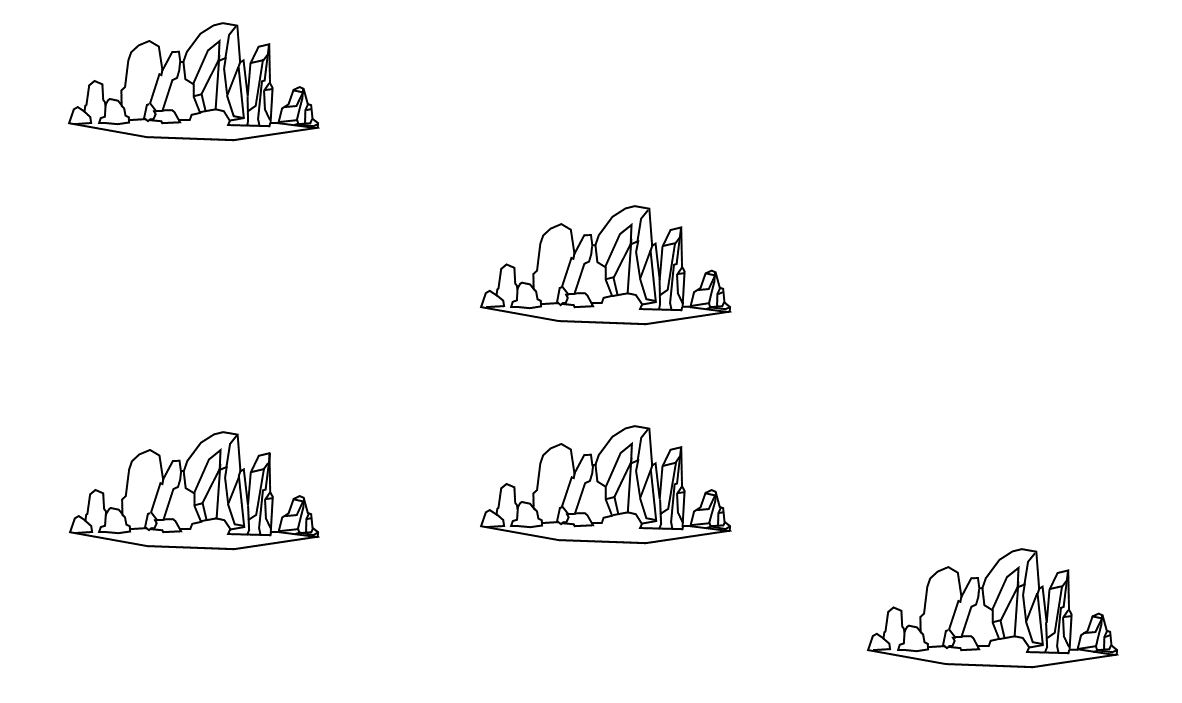
섬이 저 위치들에 5개가 놓여 있다. 각 섬에 번호를 부여해서 정렬해보자.
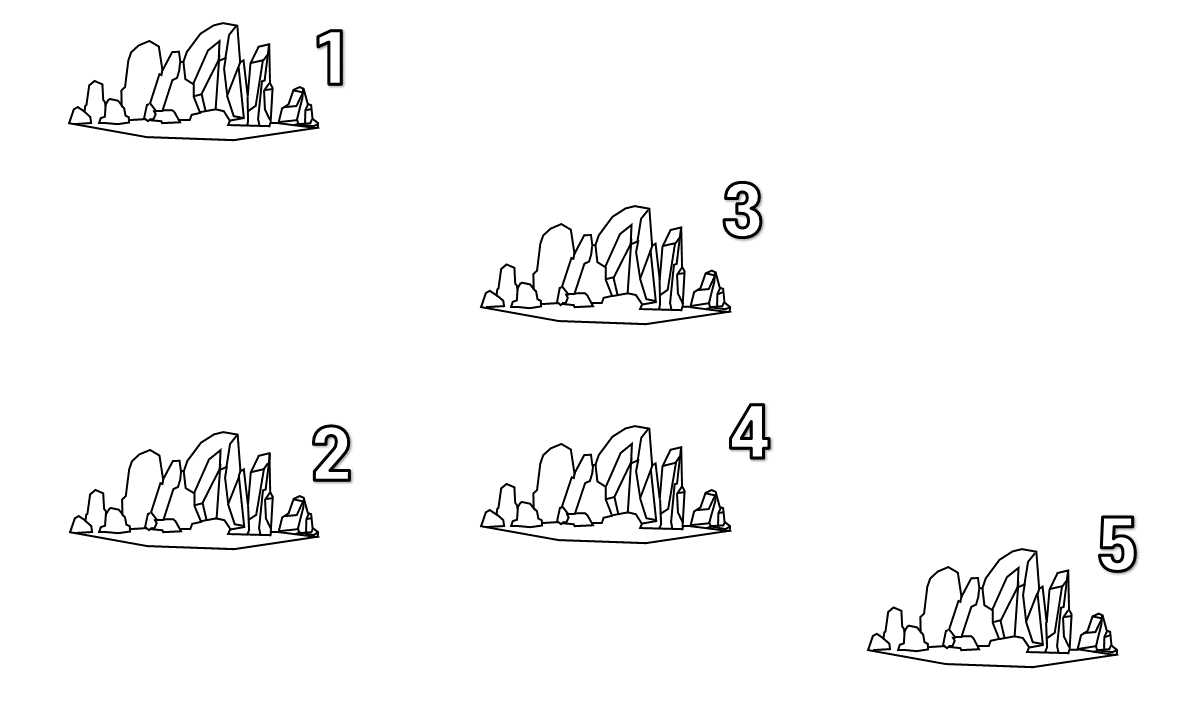
정렬 기준은 순서대로 섬을 순회할 때 i번 섬을 처리할 때면 i번 섬으로 이동할 수 있는 섬은 전부 처리된 상태가 되도록 에 대해 오름차순이고 가 같으면 에 대해 내림차순이도록 정렬한다.
여기서 가능한 의 범위가 너무 크기 때문에 적절히 좌표압축해서 1 ~ 75000까지의 범위로 만들어 놓자. (압축된 좌표만 필요하기 때문에 압축도 가능하다.)
번째 섬에 대해 번째까지의 섬은 번째 섬으로 항해할 수 있는 후보 섬들이다.
이 중에서 진짜 항해가 가능한 섬들은 좌표가 인 섬들이다.
그러므로 구간 의 합이 섬들의 개수가 되고, 구간을 구한 후에는 방금 처리한 섬을 반영하도록 업데이트 해주면 된다.
이제 1번 섬에 대해 처리를 해보자.
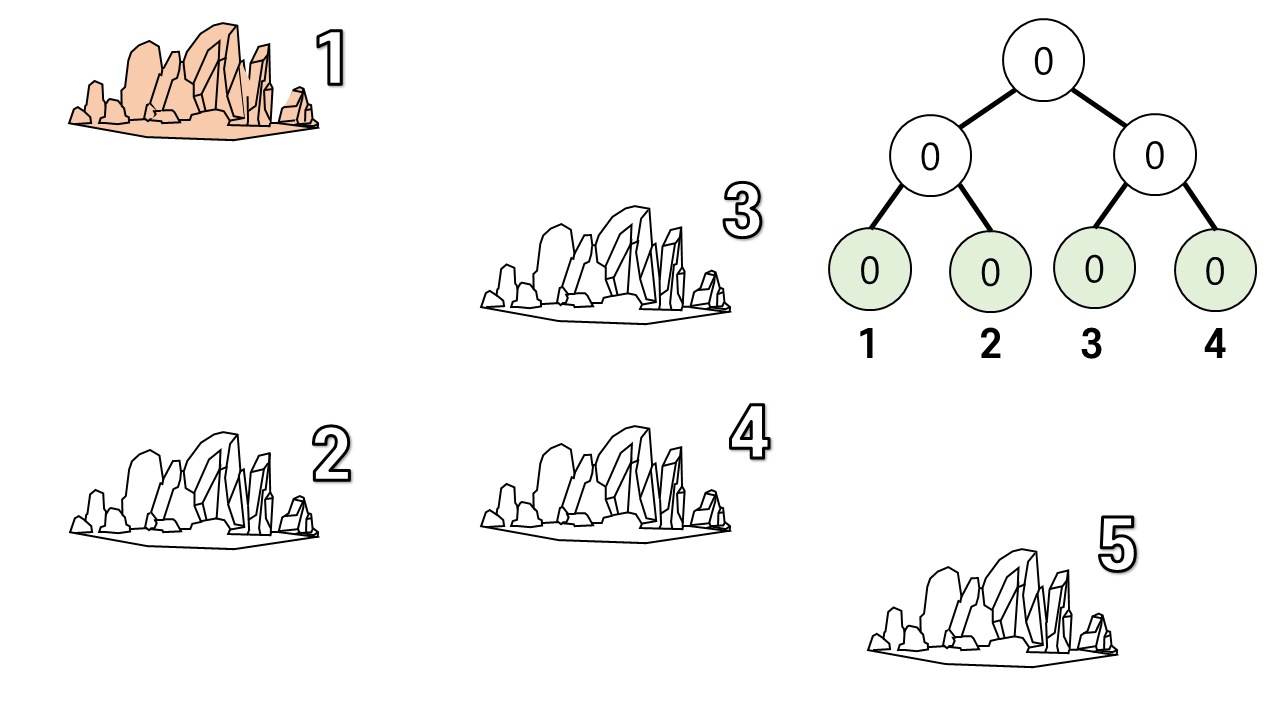
1번 섬은 이므로 구간 의 구간합인 0개의 섬이 1번 섬으로 항해할 수 있다.
이후 세그트리에 인 섬 1개를 추가하자.
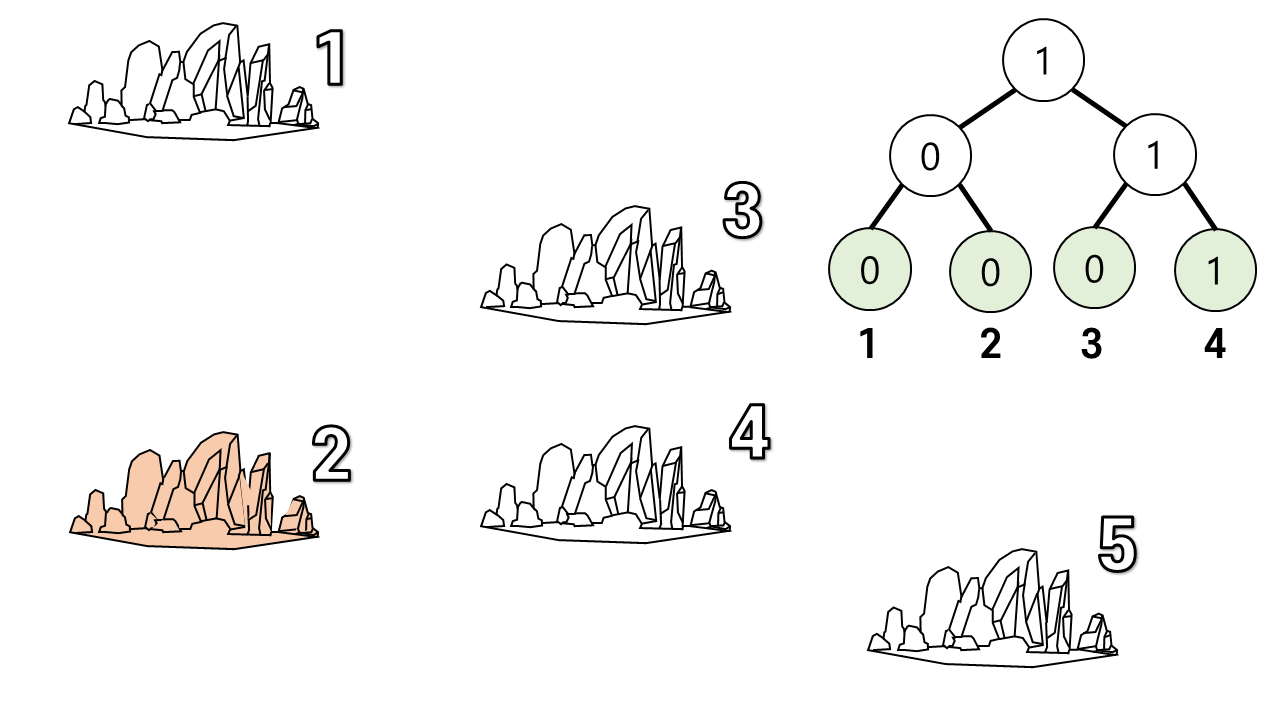
이제 2번 섬을 보자.
2번 섬은 이므로 2번 섬으로 항해할 수 있는 모든 섬은 에 등록되어 있다.
구간합은 1이므로 1개의 섬이 2번 섬으로 항해할 수 있다.
이후 세그트리에 인 섬 1개를 추가하자.
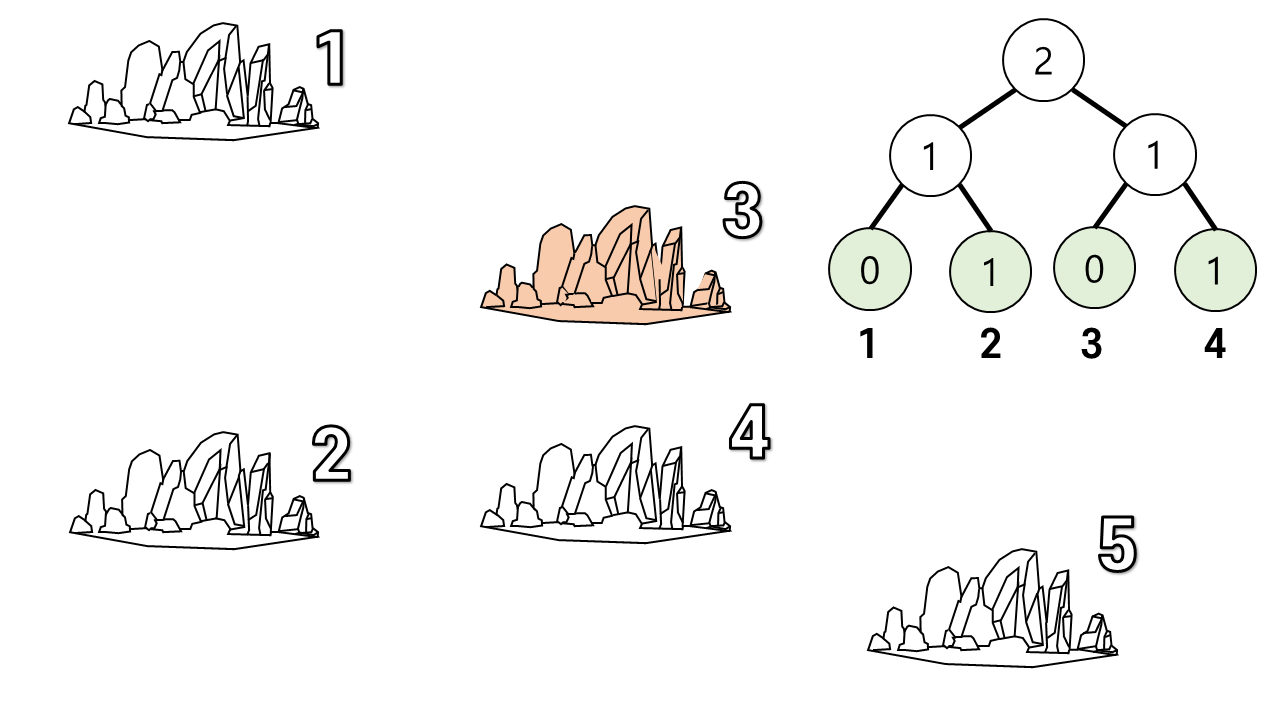
3번 섬은 이므로 구간합 인 1이 3번 섬으로 항해해서 올 수 있는 섬의 개수이다.
이후 세그트리에 인 섬 1개를 추가하자.
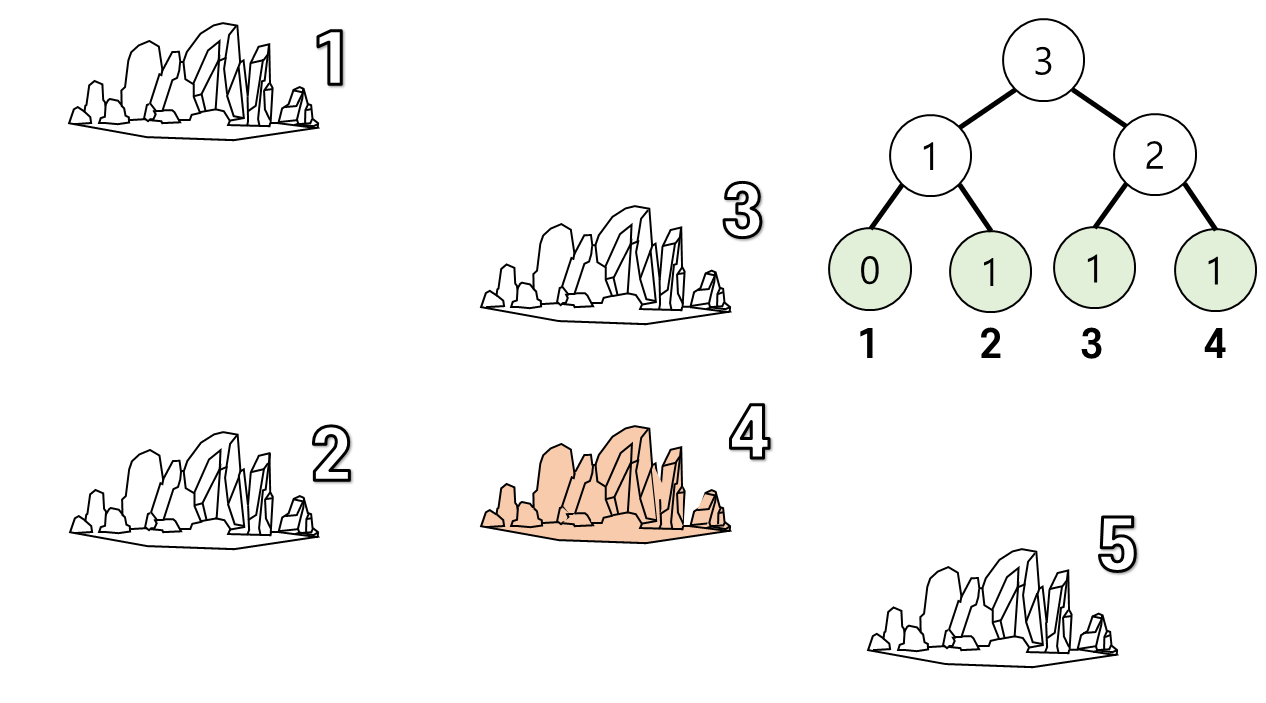
구간합 는 3이므로 4번 섬으로 올 수 있는 섬은 3개다.
이후 세그트리에 인 섬 1개를 추가하자.
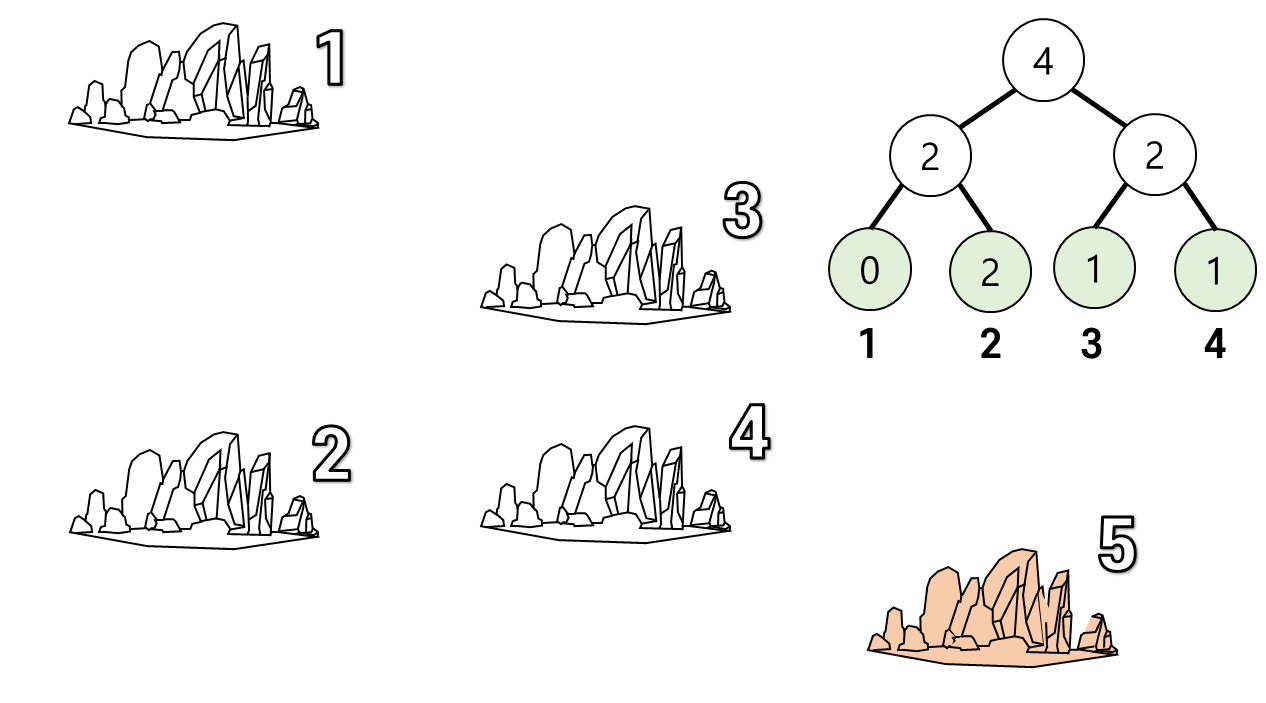
마지막 섬은 이므로 구간합 인 4가 5번 섬으로 올 수 있는 섬의 개수이다.
따라서 모든 항해 가능한 섬의 쌍은 0+1+1+3+4 = 9 개가 된다.
세그트리는 요즘 문제를 새로 풀 때마다 다시 구현하는 연습을 하고 있다. 완전히 숙달될 때까지 아마 계속 구현 연습을 할 듯 하다.
코드
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif
#define FASTIO ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define ll long long
#define debug if constexpr (local) std::cout
#define endl '\n'
class SegTree{
private:
vector<ll> tree;
public:
SegTree(int N){
tree.resize(4*N);
}
ll init(vector<ll> &nums, ll node, int s, int e){
if (s == e) return tree[node] = nums[s];
return tree[node] = init(nums, node*2, s, (s+e)/2) + init(nums, node*2+1, (s+e)/2+1, e);
}
ll update(ll node, int s, int e, int idx, int add){
if (idx < s || e < idx) return tree[node];
if (s == e) return tree[node] += add;
return tree[node] = update(node*2,s,(s+e)/2,idx,add)+update(node*2+1,(s+e)/2+1,e,idx,add);
}
ll query(ll node, int s, int e, int l, int r){
if (e < l || r < s) return 0;
if (l <= s && e <= r) return tree[node];
return query(node*2,s,(s+e)/2,l,r) + query(node*2+1,(s+e)/2+1,e,l,r);
}
};
struct Dot{
int x, y;
};
bool cmp(Dot a, Dot b){
if (a.x != b.x) return a.x < b.x;
return a.y > b.y;
}
bool cmpY(Dot a, Dot b){
return a.y < b.y;
}
vector<Dot> Island;
vector<ll> yarr;
void solve(){
int N; cin >> N;
vector<Dot> Island;
vector<ll> yarr;
SegTree SG(75005);
for (int i = 0; i < N; i++){
int x, y; cin >> x >> y;
Island.push_back({x, y});
yarr.push_back(y);
}
//compress
sort(Island.begin(), Island.end(), cmpY);
ll cy = 0, prev = -2147483648;
for (auto &i: Island){
if (prev < i.y){
cy++;
}
prev = i.y;
i.y = cy;
}
sort(Island.begin(), Island.end(), cmp);
ll mxv = cy;
ll sum = 0;
for (auto &i: Island){
sum += SG.query(1, 1, mxv, i.y, mxv);
SG.update(1, 1, mxv, i.y, 1);
}
cout << sum << endl;
/*for (auto &i: Island){
debug << "(" << i.x << ", " << i.y << ")\n";
}*/
}
int main(){
FASTIO;
int T; cin >> T;
while (T--){
solve();
}
}