BOJ 기록
1.BOJ 2343 | 기타 레슨
처음에는 녹화되는 강의는 연속적이어야 한다는 조건을 못 보고 그리디하게 풀면 안 되는 문제인 줄 알았다...
2.BOJ 6236 | 용돈 관리
간단한 Parametric Search 문제
3.BOJ 3079 | 입국심사
항상 문제 범위를 잘 읽어봐야겠다...T_k \* max(M)인 1e18이 초기 hi 값이어야 한다.그러므로 int가 아닌 long long int 로 변수를 선언해야 오버플로우가 나지 않는다.
4.BOJ 2357 | 최솟값과 최댓값

수업 때 핸드폰으로 풀다가 어딘가 상당히 어긋난 채로 오류투성이 코드를 만들었던 문제...
5.BOJ 2912 | 백설공주와 난쟁이
어렵다. Sqrt Decomposition으로 풀려고 했는데 내 머리로는 이 이상 최적화가 안 된다.
6.BOJ 13547 | 수열과 쿼리 5
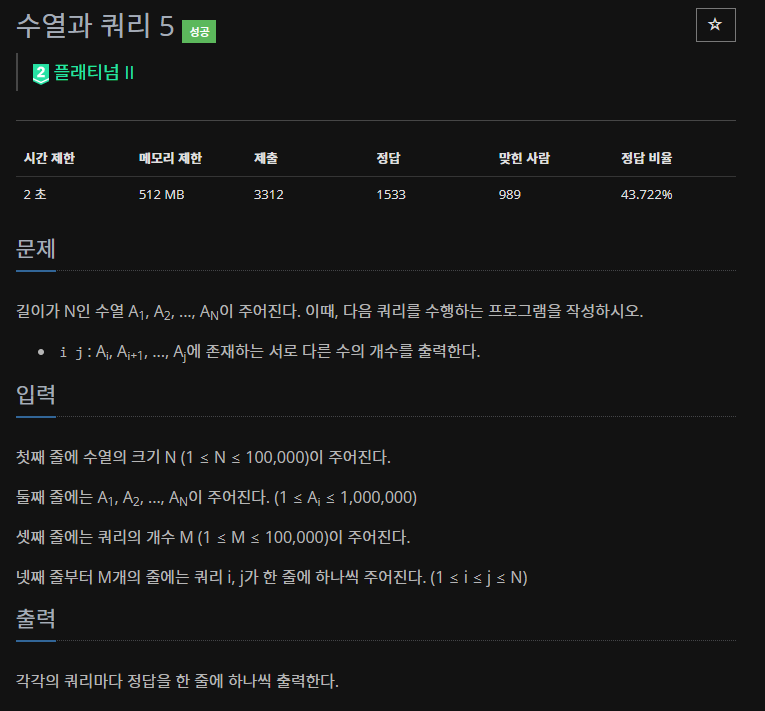
mo's 알고리즘으로 쿼리를 정렬해 푸는 문제이다. 바로 전에 평방 분할로 문제를 풀려고 엄청나게 난리치다가 mo's 배우고 이런거 푸니까 심신이 안정된다.
7.BOJ 13548 | 수열과 쿼리 6
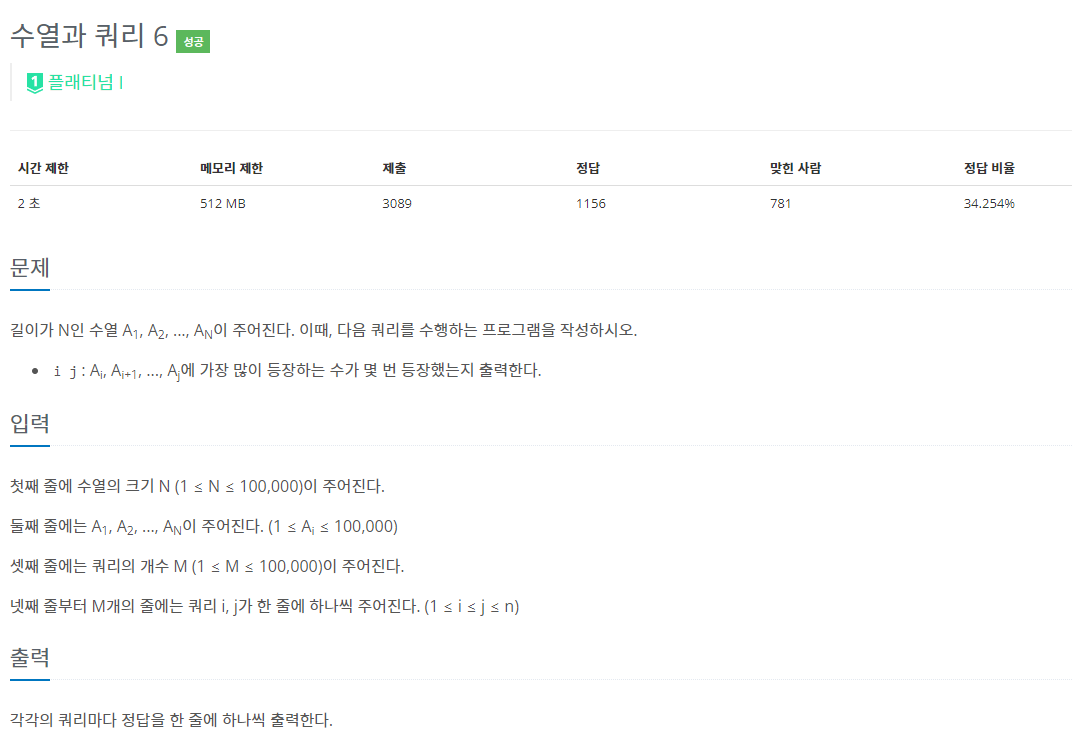
mo's 알고리즘을 이용해서 푸는 어려운 문제이다.
8.BOJ 8462 | 배열의 힘
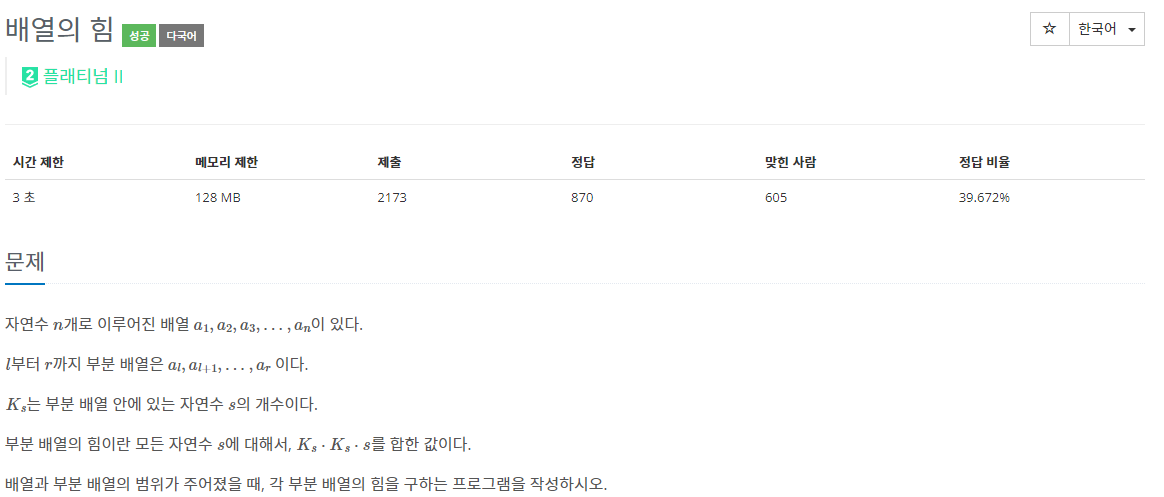
l, r 범위 내의 부분 배열에서의 모든 자연수 s에 대해 K_s를 그 부분 배열 내의 s의 개수라고 하고, 모든 s의 (K_s)^2 \* s 를 구하는 문제다.(n+1)^2 - n^2 = 2n+1 이라는 간단한 원리로 해결했다.역시나 mo's 알고리즘 연습 문제다.
9.BOJ 18185, 18186 | 라면 사기

BOJ 18185 라면 사기 (Small)BOJ 18186 라면 사기 (Large)HI-ARC 디코방에서 누가 하루종일 푸셨다고 해서 찾아보게 되었다.처음 볼 때 그리디인가? 싶었고 알고리즘 분류 보고 확신했다.사실 DP인가 그리디인가 헷갈려서 좀 고민하긴 했다.라면
10.BOJ 13546 | 수열과 쿼리 4
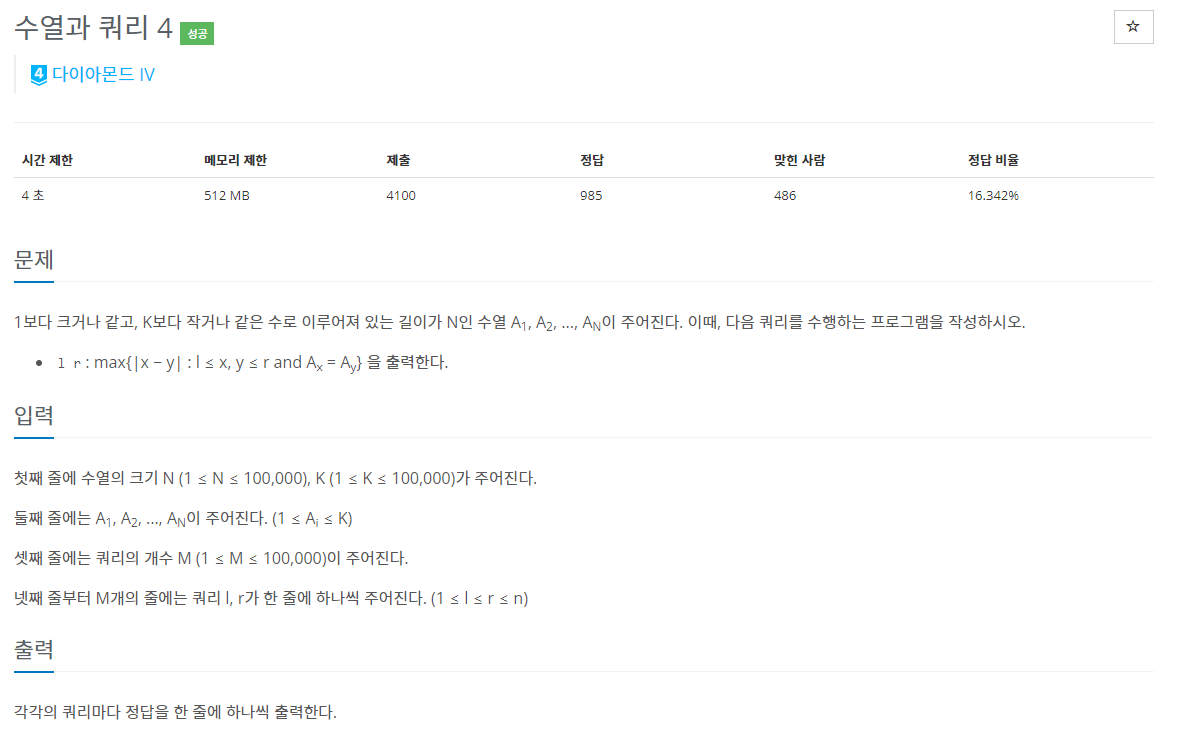
아이디어는 고민해보니 떠오르는데 어디선가 자꾸 틀려서 나를 미치게 했던 문제다.뭔가 오류는 발견되고 수정되는데 계속 1%컷나는게 정신에 심대한 악영향을 주었다;;마지막에 MaxDistance를 연산하는 부분에서 SIZE_PER_BUCKET을 BUCKET_SIZE로 잘못
11.BOJ 13545 | 수열과 쿼리 0
수열과 쿼리 4를 풀었다면 날먹이 가능하다는 글을 읽고 도전해 보았다.우선, i~j의 합은 계산해 놓은 누적합 배열이 psum이라고 할 때 psumj - psumi-1이다.이 합이 0이려면 psumi-1 = psumj 이면 되는 것이다.따라서 같은 값의 최대 거리를 찾
12.BOJ 13550 | 수열과 쿼리 7
수열과 쿼리 0과 완전히 같은 문제이다.다만 수열과 쿼리 0은 마이너스 값까지 신경써야 했다면 이 문제는 그런 게 없는 대신 (psumj - psumi-1) % K == 0을 찾는 것이므로 모든 psum 값에 mod K 를 해 주어야 한다.2 <= K <=
13.BOJ 13704 | 수열과 쿼리 11
수열과 쿼리 0에서 쓰인 prefix sum과 비슷한 기법을 사용한 문제이다.prefix xor 정도로 부를 수 있겠다.XOR 연산의 성질인 교환법칙과 결합법칙이 성립한다 정도만 생각해도 풀 수 있겠다.$Ai$ ^ $A{i+1}$ ^ ... ^ $A\_{j}=K$ 인
14.BOJ 11399 | ATM

23238번 풀다가 도저히 생각이 안 나서 뇌풀기 겸으로 잠시 힐링했습니다.i번 사람이 돈을 인출하는 데 필요한 시간은 $P_1+P_2+...+P_i$ 입니다.그러므로 N번 사람까지 모두 인출하려면 $N×P_1 + (N-1)×P_2 + ... + P_N$ 이므로 작은
15.BOJ 11047 | 동전 0
마음 편하게 짜면 되는 그리디 문제다.오답이 나올 여지가 없는 문제라서 정말 힐링이 된다.금액이 큰 단위의 동전부터 최대한 사용하면 되기 때문에 입력받은 순서 반대로 그리디를 돌리면 된다.
16.BOJ 23238 | Best Student
2일간 많은 실패와 고민을 하며 풀어낸 문제다.처음에는 수열과 쿼리 6의 코드를 기반으로 작성했는데, $O(Q\\sqrt{N})$ 복잡도의 코드에 각 Add 와 Remove 함수 실행시마다 set에 값을 저장하고 검사하도록 하여 $O(Q\\sqrt{N} logN)$이라
17.BOJ 6515 | Frequent values
수열과 쿼리 6과 푸는 방법이 같습니다.범위에 신경써서 $a_n$을 전부 양수로 만들어 줄 수 있도록 합니다.저는 Best Student를 푼 직후였기 때문에 좌표압축을 그대로 이용했습니다.
18.BOJ 17731 | Historical Research
일본어는 할 줄 모르지만 구글 번역기의 힘을 빌려 읽어냈다.큰 틀은 이 문제는 시간제한이 4초라 넉넉하기 때문에 마치 제곱근 분할이 정해인 것처럼 느껴진다.코드
19.BOJ 1987 | 알파벳
Class 5 문제들 순회하면서 내실을 다지려고 처음으로 고른 문제다.고등학생 때 쿼리를 이해 못해서 못 풀었던 게 한이었는지 갑자기 쿼리에 꽂혀서 그것만 풀었던지라 DFS 문제는 오히려 생소하다.그래도 확실히 요즘 머리 싸매고 문제 풀면서 고민하는 게 감각을 많이 되
20.BOJ 1717 | 집합의 표현
간단한 Union Find 구현 문제다.Union Find 알고리즘은 Disjoint set 을 나타내는 알고리즘인데, 간단히 말하면 겹치는 부분이 없는 집합을 말한다.${1, 2}, {3}, {4}$ 처럼 부분집합들 사이에 겹치는 부분이 없는 것을 서로소 집합이라고
21.BOJ 1197 | 최소 스패닝 트리
최소 스패닝 트리를 구현하라는 아주 간단한 문제다.나는 크루스칼 알고리즘으로 구현했는데 이게 아주 편해서 프림 알고리즘은 생각도 안 날 정도다 ㅋㅋㅋㅋUnion Find 클래스를 만들어 놓으니까 문제 풀기에 아주 좋다.아직 최소 스패닝 트리의 응용 문제를 안 봤는데 어
22.BOJ 2252 | 줄 세우기
처음 봤을 때는 그리디인가? 싶어서 몇 가지 따져봤는데 (l, r)에서 r이 움직여야 하는지 l이 움직여야 하는지 판단할 수 없는 때가 생겼다.그래서 그래프 문제라고 생각했고 위상 정렬을 구현해서 맞았다.코드
23.BOJ 13459, 13460, 15644 | 구슬 탈출 1, 2, 3
읽어보면 알겠지만 그냥 구현이다. BFS인가 DFS인가 긴가민가했지만 깊이가 10밖에 안 되는 것을 보니 DFS 때리면 맞겠다 싶었다. 다들 구현이 어렵다고는 하는데 아마 공 2개가 충돌하는 경우 때문이 아닌가 싶다. 그래서
24.BOJ 12100 | 2048 (Easy)
음... 4방향 전부 각기 다른 함수로 구현해야 해서 조금 짜증나는 구현이었다.실수했던 부분은 한 움직임에서는 merge된 블럭이 다시 merge할 수 없다는 점을 간과한 것이다.그것 말고는 dfs 써서 그냥 구현해주면 된다.코드
25.BOJ 12094 | 2048 (Hard)
솔직히 당황했다. 어디서 최적화를 해야 할 지 처음에 감이 안 잡혀서 고생했는데, 질문 게시판을 좀 보고 깨달았다.Move 후 변화가 없다면 이후 탐색은 무의미하다.maxvalue를 업데이트하면서 현재 깊이에서 도달 가능한 범위인지 체크한다.2번이 핵심인데, 이 문제는
26.BOJ 20040 | 사이클 게임
Union Find 기본 문제이다.처음에는 노드를 연결할 때마다 사이클이 있는지 탐색하려고 했지만 N과 M의 범위를 보니 시간초과가 날 것 같아서 다른 방법을 고민했다.그러다가 최소 스패닝 트리를 구현할 때 Union Find를 써서 Cycle이 형성되는지 체크했던 기
27.BOJ 23325 | 마법천자문
정석적인 DP 문제다.요즘 DP를 거의 안해서 DP력이 크게 떨어졌다는 사실이 확 느껴지는 문제였다.역시 수능 + 겨울방학 조합은 사람을 엄청 무디게 만드는 것 같다. <수> <연산자> <수> <연산자> 같이 번갈아 나오는 특성을 이용해서 초기값은
28.BOJ 10942 | 팰린드롬?

처음에 떠올린 아이디어는 $s, e$ 구간이 들어오면 실시간으로 $s, e$ 구간이 팰린드롬이 맞는지 검사해서 출력하는 것이다.$N=2000$ 정도면 재귀함수로도 무리 없이 돌아갈 거라고 생각해서 구현했더니 무난하게 AC 나왔다.사실 $O(N^2)$으로 전처리 해서 쿼
29.BOJ 1005 | ACM Craft

뉴비절단기로 악명높은 ACM Craft이다. solved.ac가 활성화된 지금은 문제의 난이도를 티어로 볼 수 있고. Class로 분류되어 있는 좋은 문제들이 많아 뉴비가 멋모르고 이 문제에 접근할 일은 많지 않다.그러나 solved.ac이 없었던 시절에는 백준을 10
30.BOJ 9251 | LCS
고등학생 때 공부했던 건 다 잊어먹은건지 분명 아는건데 어떻게 푸는지 기억이 나지 않았던 문제다. 아! LCS! 아시는구나! 근데 어캐 푸는거였지?우선 $LCS$는 Longest Common Subsequence의 약자로 가장 긴 공통 부분 수열을 찾는 것이다.착각하면
31.BOJ 1958 | LCS 3
처음에는 LCS 연산을 2회 해서 해결하려고 했으나 그렇게 만만한 문제는 아니었다.생각해보면 LCS 연산은 해가 유일한 연산이 아니라서 길이가 같은 다른 해가 나올 수도 있고, 연산하는 방법에 따라서 다른 답이 나올 수 있어서 이렇게는 해결이 불가능하다.그래서 문자열
32.BOJ 2565 | 전깃줄

LIS 문제라는 것을 알고 풀었기 때문에 아이디어는 한 번에 보였고, 두 가지 방법으로 구현해서 풀었다.첫 번째는 $O(N^2)$으로 구현했는데, 다음과 같은 코드로 작성했다.원리는 간단하다.$dpi$는 $arri$까지의 LIS 길이를 담게 하고, $dpi+1$을 구하
33.BOJ 13711 | LCS 4
진짜 전형적인 구현 쉽고 아이디어 어려운 문제다.근데 사실 LCS를 특정한 조건 아래서 $O(NlogN)$으로 푸는건 너무 웰노운이라서 이게 P5를 줘도 되나 싶긴 한데그걸 모르고 풀면 P5 이상을 줘도 될 것 같다.사실 LCS 좀 연습하려고 LCS 번호순으로 순회하다
34.BOJ 18438 | LCS 5
LCS 1부터 풀다가 결국 여기까지 왔는데 난이도가 갑자기 미친듯이 수직상승하는게 백준 1000번부터 번호순으로 푸는 느낌이라서 재밌다. 과연 LCS 6은 얼마나 어려울까?일단 메모리 제한이 4MB인 것부터 극한의 최적화를 요구하는 문제임을 짐작할 수 있다.int형 변
35.BOJ 18440 | LCS 7
LCS 6을 풀었다면 LCS 5와 조합해서 풀 수 있다. 나는 이걸 LCS 6을 풀고도 시간 초과때문에 한참을 더 풀었지만 기본적인 아이디어는 LCS 6과 같으므로 LCS 6은 생략한다.우선 LCS는 최장 공통 부분 수열이다. 보통은 $O(NM)$으로 구할 수 있지만
36.BOJ 17161 | 편집 거리 (Hard)
LCS 5를 풀었기 때문에 16MB라는 메모리 제한에서 익숙한 히르쉬버그의 향기가 느껴지는 문제였다.히르쉬버그를 이미 공부했기 때문에 이 문제는 처음부터 구현할 방법이 바로 떠올랐다.사소한 실수 한 번 이후에 바로 AC를 맞은 의외로 쉬웠던 문제였다.이 문제 유형은 간
37.BOJ 2473 | 세 용액
간단한 이분탐색 문제인데 한참 헤맸다.난 정렬한 수열에서 양 끝 점을 잡고 투 포인터로 점점 좁혀나가면서 그리디를 수행했는데, 계속 WA가 나와서 아이디어에 문제가 있다는 걸 알았다.뭔가 어떤 case에서 정답을 놓치는 일이 발생하는 것 같은데, 그게 어딘지 모르겠어서
38.BOJ 1708 | 볼록 껍질

Convex Hull 알고리즘의 입문 문제다. 볼록 껍질은 주어진 점으로 구성되었지만 점들을 모두 감싸는 다각형을 말한다. 알고리즘 구현 자체는 쉽지만 응용 문제들이 이상한 거하고 같이 섞여 나와서 좀 두렵다. Convex Hull 알고리즘의 입문 문제다. 볼록 껍
39.BOJ 10254 | 고속도로
요구하는 조건은 아주 간단하지만 구현이 생각보다 어려운 문제다.2차원 평면 위에 놓여진 도시들 중 가장 먼 도시를 찾아라. 즉 N개의 점을 전부 비교해서 $O(N^2)$에 해결하는 솔루션이 제일 먼저 떠오른다.그러나 도시의 개수가 최대 200,000이므로 절대 $O(N
40.BOJ 7420 | 맹독 방벽
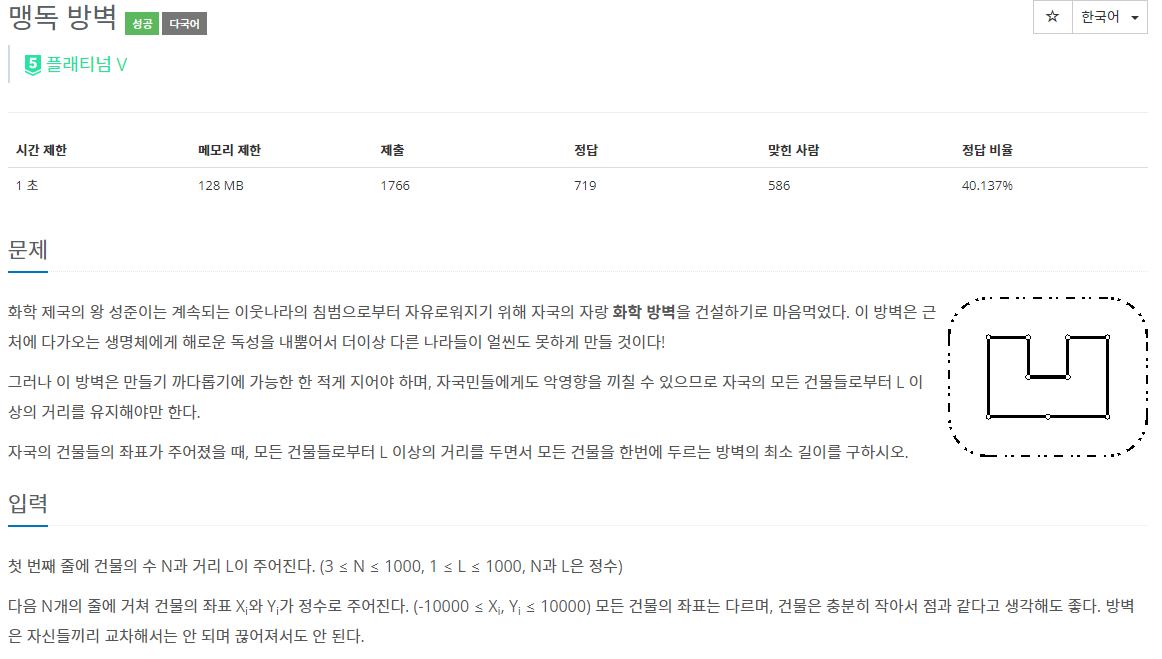
문제를 처음 보고 처음에 직관적으로 아 이거 그냥 볼록 껍질 구하고 원 하나 더하면 되는거 아닌가 생각을 했었는데 정작 문제를 읽다가 오히려 이해가 더 안돼서 좀 돌아갔던 문제였다.볼록 껍질의 둘레를 구해서 반지름이 L인 원의 둘레와 더해주면 된다.왜 그런가는 사실 너
41.BOJ 3679 | 단순 다각형
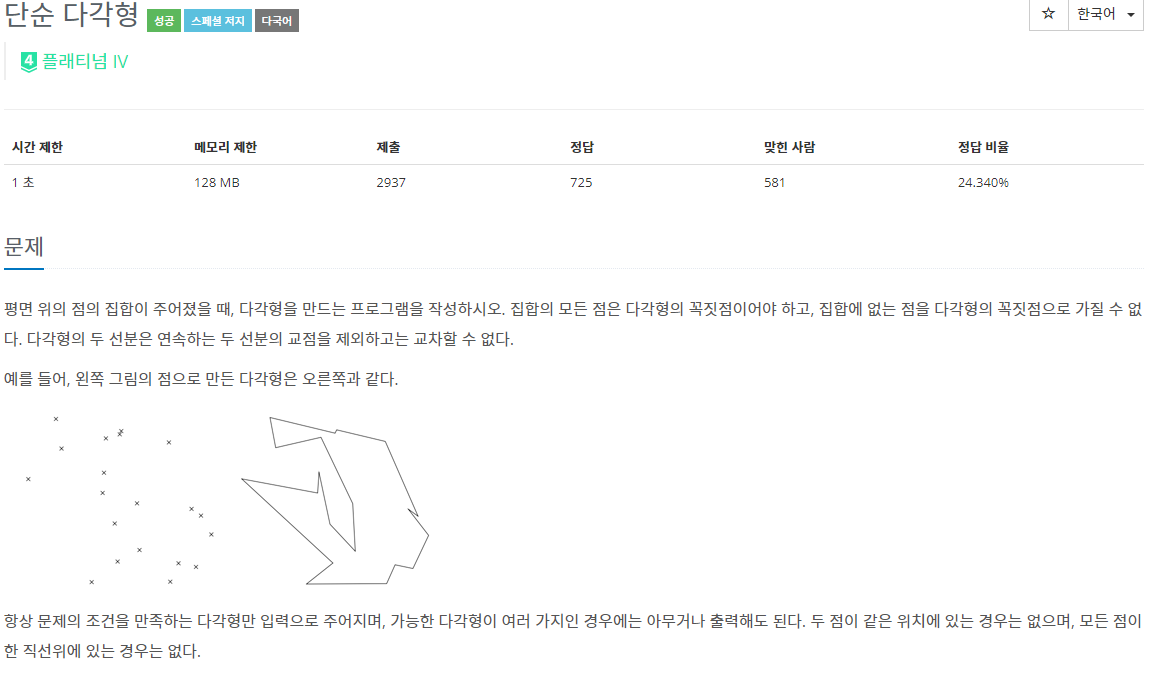
Convex Hull을 구할 필요는 없고, 전처리 과정이었던 그라함 정렬만 해주면 된다.다만 나도 몇번 틀렸던 부분이 있는데, 정렬 과정에서 시작과 끝 몇개의 점이 직선상에 놓인 경우를 생각해보자.이런 상황에서 거리를 기준으로 가까이 있는 것부터 계산하도록 정렬하는게
42.BOJ 4225 | 쓰레기 슈트
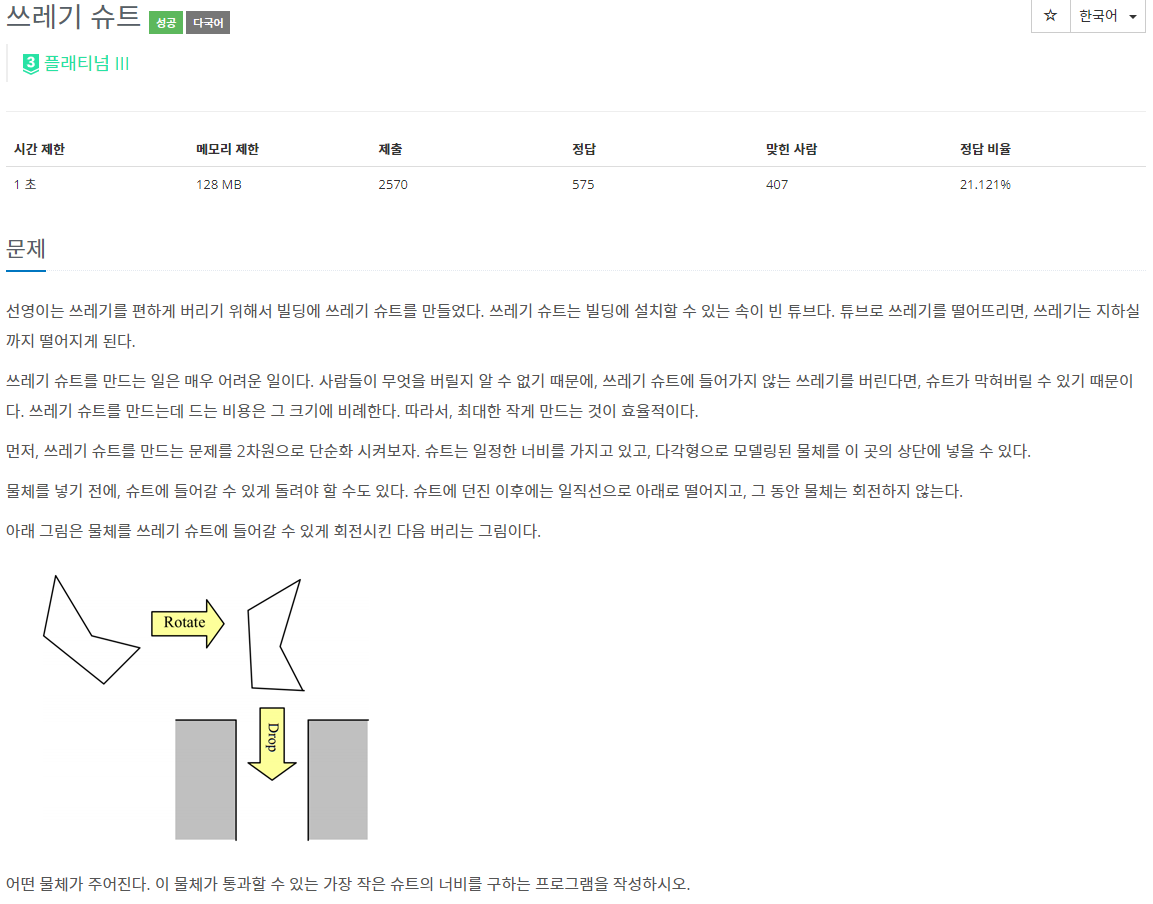
이 문제는 Convex Hull 없이도 풀리는 문제다.N이 최대 100이기 때문에 모든 점에 대해 검사하는 $O(N^3)$으로 충분히 풀린다.그러나 N을 조금 늘리기만 해도 이 방법은 통하지 않으므로 볼록 껍질을 구해서 $O(N^2)$으로 해결하는 방법이 더 나을 것이
43.BOJ 9240 | 로버트 후드
딱 봐도 고속도로(https://velog.io/@bformat/BOJ-10254-%EA%B3%A0%EC%86%8D%EB%8F%84%EB%A1%9C이렇게 날로 먹을 수 있는 문제들이 너무 많다.고속도로(코드
44.BOJ 4181 | Convex Hull
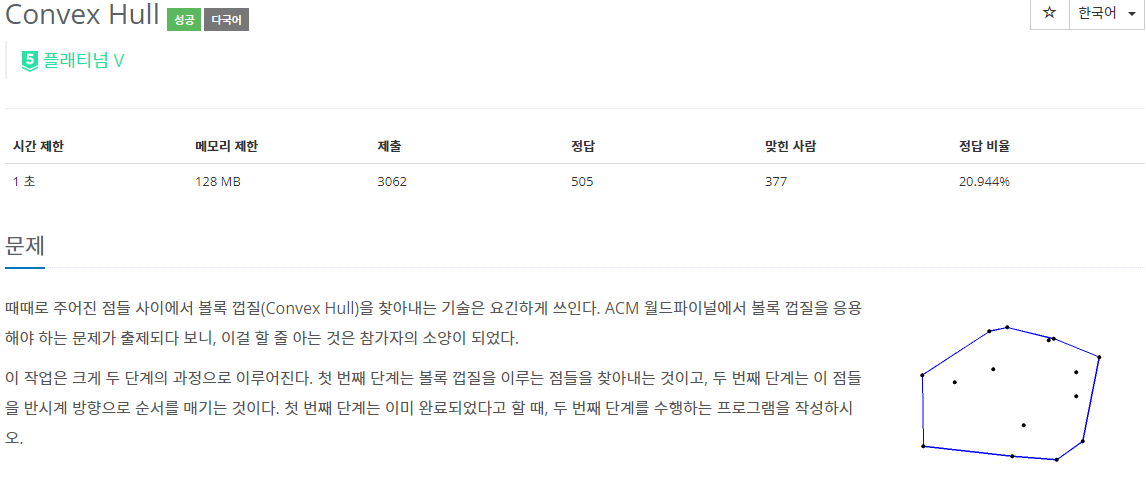
컨벡스 헐이 제목인데 컨벡스 헐이 필요 없는 문제가 있다?놀랍게도 이 문제를 푸는데 컨벡스 헐 알고리즘은 필요가 없다. 우리는 주어지는 점들을 정렬만 해주고 \*\*단순 다각형(코드
45.BOJ 15028 | Breaking Biscuits
= 쓰레기 슈트 (https://velog.io/@bformat/BOJ-4225-%EC%93%B0%EB%A0%88%EA%B8%B0-%EC%8A%88%ED%8A%B8코드
46.BOJ 15420 | Blowing Candles
\*\*쓰레기 슈트(그러므로 회전하는 캘리퍼스를 이용해서 모든 직선에 대한 가장 먼 점의 거리를 구해서 $O(N)$에 해결해야 한다.개인적으로는 이 문제의 티어가 #4225나 #15028과는 다르게 더 높게 책정되어야 한다고 생각한다. 이 문제만 회전하는 캘리퍼스까지
47.BOJ 15311 | 약 팔기
이 문제를 처음 보자마자 이진수가 떠올랐다. 1 2 4 8 ... 등의 수가 있다면 다음 자릿수 - 1까지의 모든 수를 만들 수 있기 때문이다.그러나 이 문제는 그렇게 풀 수 없다. 알약이 연속된 자리에 위치해 있어야 하기 때문이다.여기서 이 문제를 만든 사람의 굉장히
48.BOJ 13310 | 먼 별

Convex Hull, Rotating Callipers에 대해 완전히 이해하고 있는 상태로 시도해야 풀 가능성이 보이는 문제다.만약 삼분 탐색이 쓰인다는 것을 알고 있다면 이 문제는 단순한 구현 문제가 되겠지만, 실제로 이 문제를 보자마자 삼분탐색이라고 바로 알아채기
49.BOJ 2389 | 세상의 중심에서...
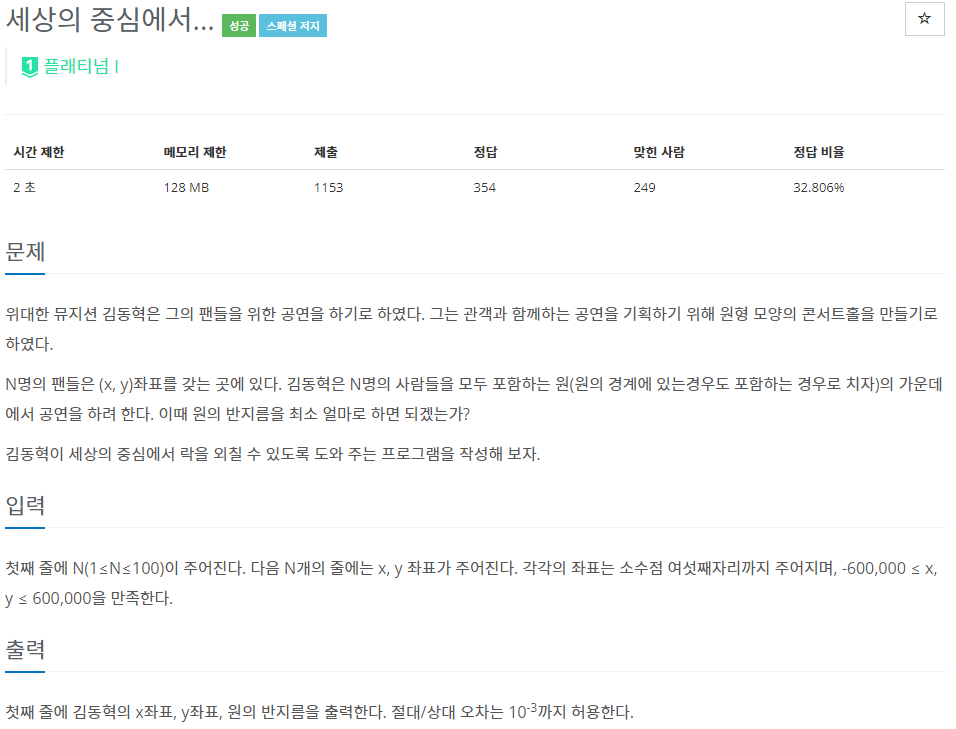
사실 이건 ㄹㅇ 날먹 문제가 맞다.최소 외접원 계열 문제는 죄다 경사하강법으로 해결이 가능하다.최소 외접원을 구하기 위해 휴리스틱으로 계속 지워나가면서 푸는 $O(N)$ 알고리즘의 존재는 알고 있다.근데 내가 그걸 쓸 줄 모르기도 하고, 애초에 최소 외접원 계열 문제는
50.BOJ 21182 | Weird Flecks, But OK
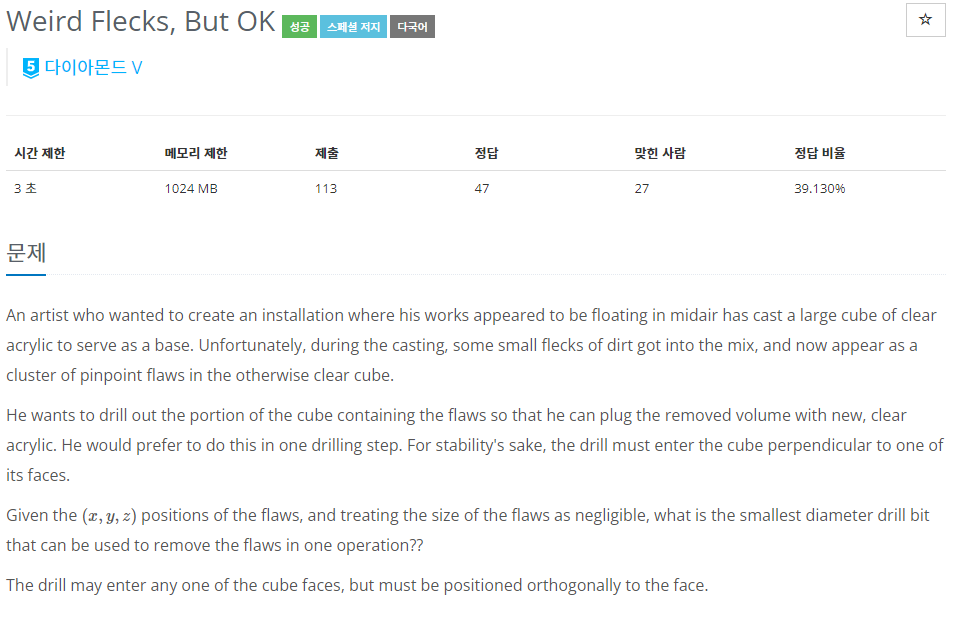
문제를 처음 보면 조금 당황할 수 있는데 'The drill may enter any one of the cube faces, but must be positioned orthogonally to the face. ' 문장만 없다면 문제가 좀 어려워지기 때문이다.그래서
51.BOJ 11930 | Smallest Enclosing Sphere
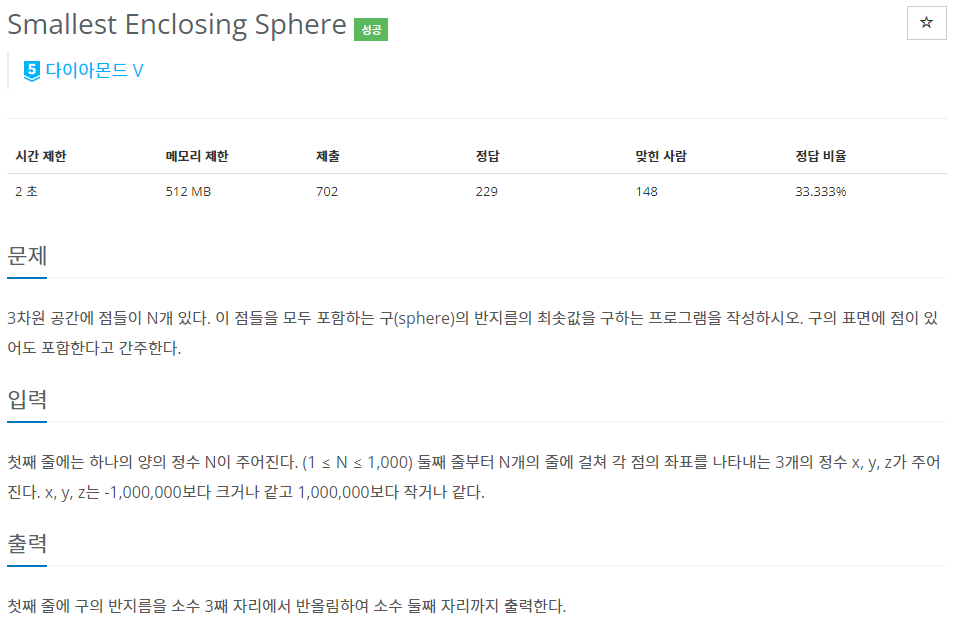
$f(x, y)$에 대해 최소 외접원을 구하는 방법은 \*\*세상의 중심에서(동일한 방법으로 $f(x, y, z)$에 대한 최소 외접구를 구할 수 있다. 그러니까 그냥 똑같은 문제라고 생각하면 된다.코드
52.BOJ 25433 | PLCS

이걸 처음에 역추적까지 해야 한다고 생각해서 메모리 초과를 좀 많이 받았었는데 문제 난이도가 루비 V인 시점에서 눈치챘어야 했다;;문자 $X$가 정확히 하나씩 존재한다는 걸 생각하면 문자열 $A$, $B$ 모두 $X$가 위치하는 부분에서 끊어서 나눌 수 있다.$LCS(
53.BOJ 22856 | 트리 순회

중위 순회에 대해 물어보는 문제다. 이진 트리에서 중위 순회는 left -> parent -> right 순서로 탐색하는 방법이다.문제에서는 일반적인 중위 순회가 아닌 유사 중위 순회에서의 이동 횟수를 물어보고 있다.유사 중위 순회는 다음과 같이 진행된다.일반적인 중위
54.BOJ 11505 | 구간 곱 구하기
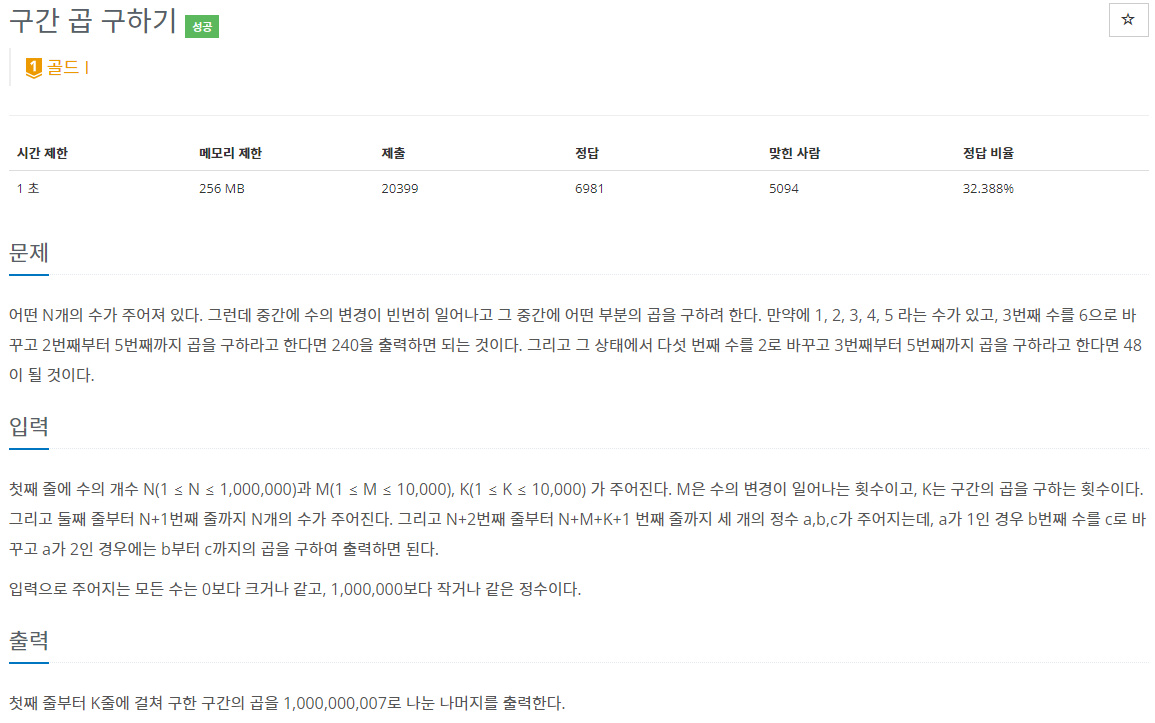
리프 노드부터 업데이트하는 세그트리를 만들 줄 아십니까? 라고 물어보는 문제다. 구간 합 구하기에서 update() 함수를 Top-down으로 만들었다면 이 문제에서는 0의 특수성 때문에 리프 노드부터 작동하도록 해야 한다.두 방법 모두 구현해보면 세그트리의 숙련도가
55.BOJ 5419 | 북서풍
스위핑의 어려움을 알려주는 문제라고 생각한다. 2차원 평면 위의 점 75000개를 순서대로 쓸어내려가면서 각 점마다 $O(logN)$으로 처리하는 문제다.어떤 섬에 대해서 그 섬보다 y좌표가 작고, x좌표가 큰 섬만 방문이 가능하다. 가장 먼저 생각나는 방법은 $O(N
56.BOJ 28020 | Attention
길이가 3인 LCS의 개수를 구하는 문제다. 이 문제는 길이가 3인 LIS를 구하는 문제로 치환할 수 있다.그러므로 길이가 3인 LIS를 구하는 방법을 생각해보자.길이가 3인 부분수열의 중앙값을 고정하고, front, middle, back 형태로 생각하자.front는
57.BOJ 5012 | 불만 정렬
= (\[코드
58.BOJ 24506 | blobpopcorn
아이디어성 문제라고 생각했는데 구현도 헷갈리고 어려웠습니다. 중간에 LIS라고 착각해서 이상한 길로 빠지기도 하고, 어떻게든 해설은 안 보려고 했지만 결국 멘붕와서 해설을 보게 만들었던 문제...아무튼 기본 아이디어는 스스로 떠올렸기 때문에 그나마 만족합니다.일단 이
59.BOJ 1078 | 뒤집음
요약 : 코딩을 못해도 시간을 박으면 누구나 풀 수 있다. 근성으로 가능한 플레 I 문제다! 근데 오래 걸린다.완전 수학 문제였는데 예제 입력과 출력이 잘 나와 있어서 풀기까지 시간은 많이 걸렸지만 틀렸습니다를 받진 않았다.교양 시간에 풀기 시작했는데 중간에 너무 많은
60.BOJ 1395 | 스위치
일단 이 문제는 $O(N^2/64)$로 뚫린다고 합니다. Bitset으로 날먹할 수 있습니다.스위치의 값은 0과 1 중 하나라는 점이 중요 포인트입니다. query() 가 합을 구하도록 되어 있으니 구간 합 세그트리를 구성해야 합니다. lazy는 boolean 값을 담
61.BOJ 13925 | 수열과 쿼리 13
길이가 N인 수열에서 4가지 쿼리를 적절하게 처리하는 문제입니다.구간 덧셈, 구간 곱셈, 구간 변경 연산과 구간 합을 출력하는 쿼리가 들어있습니다.구간 덧셈과 곱셈, 그리고 변경은 전부 update() 연산이고, lazy하게 처리하는 방법이 조금 떠올리기 어렵습니다.그
62.BOJ 28138 | 재밌는 나머지 연산

5월 월간 향유회 A번 문제입니다. 나머지 정리를 배웠다면 다음 식을 구성할 수 있습니다.$N = mq + R$따라서 $N - R$이 나누어 떨어지도록 하는 $m$을 찾으면 됩니다.단, $R$이 나머지여야 하므로 $m > R$ 이어야 합니다.$N-R$의 약수를 구하고,
63.BOJ 28139 | 평균 구하기

5월 월간 향유회 B번 문제입니다.우선 문제를 보면 머리가 아픕니다. 저는 조합론을 별로 안 좋아합니다. 그래도 문제를 봅시다.만약 고등학교 때 확률과 통계를 배웠다면 비슷한 문제를 내신에서 풀어봤을 것입니다.어떤 한 사람의 위치에서 출발해서 모든 사람의 위치를 방문하
64.BOJ 28140 | 빨강~ 빨강~ 파랑! 파랑! 달콤한 솜사탕!

5월 월간 향유회 C번 문제입니다.이건 이분탐색이 정해입니다. ㄹㅇ.구간 l, r이 주어질 때, 그 구간 내부에서 R과 B를 찾아야 합니다.R을 나타내는 인덱스 a, b와 B를 나타내는 인덱스 c, d가 있을 때, $a<b<c<d$인 a, b, c, d
65.BOJ 28086 | 미소녀 컴퓨터 파루빗토 쨩

아니 이게 참... 제목이... 파루빗토가 8비트라고 합니다. 알고 싶지 않았습니다.원래는 제목 때문에 올리기는 싫었는데 이걸 어렵게 푸시는 분들이 많아서 올려봤습니다.문제로 주어진 수식이 8진수 사칙연산이고, 그걸 10진수로 변환해서 더하고, 다시 8진수로 변환합니다
66.BOJ 28068 | I Am Knowledge
정답 비율이 지나치게 낮은 것이 눈에 띕니다. 그리고 그럴 만 합니다.이 문제는 정렬 후 순회하면서 $O(N)$에 처리하는 그리디의 전형적인 유형입니다. 그러나 정렬하는 과정이 생각이 많이 필요하고, 코드는 단순하나 생각이 단순하지 않은 문제입니다. 근데 풀고 나면 엄
67.BOJ 4386 | 별자리 만들기

최소 스패닝 트리를 그려서 해결하는 기초 문제다. 모든 별을 잇는 트리의 선분 길이를 출력하라는 문제인데 그냥 평범하게 구현해서 출력하자.여기서는 간선의 비용이 아닌 정점의 좌표가 주어지므로 잘 가공해서 간선으로 만드는데 $O(N^2)$이 들고, $N = 100$이기
68.BOJ 2662 | 기업투자
나는 내가 생각해도 심각한 정도의 DP 부족인데, 최근 열린 Codeforce Div 3에서 간단한 DP 문제를 BFS로 삽질하다가 40분 날리고 충격에 빠졌다.그래서 곧 있을 SUAPC와 각종 대회들에서 팀원들 발목은 잡지 않으려고 DP 연습을 하고 있다.월요일부터