백준 14003 가장 긴 증가하는 부분수열 5

문제링크

https://www.acmicpc.net/problem/14003

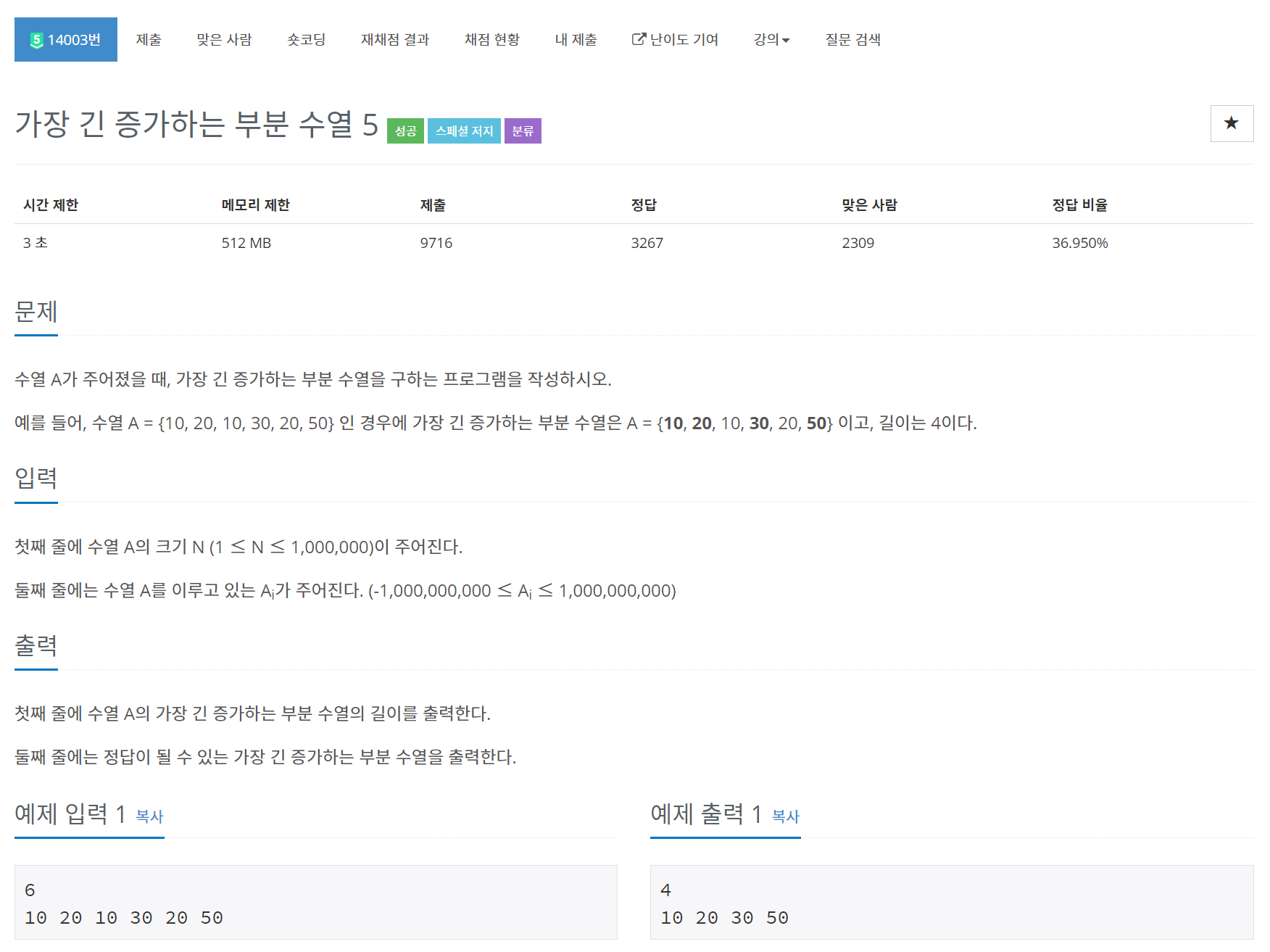
문제

풀이

가장 긴 증가하는 부분 수열 O(NlogN) + 경로추적 문제

기존의 LIS O(NlogN) 풀이에서 한 가지를 더 생각하면 된다.

값을 교체할 때 해당 index에서 가장 긴 증가하는 부분 수열의 길이
dp[i] = distance(v.begin(),arr[i]) + 1
이고 v.back()보다 arr[i]가 값이 더 크다면 dp[i]=v.size()+1 와 같다 는 것만 알고 나면 나머지 풀이는 간단하다.

코드

#include <iostream>
#include <vector>
#include  <algorithm>
using namespace std;
#define INF 2147483647
vector<int> v;
int dp[1000001], arr[1000001];
int n, cnt = 1;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	v.push_back(INF);
	for (int i = 0; i < n; i++) cin >> arr[i];
	for (int i = 0; i < n; i++) {
		if (arr[i] > v.back()) {
			v.push_back(arr[i]);
			dp[i] = ++cnt;
		}
		else {
			auto it = lower_bound(v.begin(), v.end(), arr[i]);
			*it = arr[i];
			dp[i] = distance(v.begin(), it) + 1;

		}
	}

	cout << v.size() << '\n';

	vector<int> ans;
	for (int i = n - 1; i >= 0; i--) {
		if (dp[i] == cnt) {
			cnt--;
			ans.push_back(arr[i]);
		}
	}


	for (int i = ans.size() - 1; i >= 0; i--) {
		cout << ans[i] << ' ';
	}



}

후기(정리)

dp는 아직도 헷갈린다.

+)
distance 함수를 처음 사용해봤다.
iterator 사용 시 해당 iterator 가 가리키는 원소가 몇 번째 index 인지 구할 때 편리하다. distance(v.begin(),it);