문제링크
https://www.acmicpc.net/problem/1670
문제
풀이
어느 한 사람을 기준으로 잡고 각 사람들과 악수하는 경우를 나눠서 생각해보자.
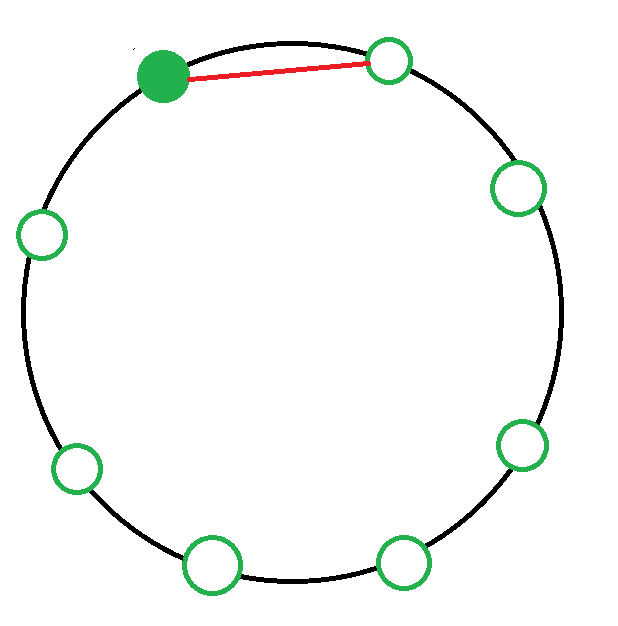
1. 시계방향으로 한 칸 떨어진 사람과 악수하는 경우
직선을 기준으로 두영역으로 나누어 지는데 한쪽 영역은 사람이 0명이고 다른쪽은 6명이다.
경우의 수 : dp[0] x dp[6]
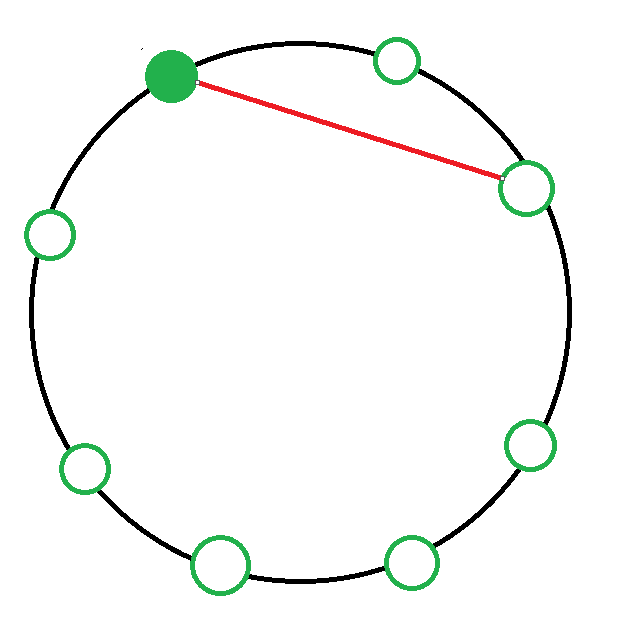
2. 시계방향으로 두 칸 떨어진 사람과 악수하는 경우
마찬가지로 두 영역으로 나누어 지는데 각 영역의 사람들이 홀수이므로 모든 사람이 악수할 수 있는 경우는 없다.
경우의 수 : 0
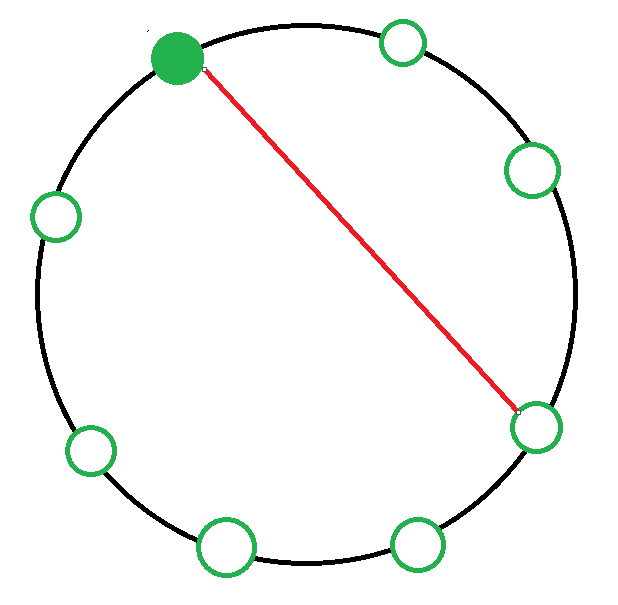
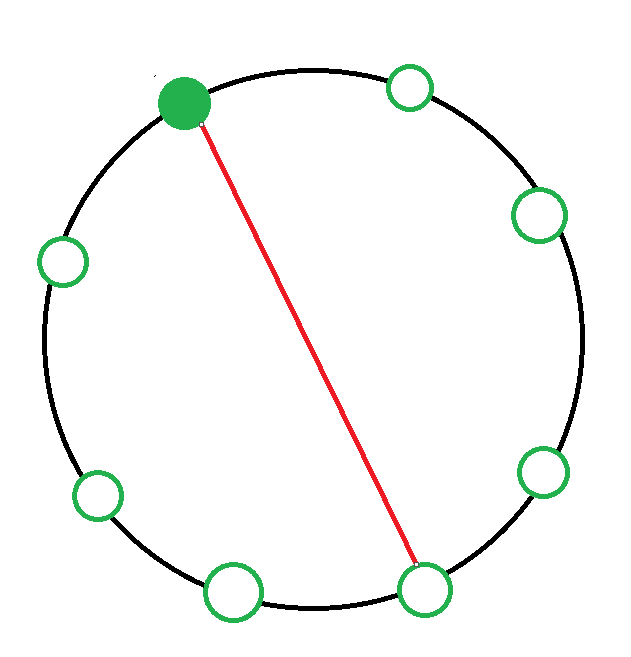
3. 시계방향으로 세 칸 떨어진 사람과 악수하는 경우
경우의 수 : dp[2] x dp[4]
4. 시계방향으로 네 칸 떨어진 사람과 악수하는 경우
경우의 수 : 0
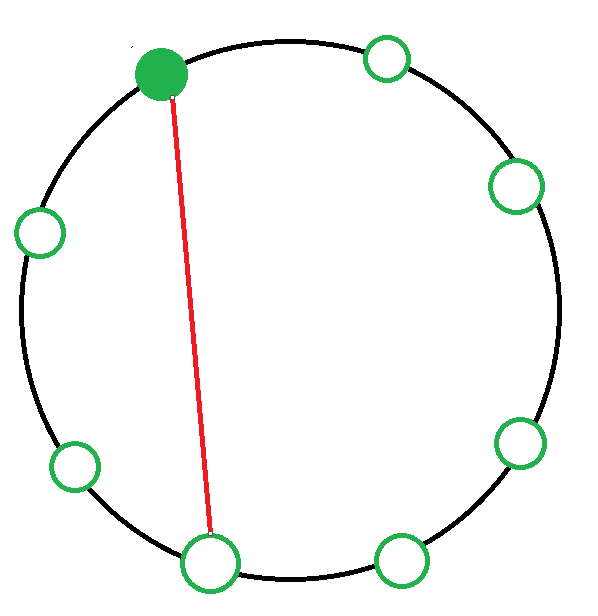
5. 시계방향으로 다섯 칸 떨어진 사람과 악수하는 경우
경우의 수 : dp[4] x dp[2]
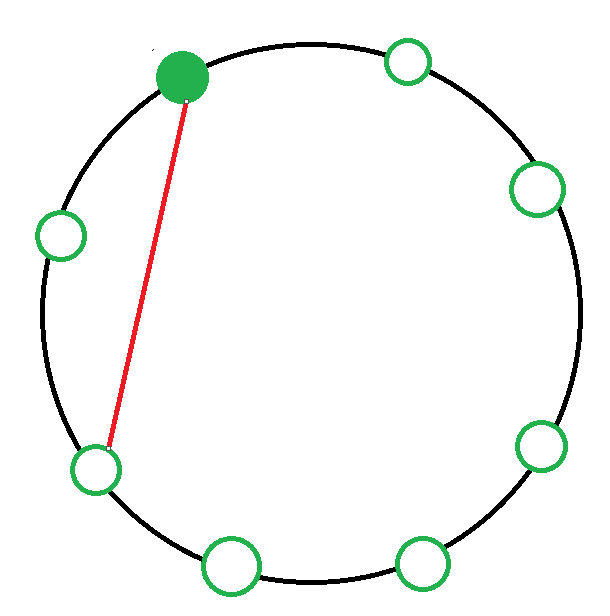
6. 시계방향으로 여섯 칸 떨어진 사람과 악수하는 경우
경우의 수 : 0
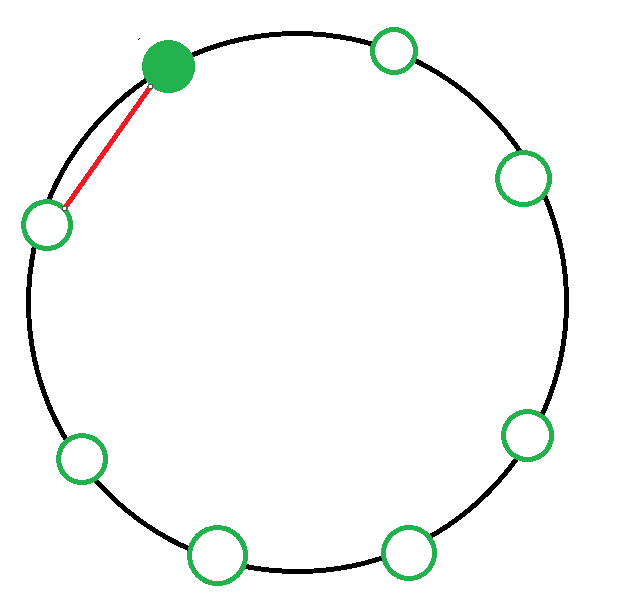
7. 시계방향으로 일곱 칸 떨어진 사람과 악수하는 경우
경우의 수 : dp[6] x dp[0]
dp[8] = (dp[0] x dp[6]) + (dp[2] x dp[4]) + (dp[4] x dp[2]) + (dp[6] x dp[0])
dp[n] = (dp[0] x dp[n-2]) + (dp[2] x dp[n-4]) + ... +(dp[n-2] x dp[0] )
코드
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
#define MOD 987654321
typedef long long ll;
ll dp[10001];
int main(void) {
int n;
cin >> n;
dp[2] = dp[0] = 1;
for (int i = 4; i <= n; i += 2) {
for (int j = 2; i - j >= 0; j += 2) {
dp[i] = (dp[i] + (dp[j-2] * dp[i - j]) % MOD) % MOD;
}
}
cout << dp[n];
}후기
평소 dp문제에 너무 약해서 지레 겁먹었는데 이 문제는 그나마 풀만했다. 골드2 이기는 한데 저번에 풀었던 색상환 문제가 더 어렵게 느껴진다.
