Linear Regression (선형 회귀)
Simple Linear Regression
경력과 연봉이라는 단순 선형 관계에 존재하는 데이터셋의 관계를 살펴보고 경력에 대한 연봉을 예측해보자.
DataSet
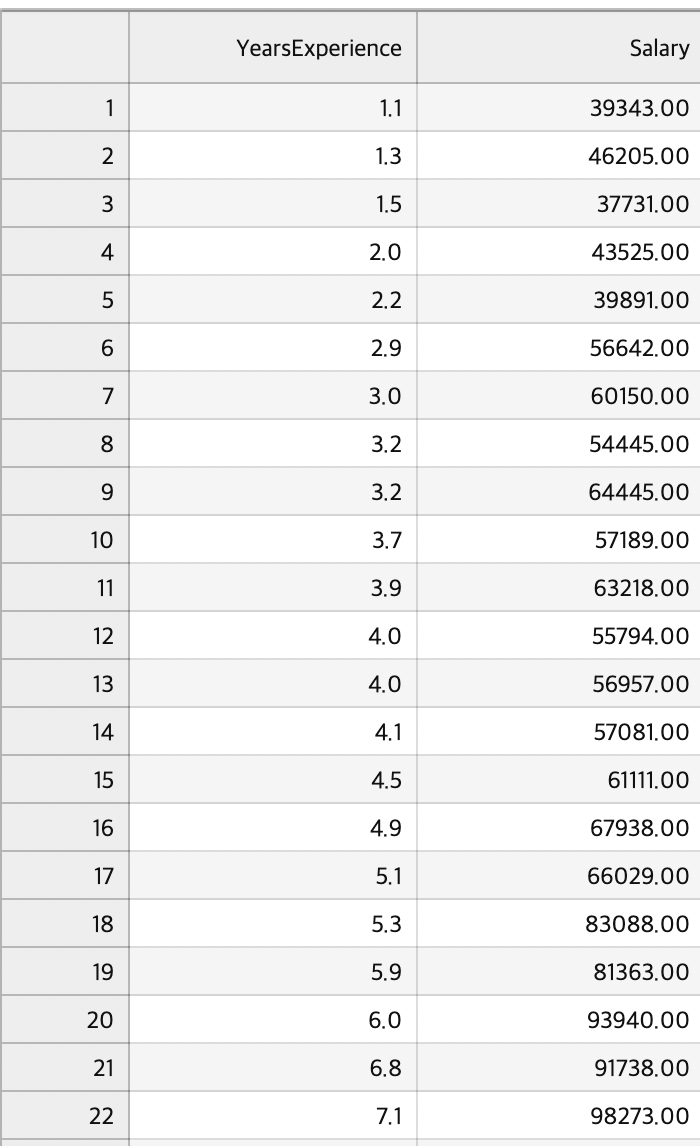
dataset = pd.read_csv('Salary_Data.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values- iloc"은 "integer location"의 약자로, 정수 기반의 위치 인덱싱을 의미
- data.iloc[행선택, 열선택]
데이터프레임에서 iloc을 사용하여 특징 행렬을 추출합니다. 여기서 [:, :-1]은 모든 행을 선택하면서 마지막 열을 제외한 모든 열을 선택하는 것을 의미한다 (즉, 경력에 해당하는 부분)
[:, -1]은 모든 행을 선택하면서 마지막 열만 선택하는 것을 의미한다. 이렇게 선택된 대상 변수는 NumPy 배열로 변환되어 y에 할당된다.
테스트셋, 데이터셋 분할하기
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)test_size를 0.2로 둔다는 것은 트레이닝을 해당 데이터셋의 8할만큼 할당하고 테스트로는 2할 할당하겠다는 의미.
트레이닝 시키기
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)LinearRegression 모델을 활용해 regressor 객체를 생성하자.
fit 메소드를 통해 트레이닝 셋으로 할당한 데이터를 활용해 말 그대로 훈련을 시켜보자
X_train은 훈련 데이터의 특징 행렬이고, y_train은 대상 변수(목표값)이다. 모델은 주어진 특징과 대상 변수 간의 관계를 학습하여 모델 파라미터를 조정한다.
테스트 셋을 활용한 결과 예측
우리의 목적은 경력에 대한 데이터를 가지고 연봉을 예측하는 일이기에 X_test에 할당된 경력의 정보를 인자로 넣어 연봉을 예측해보자
y_pred = regressor.predict(X_test)테스트 데이터에 대한 예측을 수행한다. X_test는 모델이 이전에 보지 않은 새로운 데이터의 특징 행렬이며, 모델은 이를 사용하여 예측값을 계산한다. 예측된 결과는 y_pred에 저장된다.
y_pred에는 모델이 테스트 데이터에 대해 예측한 값들이 저장되어 있다. 이 예측값을 실제 테스트 데이터의 실제 값과 비교하여 모델의 성능을 평가할 수 있다.
트레이닝 셋 시각화
plt.scatter(X_train, y_train, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience (Training set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show실제 관계 (트레이닝 셋)
plt.scatter(X_train, y_train, color='red'): 훈련 데이터의 산점도를 그린다. X_train은 훈련 데이터의 특징(경력), y_train은 대상 변수(연봉)이다. 각 데이터 포인트는 빨간색으로 표시된다.
예측 모델
plt.plot(X_train, regressor.predict(X_train), color='blue'): 훈련 데이터에 대한 선형 회귀 모델의 예측 결과를 선 그래프로 그립니다. X_train에 대한 예측값은 regressor.predict(X_train)로 계산되며, 이를 통해 학습된 모델이 훈련 데이터에 어떻게 적합되었는지를 시각적으로 확인할 수 있다. 선은 파란색으로 표시된다.
테스트 셋 시각화
plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience (Test set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.showplt.scatter(X_test, y_test, color='red'): 테스트 데이터의 실제 값에 대한 산점도를 그린다. X_test는 테스트 데이터의 특징(경력), y_test는 대상 변수(연봉)이다. 각 데이터 포인트는 빨간색으로 표시된다.
이를 통해 모델이 테스트 데이터에 얼마나 잘 일반화되었는지를 시각적으로 확인할 수 있다.
BONUS
우리는 기존에 갖춰진 데이터셋을 활용해 트레이닝/테스트 셋을 나누어 예측모델을 세웠다. 그렇다면 데이터셋에 존재하지 않는 가령, 12년 경력을 가진 사람의 연봉은 어떻게 예측 할 수 있을까?
print(regressor.predict([[12]]))위에서 중요한 점은 predict 메소드를 사용할 땐 2차원 배열로 넣어야 한다. 2차원 배열은 대괄호를 두 번 씌우면 된다. X_test 역시 아래처럼 2차원 배열로 구성되어 있다.

그러면 아래와같이 연봉을 예측한다.
선형 모델 방정식 및 상관 계수 확인
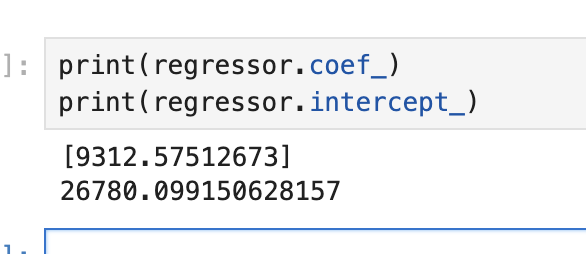
print(regressor.coef_)
print(regressor.intercept_)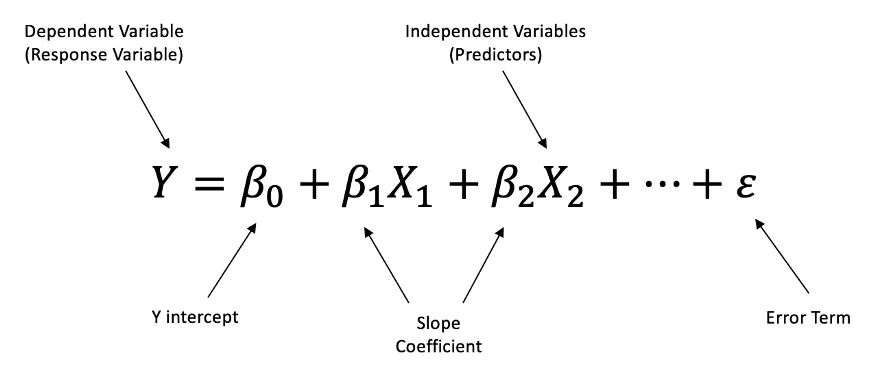
우리의 단순 선형 회귀 모델의 방정식은 다음과 같다.
Salary=9345.94×YearsExperience+26816.19
coefficient는 상관계수로서, 모델의 기울기(coefficients 또는 weights)를 나타낸다. 이 값은 특징(독립 변수)에 대한 회귀 계수이다.
interceptor 값은 모델의 절편(intercept)을 나타낸다. 이 값은 특징이 0일 때의 예측값이다. (y절편)
Multiple Linear Regression (다중 선형 회귀)
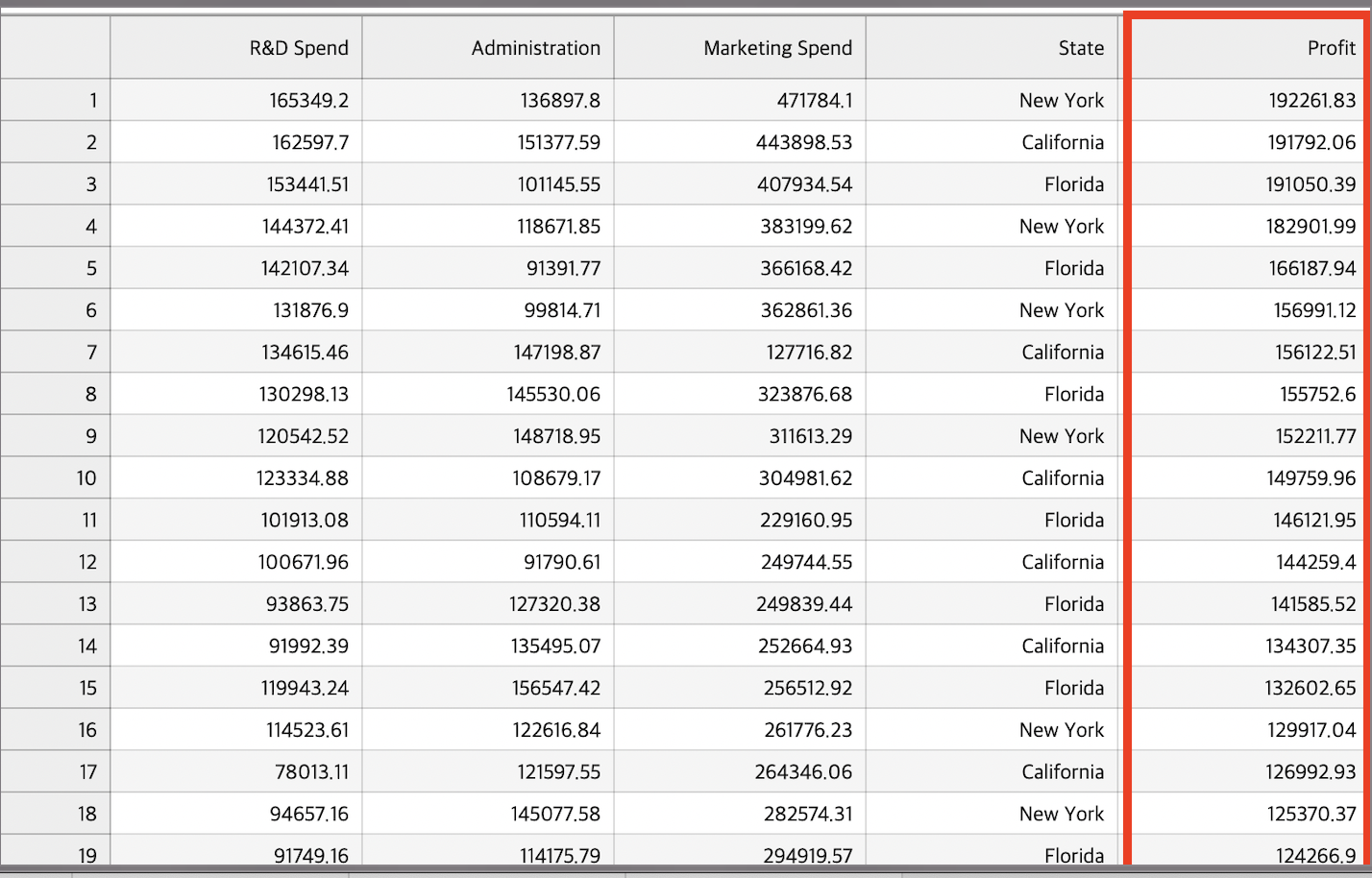
다중 회귀 분석은 예측변수(독립변수)가 2개 이상인 회귀 분석
다중 회귀 분석에는 변수가 많을 수록 적절한 회귀 모형 선택 필요
회귀모형에 포함되는 독립변수 선택 기준
- 종속변수와 높은 상관관계
- 선택된 독립변수들은 서로 낮은 상관관계 지님 (다중공전성 회피 위함)
- 독립변수의 수는 적을 수록 유리
독립변수 선택 방법
1. All-in Cases
- 모든 변수를 동원해서 모델 예측
2. Backward Elimination
- 모든 변수 중 불필요한 변수를 제거해 나가는 방식
- 중요 변수가 제외될 가능성이 적음 (안정성)
- 이미 제외한 변수는 재선택 X
3. Forward Selection
- 기여도가 높은 변수부터 하나씩 추가
- 빠른 계산이 장점
- 이미 선택된 변수는 제외되지 않음
DataSet
다음과 같은 독립변수/종속변수 형태의 데이터셋이 존재하고 우리의 목표는 독립변수를 통한 profit 예측이다.
특이점은 State경우 categorical variane이기에 one-hot-encoding을 적용할 것이다.
범주형 데이터 인코딩하기
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
# 범주형 데이터를 가지고 있는 열에 one-hot-encdoing 수행
ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])], remainder='passthrough')
X = np.array(ct.fit_transform(X))ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])], remainder='passthrough'): ColumnTransformer를 생성합니다. 여기서('encoder', OneHotEncoder(), [3])의 의미는 4번째 열(인덱스 3)에 대해서만 One-Hot Encoding을 수행하도록 지정한다. 'encoder'는 이 변환을 구분하는 이름이다.
remainder='passthrough': 나머지 열은 그대로 유지하도록 지정
X = np.array(ct.fit_transform(X)): ColumnTransformer를 사용하여 입력 데이터 X에 변환을 적용하고, 결과를 다시 NumPy 배열로 저장한다. 이 때, 3번째 열이 One-Hot Encoding으로 변환되며, 나머지 열은 그대로 유지된다.
검증/테스트 데이터셋 분할하기
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)훈련 시키기
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)테스트셋을 활용한 모델 예측 수행
y_pred = regressor.predict(X_test)
np.set_printoptions(precision=2)
print(np.concatenate((y_pred.reshape(len(y_pred), 1), y_test.reshape(len(y_test), 1)), axis=1))y_pred = regressor.predict(X_test): 테스트 데이터인 X_test에 대한 예측값을 모델에서 계산하여 y_pred에 저장한다.
np.set_printoptions(precision=2): NumPy의 출력 형식을 설정하여 소수점 이하 2자리까지만 출력되도록 한다.
y_pred.reshape(len(y_pred), 1): y_pred 배열을 2D 배열로 변환한다. 이렇게 하는 이유는 나중에 np.concatenate 함수를 사용하기 위함.
y_test.reshape(len(y_test), 1): y_test 배열도 2D 배열로 변환한다.
np.concatenate((y_pred.reshape(len(y_pred), 1), y_test.reshape(len(y_test), 1)), axis=1): y_pred와 y_test를 수평으로(concatenate) 결합한다. 이를 통해 예측값과 실제값이 나란히 배열되어 출력된다. axis=1은 수평 방향으로 결합하라는 의미이다.
BONUS
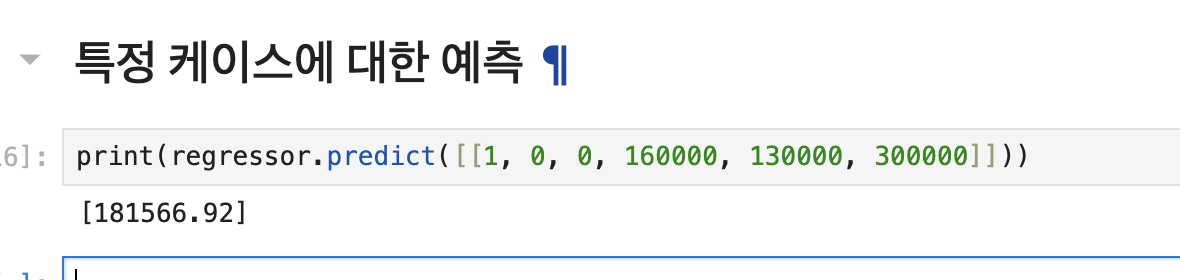
Q1. 특정 케이스에 대해 예측모델에 어떻게 적용하면 좋을까?
print(regressor.predict([[1, 0, 0, 160000, 130000, 300000]]))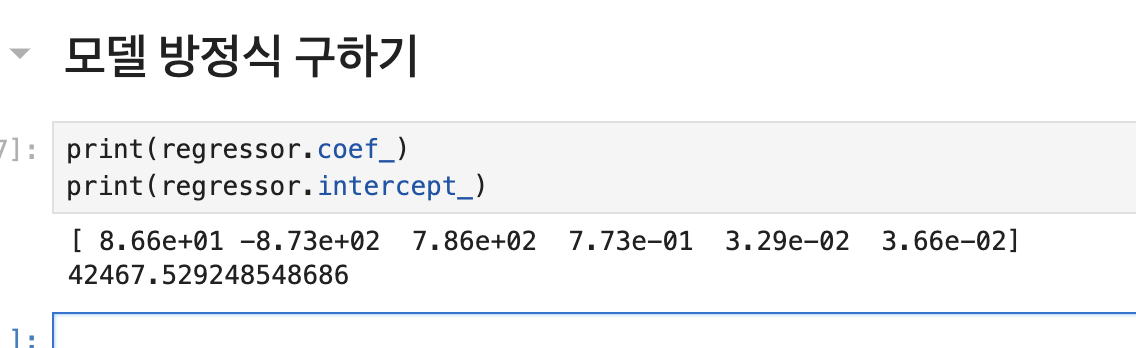
- 특이점 1: prdict 메소드는 2차원 배열만을 파라미터로 받기에 대괄호 2개를 사용해야함
- 특이점 2: categorcial data의 경우 원-핫 인코딩을 적용했기에 특정 범주형에 해당하는 데이터의 원-핫 인코딩 값을 '앞'에 입력해야함 (1, 0, 0)
Q2. 다중 선형 회귀 모델의 방정식은 어떻게 구할까?
다중 선형 회귀 모델의 방정식은 다음과 같다.
Profit=86.6×Dummy State 1−873×Dummy State 2+786×Dummy State 3+0.773×R&D Spend+0.0329×Administration+0.0366×Marketing Spend+42467.53각 범주형 카테고리에 속하는 변수마다 상관계수가 있을 것이고, 해당 상관계수와 범주형 데이터를 곱하고 상수항을 더한다.
구체적으로 위의 상관계수를 해석해보자면 위의 데이터셋 기준 앞의 상관계수들은 뉴욕, 캘리포니아, 플로리다를 의미하고 뒤의 3가지 상관계수는 R&D비용, 등록비용, 마켓팅 비용에 대한 상관정도를 의미한다.
뉴욕과 플로리다는 양의 상관계수를 의미하기에 profit 산출함에 있어 해당 범주에 속할 경우, 이익이 증가하는 경우고 캘리포니아에 속한 경우 이익이 감소한다.
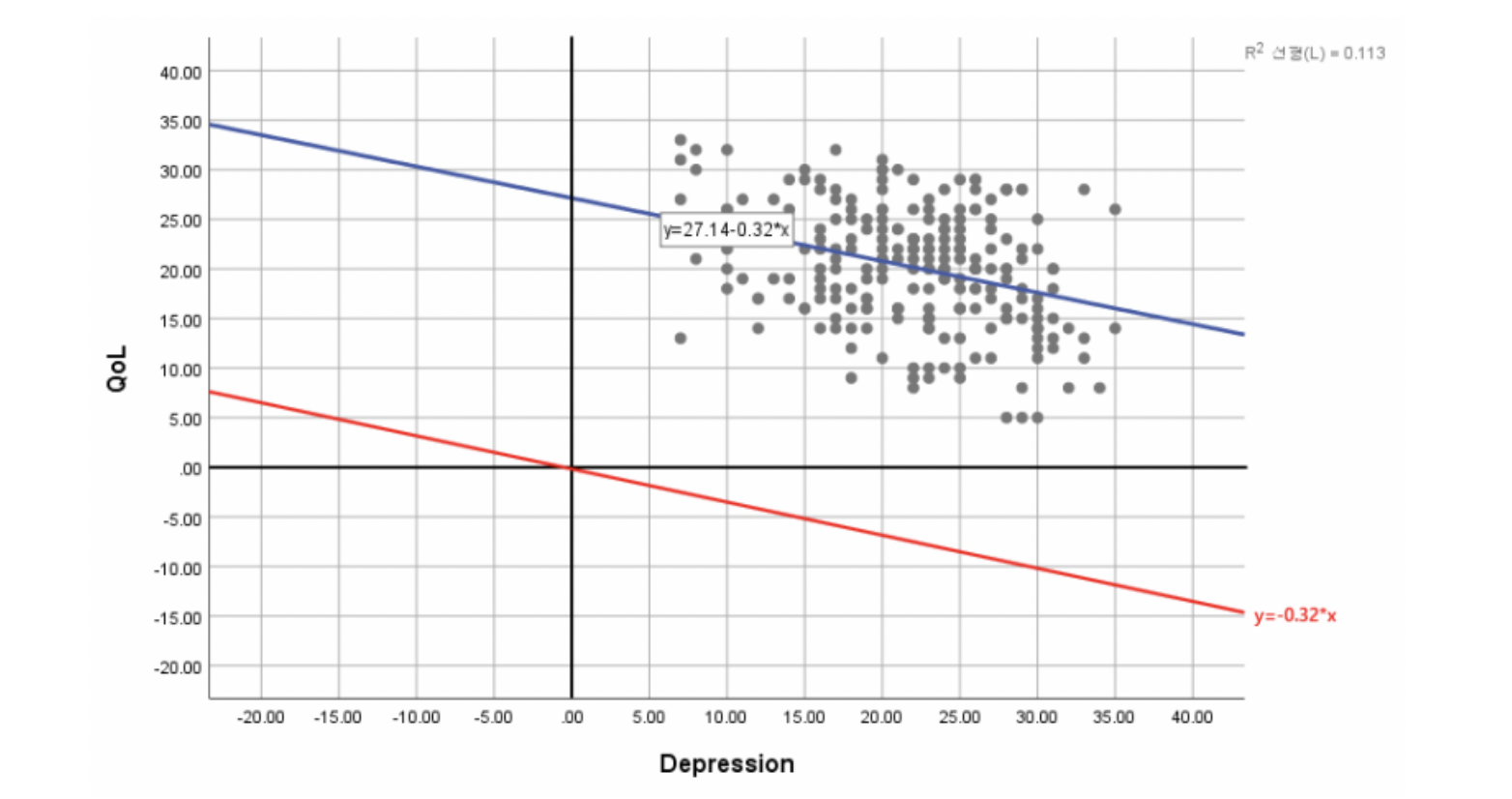
마지막으로 상수항(Intercept)을 기입해야 하는 이유는 아래의 그래프에서 확인할 수 있는데, 상수항을 기재하지 않을 시 해당 모델의 유의성과 관계없이 전체 데이터에 대한 적합한 회귀선을 그을 수 없다. 즉, 아래 그래프 기준 과소 추정의 결과를 얻을 수 있는 것이다.
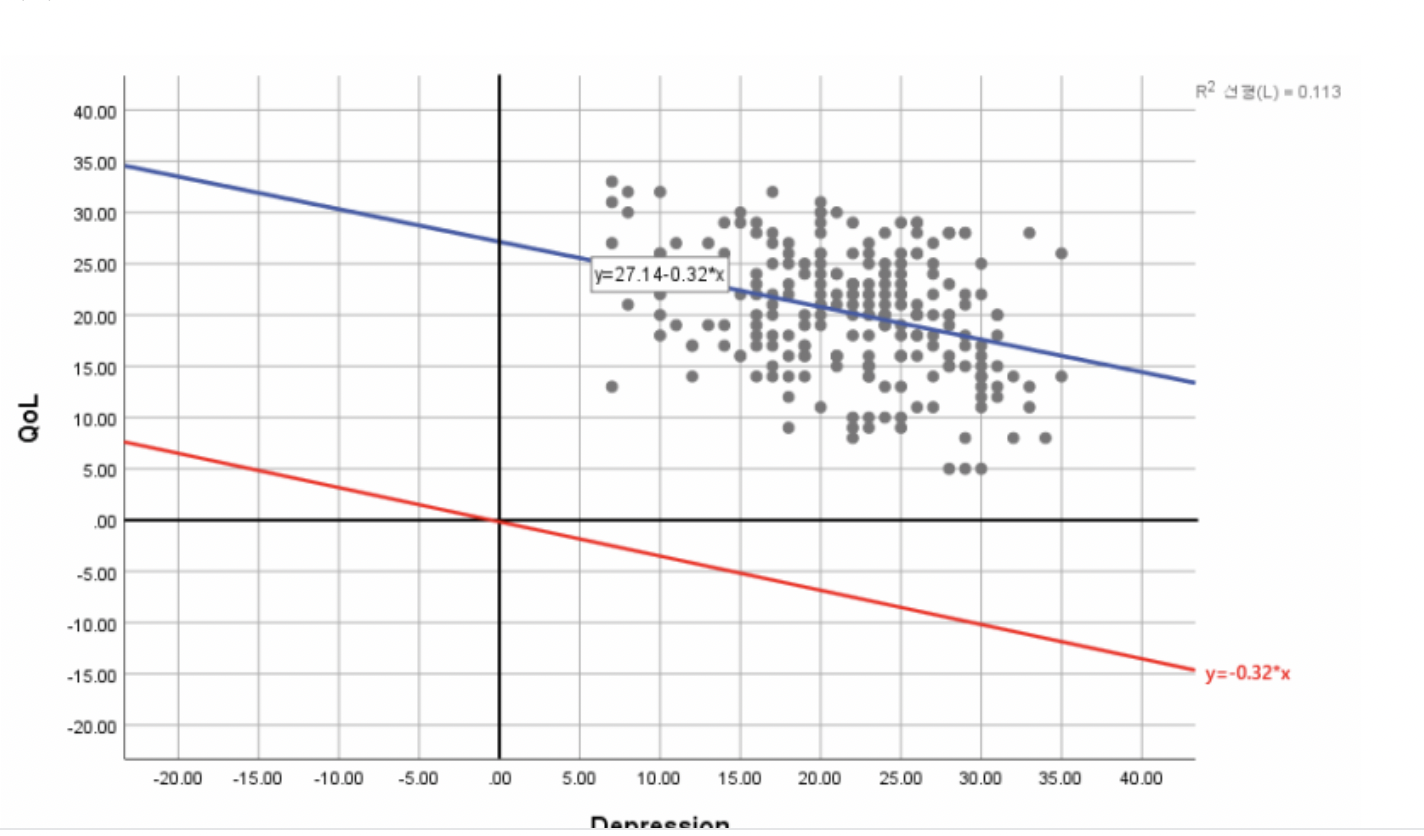
https://m.blog.naver.com/sharp_kiss/222639216626
Polynomial Regression (다항식 선형 회귀)
아래 사진처럼 데이터가 단순한 선형성을 지니지 않고 다항식 형태의 관계를 지녔다면 다항식 선형 회귀를 고려해봐야 한다.
아래 예시에서는 경력에 대한 연봉 측정을 위한 모델을 세울 것이다.
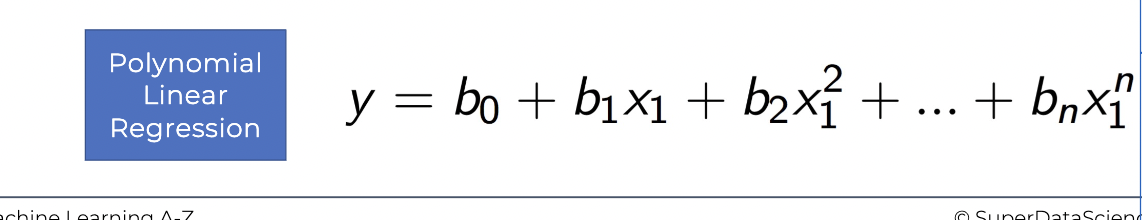
Importing LB
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdImporting DataSet
dataset = pd.read_csv('Position_Salaries.csv')
#Level
X = dataset.iloc[:, 1:-1].values
#Salary
y = dataset.iloc[:, -1].values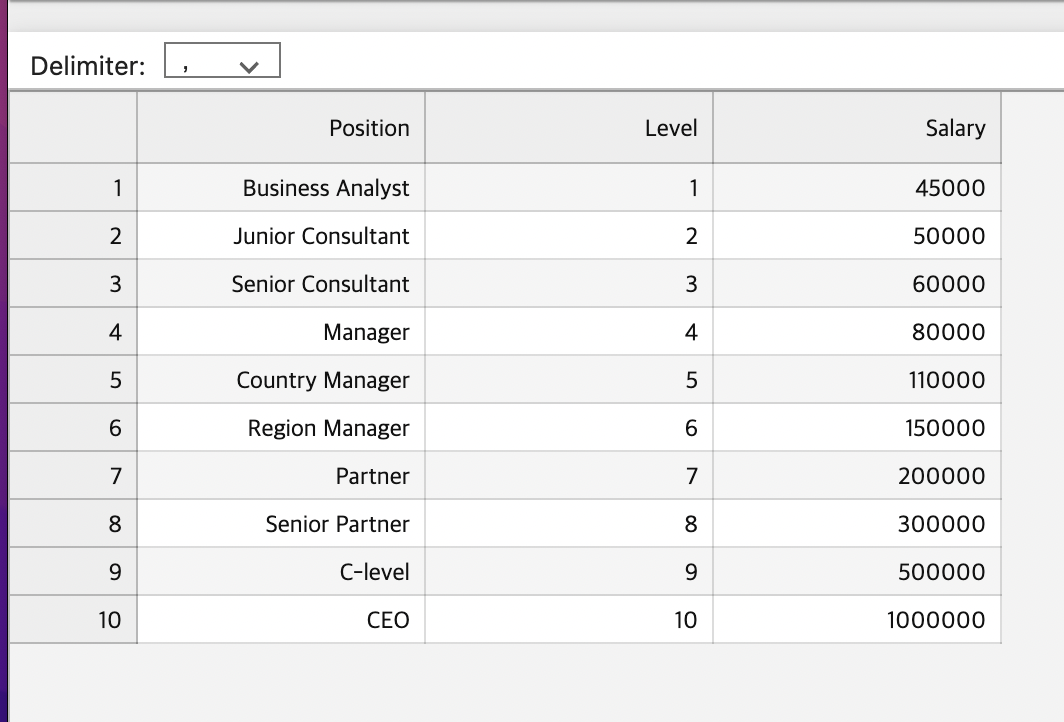
Training the Linear Regression model on the whole dataset
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)fit 메서드를 사용하여 선형 회귀 모델을 주어진 데이터 X와 대응하는 종속 변수 y에 대해 훈련시킨다.
Training the Polynomial Regression model on the whole dataset
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=4)
# 다형식 형태로 변환
X_poly = poly_reg.fit_transform(X)
lin_reg2 = LinearRegression()
# 선형 회귀 함수로 concat
lin_reg2.fit(X_poly ,y)PolynomialFeatures 클래스의 인스턴스를 생성한다. degree=4는 다항식의 차수를 나타내며, 여기서는 4차 다항식을 사용할 예정이다.
fit_transform 메서드를 사용하여 주어진 입력 데이터 X를 다항식 형태로 변환한다. (X_ploy)
다항식 형태로 변환된 데이터 X_poly와 대응하는 종속 변수 y를 사용하여 선형 회귀 모델을 훈련시킨다.이는 위에서 생성한 다항식 형태의 특성을 사용하여 비선형 관계를 감지하고 모델을 훈련시키는 과정이다.
Visualizing the Linear Regression Results
plt.scatter(X,y, color = 'red')
plt.plot(X, lin_reg.predict(X), color = 'blue')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()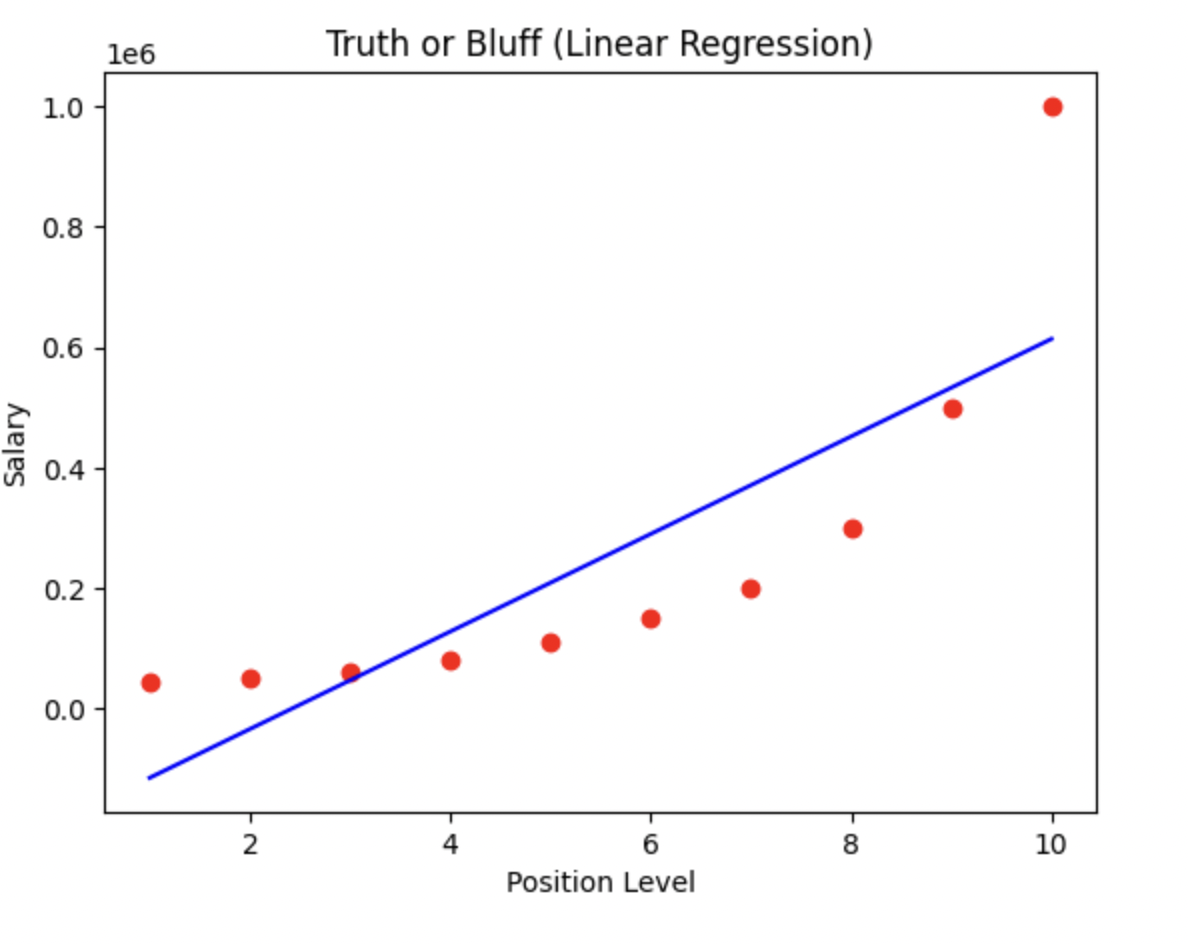
위의 결과를 통해 볼 수 있듯이 단순 선형 회귀 모델을 사용해 연봉 측정을 할 경우 정확한 예측 모델을 세우기 어렵다.
Visualizing the Polynomial Regression Results
plt.scatter(X,y, color = 'red')
plt.plot(X, lin_reg2.predict(poly_reg.fit_transform(X)), color = 'blue')
plt.title('Truth or Bluff (Polynomail Regression)')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()poly_reg.fit_transform(X)를 통해 입력 데이터 X를 다항식 형태로 변환하고, lin_reg2.predict를 사용하여 예측을 수행한다.
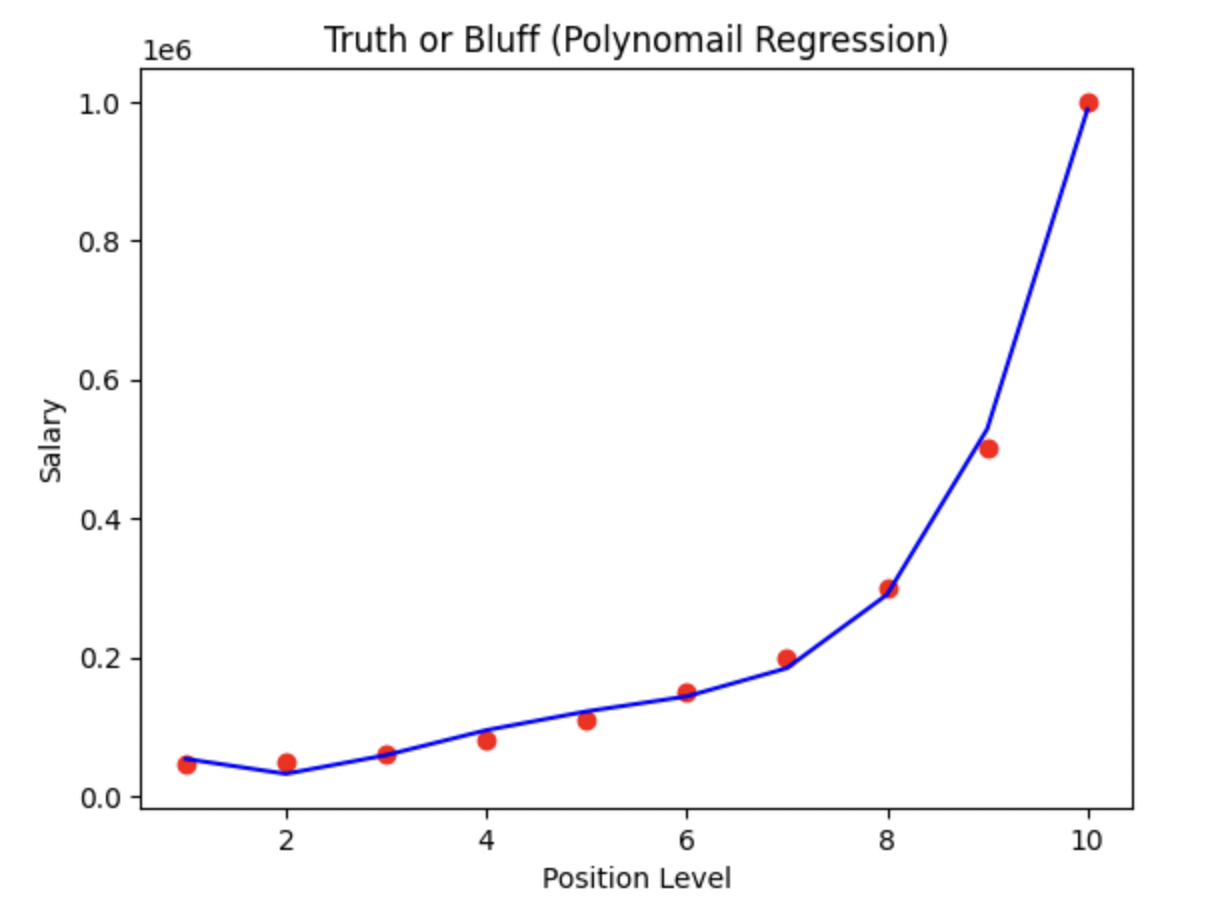
새로운 데이터로 결과 예측하기
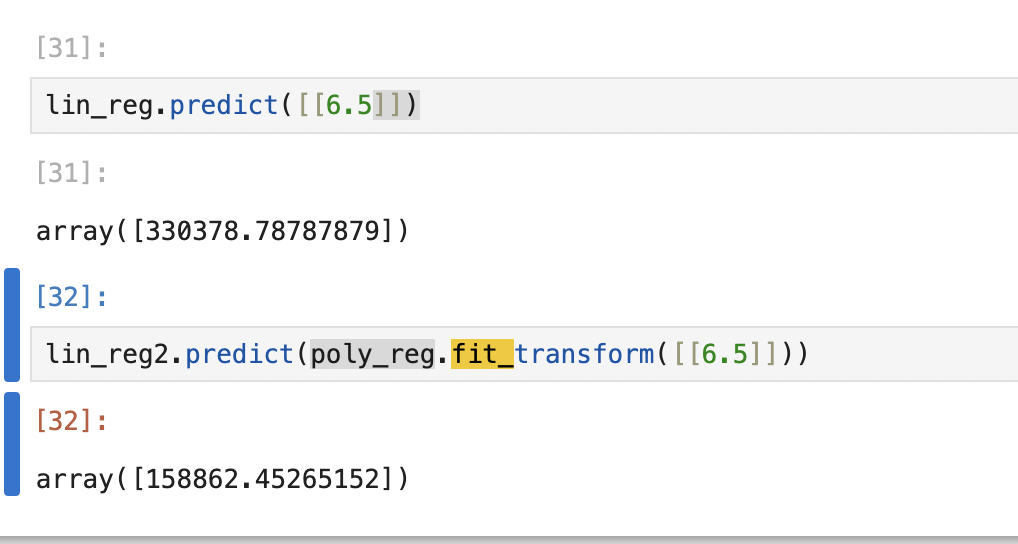
위와같이 단순 선형모델에서는 6.5의 위치(LEVEL)를 가지고 있는 사람에게 33만불의 연봉이 측정되는 과한 상황이 연출되지만 아래의 Polynomial을 적용시킨 모델의 예측결과는 합리적인 수준의 결과를 반환하는 걸 확인할 수 있다.
SVR (Support Vector Regression)
SVR은 회귀식이 추정되면 회귀식 위아래 2ϵ(−ϵ,ϵ)
만큼 튜브를 생성하여, 아래 그림에서처럼 튜브내에 실제 값이 있다면 예측값과 차이가 있더라도 용인해주기 위해 penalty를 0으로 주고, 튜브 밖에 실제 값이 있다면 C의 배율로 penalty를 부여하게 된다. 회귀선에 대해 일종의 상한선, 하한선을 주는 셈이다.
“SVR은 데이터에 노이즈가 있다고 가정하며, 이러한 점을 고려하여 노이즈가 있는 실제 값을 완벽히 추정하는것을 추구하지 않는다. 따라서 적정 범위(2ϵ) 내에서는 실제값과 예측값의 차이를 허용한다.”
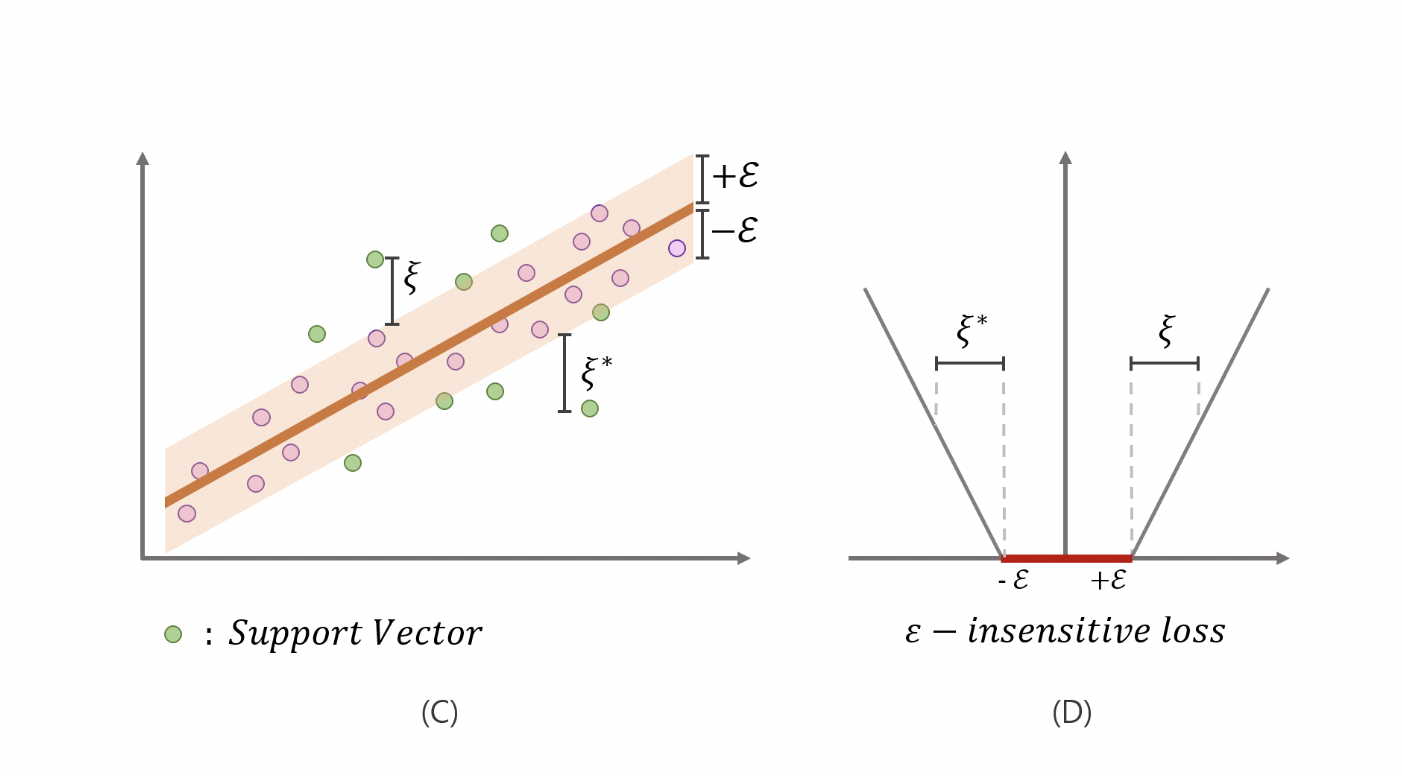
https://leejiyoon52.github.io/Support-Vecter-Regression/
Importing DataSet
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values- print(y) 시 일차원 배열로 나타나기에 y = y.reshape(len(y), 1) 코드를 통해 2차원 배열 형태로 변형시킨다.
len(y)는 y 배열의 길이를 나타내며, 1은 결과적으로 생성될 2D 배열의 형태를 나타냅니다. 여기서는 열(column)의 개수가 1인 2D 배열을 생성하게 된다.

Feature Scaling
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
sc_y = StandardScaler()
X = sc_X.fit_transform(X)
y = sc_y.fit_transform(y)범주형 데이터일 경우, 원-핫 인코딩을 통해 인코딩시켜주지만 해당 데이터의 경우 종속변수 역시 numerical한 특징을 지니므로 동시에 표준화를 진행한다.
sc_X, sc_y로 별개의 객체를 생성해 표준화를 진행하는 이유는 입력 데이터와 출력 데이터의 특성 스케일이 다를 때, 각각 따로 표준화를 수행하여 입력과 출력 간의 스케일 차이를 조절하기 위함이다.
전체 데이터 SVR 모델로 훈련시키기
from sklearn.svm import SVR
regressor = SVR(kernel = 'rbf')
regressor.fit(X,y)SVR은 주어진 데이터를 고차원 공간으로 매핑하여 비선형 관계를 모델링하는데 사용된다. kernel 매개변수는 데이터를 고차원으로 매핑할 때 사용되는 커널 함수를 지정한다. 여기서는 RBF 커널을 사용했으며, 이는 기존 특성 공간을 고차원 특성 공간으로 매핑하여 비선형 관계를 표현한다.
Feature Space Conversion (공간변환)
- 특징공간 변환은 기계 학습의 핵심 연산
- 원래 특징 공간을 목적 달성에 더 유리한 새로운 공간을 변환하는 작업
- EX) MLP에서 은닉층을 이용한 특징 공간 변환을 통해 XOR 문제 해결
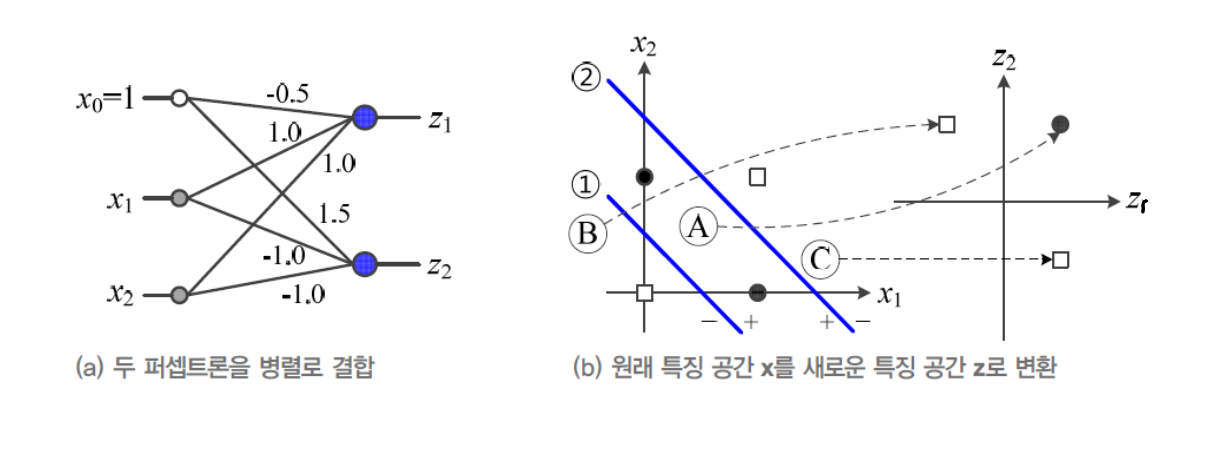
즉, 선형 분리 불가능한 입력 데이터를 다른 공간으로 매핑해 "선형 분리" 가능하도록 만드는 것이 목표
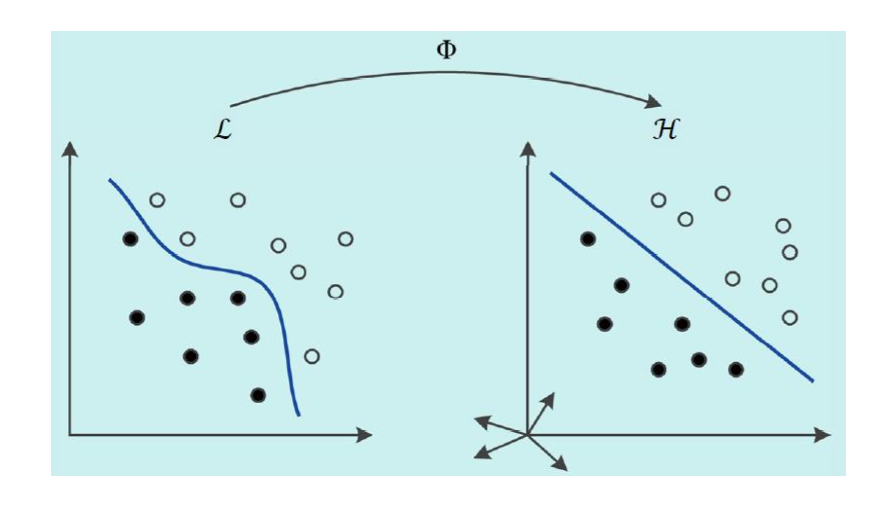
RBF 커널
이 커널은 가우시안 함수의 형태를 가지며, 데이터를 고차원으로 매핑하여 비선형 관계를 표현한다.
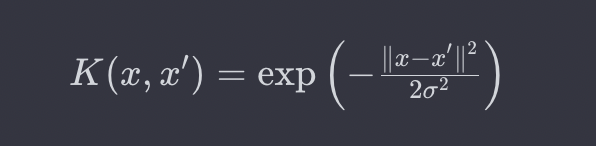
x, x`는 입력데이터 포인트이다.
오메가는 가우시안 함수의 폭을 조절하는 매개변수이다.
RBF 커널은 데이터 포인트 간의 유사도를 측정한다. 두 데이터 포인트 간의 거리가 가까울수록 유사도가 커지며, 멀리 떨어져 있을수록 유사도가 작다. 이러한 유사도를 통해 데이터를 고차원으로 매핑하여 선형 분리 가능한 상황을 만들 수 있다.
새 데이터에 대한 결과 예측
sc_y.inverse_transform(regressor.predict(sc_X.transform([[6.5]])).reshape(-1,1))c_X.transform([[6.5]]): 새로운 입력값 6.5를 현재 모델에 맞게 스케일링한다.
sc_y.inverse_transform(...): 예측 결과를 원래의 스케일로 역변환한다. sc_y는 타겟 변수에 대한 표준화를 수행한 스케일러이다.
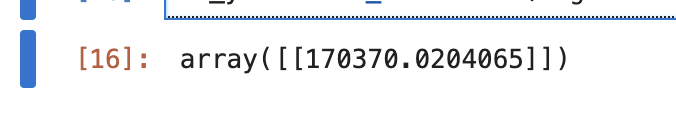
결과 상, 6.5 레벨을 지닌 사람에게 17만불의 연봉이 적당하다는 결과가 나온다.
시각화 하기
plt.scatter(sc_X.inverse_transform(X), sc_y.inverse_transform(y), color = 'red')
plt.plot(sc_X.inverse_transform(X), sc_y.inverse_transform(regressor.predict(X).reshape(-1,1)), color = 'blue')
plt.title('Truth of Bluff (SVR)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()sc_y.inverse_transform(y), color='red'): 원래 스케일로 변환된 훈련 데이터를 산점도로 표시한다. sc_X.inverse_transform(X)는 입력 특성을 원래 스케일로 변환하고, sc_y.inverse_transform(y)는 타겟 변수를 원래 스케일로 변환하다.
plt.plot(sc_X.inverse_transform(X), sc_y.inverse_transform(regressor.predict(X).reshape(-1,1)), color='blue'): SVR 모델을 사용하여 훈련 데이터에 대한 예측을 수행하고, 그 결과를 원래 스케일로 변환한다. 이는 모델이 훈련 데이터에 어떻게 적합되었는지를 시각적으로 보여준다.
