지금까지 우리는 정수형 변수만 알아보았다. 다음으로는 부동 소수점수를 알아보겠다. '부동'은 안 움직인다는 뜻도 있지만, 여기서는 물이나 공기 중에 떠서 움직인다는 의미이다. 따라서 부동 소수점수는 소수점이 자유롭게 움직인다는 뜻이다.
부동 소수점수를 쓰려면 기존의 자료형과 다른 자료형이 필요하다. 주로 float, double, long double을 쓴다. 각각 일반적으로 32비트, 64비트, 80, 96, 128 비트이다.
다음은 부동 소수점수의 여러 표현 방식이다.
double numberA = 9.0;
double numberB = 89.71e-1;
double numberC = 52.343E+2;실행 결과.

기본적으로 소수점 뒤의 0은 출력하지 않는다.
float과 double은 정밀도 면에서 차이를 보인다. 다음과 같은 예제를 보자.
cout.setf(ios_base::fixed, ios_base::floatfield); // 소수점 뒤 0을 출력해줌.
float numberA = 10.0 / 3.0;
double numberB = 10.0 / 3.0;
const float million = 1.0e6;
cout << "numberA = " << numberA << endl;
cout << "numberB = " << numberB << endl;
cout << "numberA * million = " << numberA * million << endl;
cout << "numberB * million * million = " << numberB * million * million << endl;실행 결과.
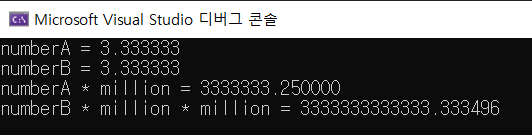
10.0 / 3.0 = 3.333333333(무한)이다. float형은 6번째 소수점까지는 잘 나타내지만, 그 이후에는 정확성이 떨어진다. double형은 15번째 소수점까지는 잘 나타내지만, 그 이후에는 정확성이 떨어진다. 따라서 float형은 6번째 double형은 15번째 소수점까지 유효하다고 할 수 있다.
각각의 자료형마다 부동 소수점을 저장하는 방식도 다르다. float형과 long double형은 부동 소수점수 뒤에 영문자를 붙여준다. 다음과 같이 저장한다.
8.57f // float형.
8.57F // float형.
8.57E8 // double형.
8.57 // double형.
8.67l // long double형.
8.29L // long double형.부동 소수점수의 단점으로는 정밀도가 떨어진다는 것이다. 다음 예제를 보자.
float a = 2.34e+22f;
float b = a + 1.0f;
cout << b - a << endl; //1이 나와야 마땅하다.실행 결과.

왜 이런 결과가 나왔을까? float형은 6번째 소수점까지밖에 못 나타내서, 22번째 숫자에 더하는 것은 아무 효과를 보지 못한다.
