자료구조 - Stack, Queue, Tree, Graph

seongmin·2022년 9월 24일

BFS DFS Graph Java queue stack tree

Java

목록 보기

15/30

Stack

Stack : 데이터(data)를 순서대로 쌓는 자료구조
Stack 의 특징은 입력과 출력이 하나의 방향으로 이루어지는 제한적 접근에 있다. 이런 Stack 자료구조의 정책을 LIFO(Last In First Out) 라고 부르기도 한다. Stack에 데이터를 넣는 것을 Push, 데이터를 꺼내는 것을 Pop 이라고 한다.
Stack 의 특징

1. LIFO(Last In First Out)
먼저 들어간 데이터가 제일 나중에 나오는 후입선출의 구조이다.

예1) 1, 2, 3, 4를 스택에 차례대로 넣는다.

Stack <Integer> stack = new Stack<>(); // Integer형 스택 선언

stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
---------------------------
1 <- 2 <- 3 <- 4
---------------------------
들어간 순서대로, 1번이 제일 먼저 들어가고 4번이 마지막으로 들어간다.

예2) 스택이 빌 때까지 데이터를 전부 빼낸다.

stack.pop();
stack.pop();
stack.pop();
stack.pop();
---------------------------

---------------------------
4, 3, 2, 1
제일 마지막에 있는 데이터부터 차례대로 나오게 된다.

2. 데이터는 하나씩 넣고 뺄 수 있다.
Stack 자료구조는 데이터가 아무리 많이 있어도 하나씩 데이터를 넣고 뺀다. 한꺼번에 여러 개를 넣거나 뺄 수 없다.

3. 하나의 입출력 방향을 가지고 있다.
Stack 자료구조는 데이터의 입출력 방향이 같다. 만약, 입출력 방향이 여러 개라면 Stack 자료구조라고 볼 수 없다.

실사용 예제 : 브라우저 앞으로가기, 뒤로가기 기능 구현

Queue

자료구조 Queue는 Stack과 반대되는 개념으로, 먼저 들어간 데이터(data)가 먼저 나오는 FIFO(First In First Out) 을 특징으로 가지고 있다. 입력과 출력의 방향이 고정되어 있으며, 두 곳으로 접근이 가능하다. Queue에 데이터를 넣는 것을 enqueue, 데이터를 꺼내는 것을 dequeue 라고 한다.
Queue 의 특징

1. FIFO (First In First Out)
먼저 들어간 데이터가 제일 처음에 나오는 선입선출의 구조를 가지고 있다.

예1) 1, 2, 3, 4를 큐에 차례대로 넣습니다.

Queue<Integer> queue = new LinkedList<>(); // int형 queue 선언

queue.add(1);     // queue에 값 1 추가
queue.add(2);     // queue에 값 2 추가
queue.add(3);     // queue에 값 3 추가
queue.add(4);     // queue에 값 4 추가

						   queue.add(데이터)
출력 방향 <---------------------------< 입력 방향
				     1 <- 2 <- 3 <- 4
				<---------------------------<
들어간 순서대로, 1번이 제일 먼저 들어가고 4번이 마지막으로 들어가게 된다.

예2) 큐가 빌 때까지 데이터를 전부 빼낸다.

queue.poll();       // queue에 첫번째 값을 반환하고 제거
queue.poll();
queue.poll();
queue.poll();

						   queue.poll()
출력 방향 <---------------------------< 입력 방향

				<---------------------------<
1, 2, 3, 4
제일 첫 번째 있는 데이터부터 차례대로 나오게 된다.

2. 데이터는 하나씩 넣고 뺄 수 있다.
Queue 자료구조는 데이터가 아무리 많이 있어도 하나씩 데이터를 넣고, 뺀다. 한꺼번에 여러 개를 넣거나 뺄 수 없다.

3. 두 개의 입출력 방향을 가지고 있다.
Queue 자료구조는 데이터의 입력, 출력 방향이 다르다. 만약 입출력 방향이 같다면 Queue 자료구조라고 볼 수 없다.

실사용 예제 : 프린터 출력 대기열

Tree

그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있다고 해서 트리 구조 라고 부른다.
트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클이 없다.

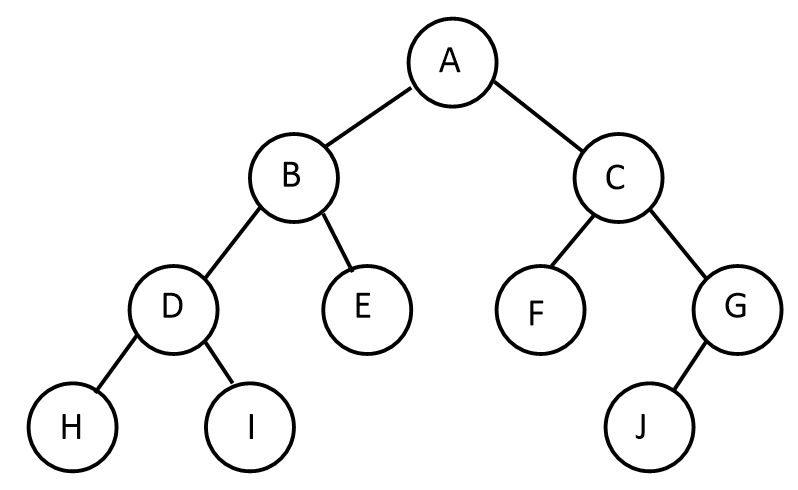
트리 구조는 루트(Root) (위 그림에서 A ) 라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge) 으로 연결한다. 각 데이터를 노드(Node) 라고 하며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계 를 가진다. 위 그림에서 A는 B와 C의 부모 노드(Parent Node) 이고, B와 C는 A의 자식 노드(Child Node) 이다. 자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드(Leaf Node) (위 그림에서 J ) 라고 부른다.
깊이 (depth)
트리 구조에서는 루트로부터 하위 계층의 특정 노드까지의 깊이(depth) 를 표현할 수 있다. 루트 노드는 지면에 있는 것처럼 깊이가 0이다. 위 그림에서 루트 A의 depth는 0이고, B와 C의 깊이는 1이다. D, E, F, G의 깊이는 2다.
레벨(Level)
트리 구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨(level) 로 표현할 수 있다. depth가 0 인 루트 A의 level은 1이다. depth가 1인 B와 C의 level은 2다. D, E, F, G의 레벨은 3이다. 같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node) 라고 한다.
높이(Height)
트리 구조에서 리프 노드를 기준으로 루트까지의 높이(height)를 표현할 수 있다. 리프 노드와 직간접적으로 연결된 노드의 높이를 표현하며, 부모 노드는 자식 노드의 가장 높은 height 값에 +1한 값을 높이로 가진다. 트리 구조의 높이를 표현할 때에는 각 리프 노드의 높이를 0으로 놓는다. 위 그림에서 H, I, E, F, J의 높이는 0이다. D와 G의 높이는 1이다. B와 C의 높이는 2다. 이때 B는 D의 height + 1 을, C는 G의 height + 1 을 높이로 가진다. 따라서, 루트 A의 높이는 3이다.
서브 트리(Sub tree)
트리 구조의 root 에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리 라고 부른다. (D, H, I)로 이루어진 작은 트리도 서브 트리이고, (B, D, E)나 (C, F, G, J)도 서브 트리다.
실사용 예제 : 파일 탐색기, 토너먼트 대진표, 가계도, 조직도 등

용어정리

노드(Node) : 트리 구조를 이루는 모든 개별 데이터
루트(Root) : 트리 구조의 시작점이 되는 노드
부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
리프(Leaf) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드

Graph

그래프는 여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조다.
자료구조의 그래프는 거미줄처럼 여러 개의 점들이 선으로 이어져 있는 복잡한 네트워크망과 같은 모습을 가지고 있다.

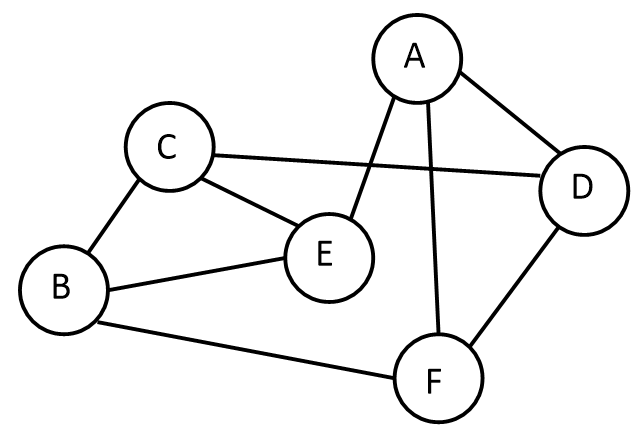
Graph 의 구조

직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있다.
간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(edge)이라고 한다.

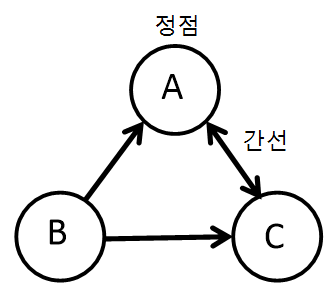
인접행렬

두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접하다고 말한다. 인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원 배열의 형태로 나타낸다. 만약 A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표다. 만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값을 저장한다.

[그림]그래프 예시

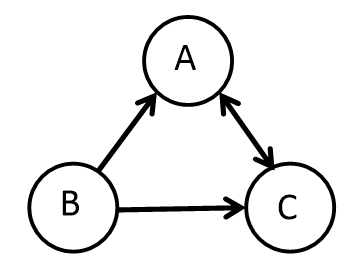
A의 진출차수는 1개 : A —> C
- [0][2] == 1
B의 진출차수는 2개 : B —> A, B —> C
- [1][0] == 1
- [1][2] == 1
C의 진출차수는 1개 : C —> A
- [2][0] == 1

인접행렬은 언제 사용하는가?

한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이하다.
- 예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0 번째 줄의 1 번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있다.
가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용된다.

인접 리스트

[그림] 내비게이션 그래프의 인접 리스트 예시

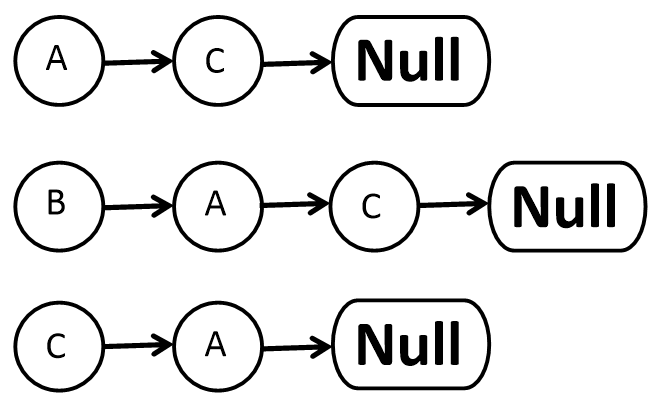
B는 A와 C로 이어지는 간선이 두 개가 있는데 ([그림]그래프 예시 참고), 왜 A가 C보다 먼저인가? 이 순서는 중요한가?

보통은 중요하지 않다. 그래프, 트리, 스택, 큐 등 모든 자료구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제할 수 있다. 그래프를 인접 리스트로 구현할 때, 정점별로 살펴봐야 할 우선 순위를 고려해 구현할 수 있다. 이때, 리스트에 담겨진 정점들을 우선 순위별로 정렬할 수 있다. 우선 순위가 없다면, 연결된 정점들을 단순하게 나열한 리스트가 된다.

우선 순위를 다뤄야 한다면 더 적합한 자료구조(ex. queue, heap)를 사용하는 것이 합리적입니다. 따라서 보통은 중요하지 않습니다. (언제나 예외는 존재한다.)

인접 리스트는 언제 사용할까?

메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용한다.
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.

그래프 용어들

정점 (vertex): 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소다.
간선 (edge): 정점 간의 관계를 나타낸다. (정점을 이어주는 선)
인접 정점 (adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 의미한다.
가중치 그래프 (weighted Graph): 연결의 강도(추가적인 정보, 위의 예시에서는 서울-부산으로 가는 거리 등)가 얼마나 되는지 적혀져 있는 그래프를 의미한다.
비가중치 그래프 (unweighted Graph): 연결의 강도가 적혀져 있지 않는 그래프를 의미한다.
무(방)향 그래프 (undirected graph) : 앞서 보았던 내비게이션 예제는 무(방)향 그래프다. 서울에서 부산으로 갈 수 있듯, 반대로 부산에서 서울로 가는 것도 가능하다. 하지만 단방향(directed) 그래프로 구현된다면 서울에서 부산을 갈 수 있지만, 부산에서 서울로 가는 것은 불가능하다(혹은 그 반대). 만약 두 지점이 일방통행 도로로 이어져 있다면 단방향인 간선으로 표현할 수 있다.
진입차수 (in-degree) / 진출차수 (out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타낸다.
인접 (adjacency) : 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점이다.
자기 루프 (self loop) : 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다. 다른 정점을 거치지 않는다는 것이 특징이다.
사이클 (cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다. 내비게이션 그래프는 서울 —> 대전 —> 부산 —> 서울 로 이동이 가능하므로, 사이클이 존재하는 그래프다.

Binary Search Tree

이진 트리(Binary tree)는 자식 노드가 최대 두 개인 노드들로 구성된 트리다. 이 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있다.
이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉜다.

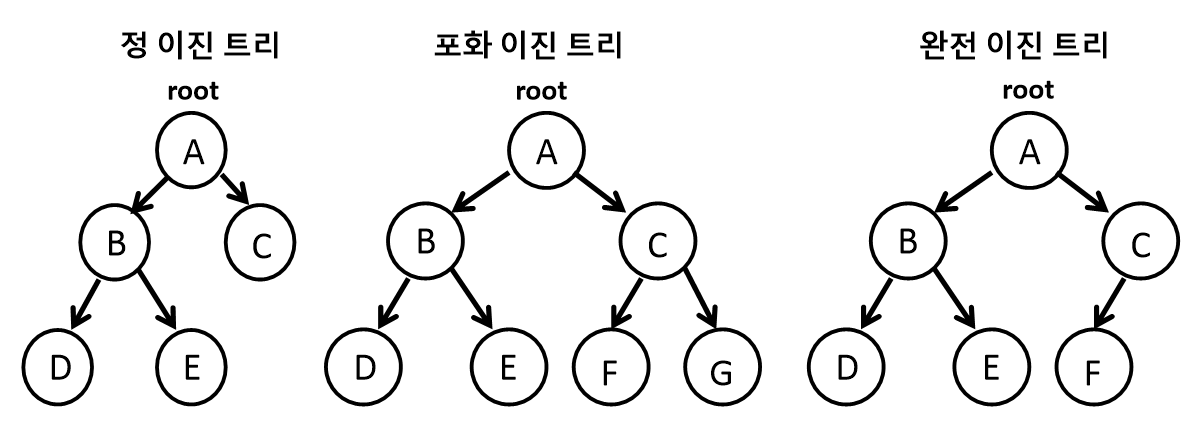
정 이진 트리(Full binary tree) : 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
포화 이진 트리(Perfect binary tree) : 정 이진 트리이면서 완전 이진 트리인 경우다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리다.
완전 이진 트리(Complete binary tree) : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 한다.

이진 탐색 트리(Binary Search Tree) 는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다.

이진 탐색 트리는 균형 잡힌 트리가 아닐 때, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있다. 균형이 잡히지 않은 트리는 탐색하는 데 시간이 더 걸리는 경우도 있기 때문에 해결해야 할 문제인데, 이 문제를 해결하기 위해 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가할 수 있다.

순회방법

Inorder : Left -> Root -> Right 순으로 순회

D - B - E - A - C 순서
Preorder : Root -> Left -> Right 순으로 순회

A - B - D - E - C 순서
Postorder : Left -> Right -> Root 순으로 순회

D - E - B - C - A 순서

		 (1)
       ↙    ↘
      (2)     (3)
   ↙    ↘
  (4)    (5)
     
//Inorder (Left, Root, Right) : 4 2 5 1 3
//Preorder (Root, Left, Right) : 1 2 4 5 3
//Postorder (Left, Right, Root) : 4 5 2 3 1

class Node {
int data;
Node left;
Node right;
}

class Tree {
	public Node root;
    
    public void setRoot(Node node) {
    	this.root = node;
        }
        public Node getRoot() {
        return root;
        }
        public Node makeNode(Node left, int data, Node right) {
        Node node = new Node();
        node.data = data;
        node.left = left;
        node.right = right;
        return node;
     }
     public void inorder(Node node) {
       if (node != null) { // node가 null이 아닐 때 까지 재귀호출 반복
       inorder(node.left); // left
       System.out.println(node.data);  // root
       inorder(node.right); // right
       }
    }
     public void preorder(Node node) {
     if (node != null) {
     System.out.println(node.data); // root
     preorder(node.left); // left
     preorder(node.right); // right
     }
 }
 	 public void postorder(Node node) {
     if (node != null) {
     postorder(node.left); // left
     postorder(node.right); // right
     System.out.println(node.data); // root
     }
   }
 }  
 		 (1)
       ↙    ↘
      (2)     (3)
   ↙    ↘
  (4)    (5)
     
//Inorder (Left, Root, Right) : 4 2 5 1 3
//Preorder (Root, Left, Right) : 1 2 4 5 3
//Postorder (Left, Right, Root) : 4 5 2 3 1
public class Test {
public static void main (String[] args) {
	Tree t = new Tree();
    Node n4 = t.makeNode(null, 4, null);
    Node n5 = t.makeNode(null, 5, null);
    Node n2 = t.makeNode(n4, 2, n5);
    Node n3 = t.makeNode(null, 3, null);
    Node n1 = t.makeNode(n2, 1, n3);
    t.setRoot(n1);
    t.inorder(t.getRoot()); 
    
*/출력값
4
2
5
1
3
    Node n4 = t.makeNode(null, 4, null);
    Node n5 = t.makeNode(null, 5, null);
    Node n2 = t.makeNode(n4, 2, n5);
    Node n3 = t.makeNode(null, 3, null);
    Node n1 = t.makeNode(n2, 1, n3);
    t.setRoot(n1);
    t.preorder(t.getRoot()); 
    
*/출력값
1
2
4
5
3
    Node n4 = t.makeNode(null, 4, null);
    Node n5 = t.makeNode(null, 5, null);
    Node n2 = t.makeNode(n4, 2, n5);
    Node n3 = t.makeNode(null, 3, null);
    Node n1 = t.makeNode(n2, 1, n3);
    t.setRoot(n1);
    t.postorder(t.getRoot()); 
    
*/출력값
4
5
2
3
1

BFS(Breadth-First Search)

너비를 우선적으로 탐색하는 방법을 Breadth-First Search, 너비 우선 탐색 이라고 한다. 주로 두 정점 사이의 최단 경로를 찾을 때 사용한다. 만약, 경로를 하나씩 전부 방문한다면, 최악의 경우에는 모든 경로를 다 살펴보아야 하는 케이스도 존재한다.
Queue를 이용해서 구현

Queue를 먼저 만드는데 아무것도 없으니 먼저 시작 노드를 넣음 (0부터 시작하지 않아도 된다)
Queue 에서 하나 추출하고 그 추출한 노드의 인접한 노드들을 큐에 추가
들어간 적이 있던 인접한 노드들은 제외하고 큐에 추가
이러한 과정을 반복하며 큐에 있는 노드들을 추출할 때 추가할 인접한 노드가 없다면 추출만하고 다음으로 이동

DFS(Depth-First Search)

DFS는 하나의 경로를 끝까지 탐색한 후, 찾고자 하는 정점이 아니라면 다음 경로로 넘어가 탐색한다. 하나의 경로를 끝까지 들어가서 확인하고 다음으로 넘어가기 때문에, 운이 좋다면 단 몇 번 만에 경로를 찾을 수도 있다. 또 정점을 찾는 길이 아님을 미리 체크할 수 있다면, 바로 그 순간 다음 탐색으로 넘어갈 수 있다. 깊이를 우선적으로 탐색하는 방법을 Depth-First Search, 깊이 우선 탐색 이라고 한다.
Stack을 이용해서 구현