[Java] 진법

참고
자바의 정석

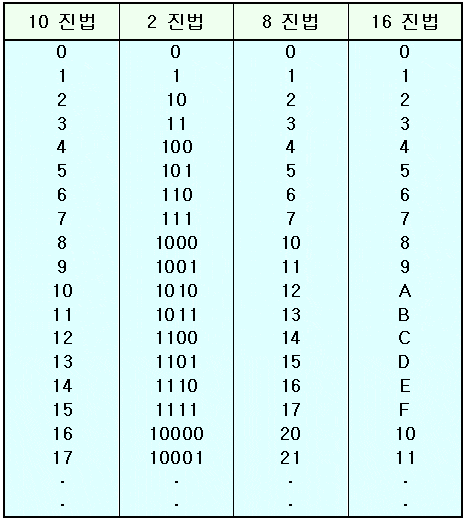
10진법과 2진법

• 우리는 일상생활에서 흔히 10진법을 사용한다. 아마 손가락이 10개여서
  우리 인간은 10진법을 받아들였던것 같다.
• 이처럼, 애니악이라는 컴퓨터에도 10진법을 적용시켜보았지만 전압이
  매우 불안정했다. 그래서 컴퓨터 같은 기계에는 전기가 흐르면 1, 전기가
  흐릐지 않으면 0인 2진법을 도입시키게 되었다.
• 그래서 2진법을 제대로 알지 못하면, 컴퓨터의 동작원리, 데이터 처리방식을
  온전히 이해할 수 없게 된다.
• 변수의 저장원리도 마찬가지다. 지금까지는 10진수가 저장되는 것처럼 설명을
  했지만, 사실은 10진수의 정수가 대입이되면, 10진수의 정수가 2진수로 변환되어 저장이 된다.
• 2진법은 0과 1로만 데이터를 표현하기 때문에, 10진수보다 많은 자릿수가
  필요하다.
• 2진수가 자릿수가 많이 필요하긴 하지만, 10진수를 온전히 표현 못하는건 아니다.
  덧셈이나 뺄쎔같은 연산도 10진수와 동일한 로직이다.

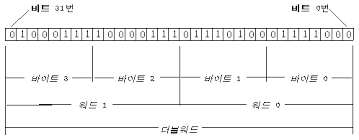
비트와 바이트

• 한 자리의 2진수를 비트라고 하며, 1비트는 컴퓨터가 값을 저장할 수 있는
  최소단위이다.
• 8비트를 1바이트라고 하며, 데이터의 기본단위로 사용한다.
• 워드는 CPU가 한번에 처리할 수 있는 데이터의 크기를 말하며,
  워드의 크기는 4바이트이긴 하지만 CPU성능에 따라 달라진다.
  ex). 32비트 CPU에서는 1워드는 4바이트이고 64비트 CPU에서는 1워드는 8바이트이다.

참고
nibble: 4bit, 16진수 1자리 (2진수 4자리)를 저장할 수 있는 단위

n비트로 표현할 수 있는 10진수

• 값의 개수 : 2^n
• 값의 범위 : 0 ~ (2^n)-1

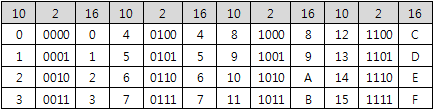
8진법과 16진법

• 8진수는 2진수 3자리를, 16진수는 2진수 4자리를 각각 한자리로 표현할 수 있기 때문에 자리수가 짧아져서 알아보기 쉽고 서로간의 변환방법 또한 매우 간단하다.

2진수를 8진수, 16진수로 변환

정수의 진법 변환

• 10진수를 n진수로 변환
  • 10진수를 다른 진수로 변환할려면 해당 진수로 나누고
    나머지 값을 옆에 적는 것을 더 이상 나눌 수 없을 때까지
    반복한 다음 마지막 몫과 나머지를 아래부터 위로 순서대로 적으면 된다.
• n진수를 10진수로 변환
  • 어떤 진법의 수라도 변환하는 방법은 똑같다. 각 자리의 수에 해당
    단위의 값을 곱해서 더하면 된다.

실수의 진법 변환

• 10진 소수점수를 2진 소수점수로 변환하는 방법

  • 10진 소수점수를 2진 소수점수로 변환하는 방법은 10진 소수점수에
    2를 계속 곱하는 것이다.

    ex) 0.625의 십진수를 2진수로 변화할려면?
    1) 10진 소수에 2를 곱한다.
    2) 위의 결과에서 소수부만 가져다가 2를 곱한다.
    3) 1,2의 과정을 소수부가 0이 될때 까지 반복한다.
    4) 위의 결과에서 정수부만을 위에서 아래로 순서대로 적고 '0.'을 앞에 붙인다.

• 2진 소수점수를 10진 소수점수로 변환하는 방법
  • 소수점수를 가져다가 (2^-n)식으로 곱해주면 된다.

음수의 2진 표현 - 2의 보수법

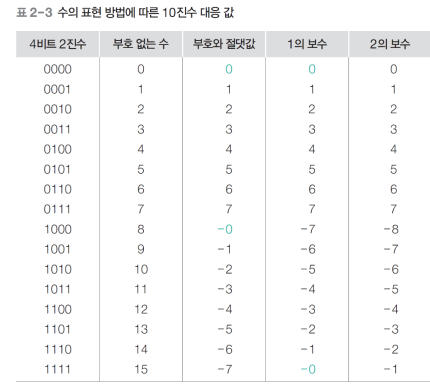
• 우리가 앞에서 살펴봤듯이 n비트의 2진수로 표현할 수 있는 부호없는 정수의 값의 개수는 2^n이다.
• 그러면 양수와 음수를 둘다 표현할려면 어떻게 해야할까?
• 왼쪽의 첫번째 비트 (MSB)가 0이면 양수, 1이면 음수로 첫번째 비트만으로
  값의 부호를 알 수 있다.
• 하지만, 첫번째 비트만 바꿔주면 문제점이 발생한다. 양수의 2진수로 첫번째 비트를 1로만 바꿔준 음수를 더하면 논리상 0이되어야 하지만 그렇지가 않는다.
  또한, 0과 -0이 2개가 생긴다는 단점이 있다. 게다가 2진수가 증가할때 10진수는 감소한다는 단점이 존재한다.
• 하지만 2의 보수법을 이용하면 위의 문제점들이 해결이 가능하다. 다만, 첫번째 비트만 바꿔서 음수가 된다는 장점은 사라진다. 하지만 내 생각이지만, 수 많은 단점을 해결하고 장점을 포기한다는 것은 당연한 해결이라고 생각한다.

2의 보수법

• 어떤수의 'n의 보수'는 더했을 때 n이 되는 수를 말한다.
• 2의 보수도 마찬가지로 더해서 2가되는 두수의 관계를 말한다.
• 즉, 10진수 2는 2진수로 '10'을 의미하며, 자리올림이 발생하고 0이 되는 수를 2의 보수라고 볼수 있다.
• 그래서, 2의 보수 관계를 지닌 두 2진수를 더하면, (자리올림이 발생하고) 0이된다.
• 그래서 2의 보수를 어떻게 구해야 할까? 정답은 각 자리의 수가 1이면 0으로 0이면 1로 바꾼 수에서 1을 덧셈연산을 한다.
• 그러면 음수를 2진수로 바로 변환은 가능할까? 물론 가능하다.
  • 10진 음의 정수를 절대값을 2진수로 변환하고, 2의 보수를 구하면 된다.

음수의 2진 표현을 구하는 방법
1. 음수의 절대값을 2진수로 변환한다.
: -5의 절대값인 5를 2진수로 변환한다. 10진수 5를 2진수로 변환하면 '0101'이 된다.
2. 위의 결과에서 1를 0으로 0을 1로 바꾼다. (1의 보수 구하기)
: '0101'이 '1010'이 된다.
3. 위의 결과에서 1을 더한다. (2의 보수 구하기, 1의 보수 + 1)
: '1010'에 1을 더하면 '1011'이 되고 이것이 -5의 2진표현이다.