[Baekjoon] 13144 List of Unique Number (C++)

문제 링크

BOJ_13144: List of Unique NUmber

문제

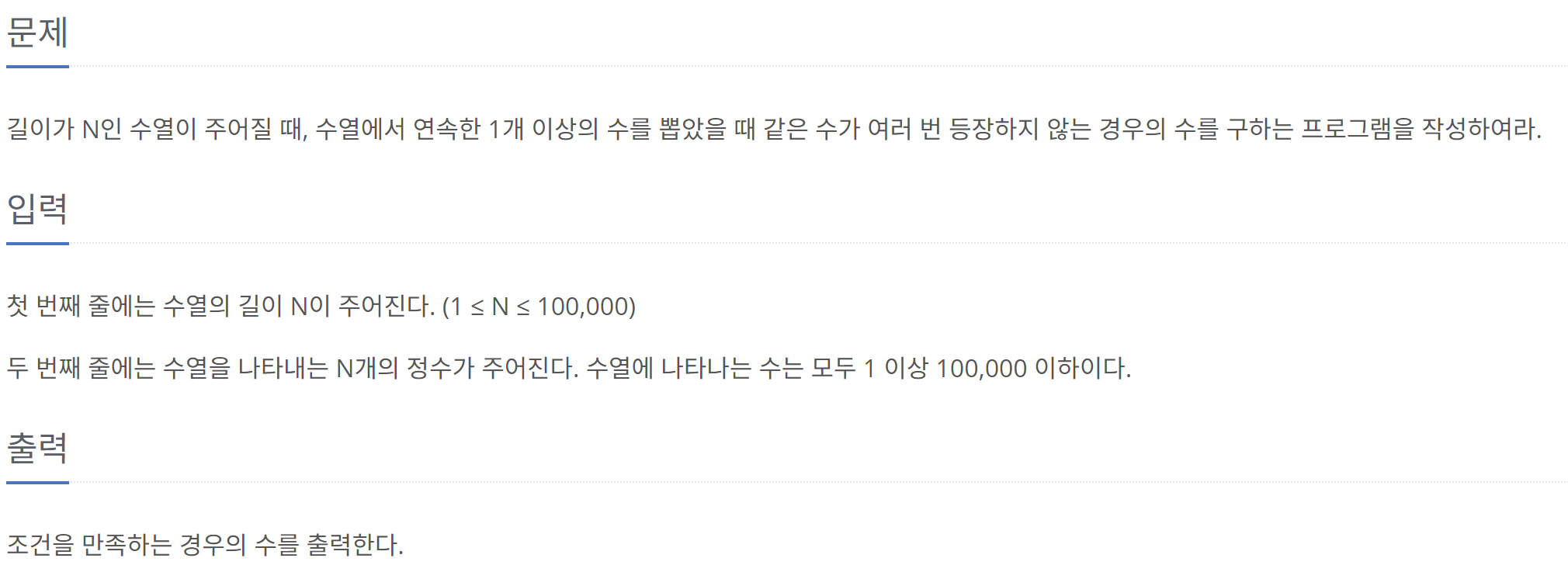
길이가 N인 수열에서 연속한 부분 수열 중 같은 수가 여러번 등장하지 않는 경우의 수를 세는 문제이다.

풀이

길이가 M이면서 각각의 요소가 중복되지 않는 부분수열이 있다고 가정했을 때, 해당 부분수열에서 나오는 모든 부분수열은 원소가 중복되지 않는다.

즉 길이가 총 M개의 서로다른 원소를 가진 수열이 있다면, 조건을 만족하는 경우의 수는 (M+1)*M/2가 된다.
ex) {1, 2, 3} -> 6개
{1}, {2}, {3}, {1, 2}, {2, 3}, {1, 2, 3}

이 규칙성을 찾았다면 주어진 길이 N 수열에서 조건을 만족하는 연속된 최대 길이의 부분수열을 찾은 후 위의 공식으로 계산해주면 된다.

s, e 로 인덱스를 조절하면서 s와 e사이에 있는 수에 대한 정보를 cnt배열에 저장한다.
e를 계속 증가시키며 최대한 넓은 구간이 되도록 한다.
그 과정에서 두가지 경우가 존재한다.

• 1. e에 해당하는 수가 현재 s와e사이 구간에 존재하지 않는 경우
  • cnt에 해당 수가 이제 구간 안에 존재함을 표시하고 e를 증가시킨다.

• 2. e에 해당하는 수가 현재 s와e사이 구간에 존재하는 경우.
  • 2-1. s와 e-1 사이는 각 요소가 서로 다르므로 해당 구간에서 가능한 부분수열의 개수를 계산한다.
  • 2-2.s를 e에 해당하는 수가 존재하지 않을 때까지 증가시켜서 구간을 업데이트 한다.
  • 2-3. 중복 계산되는 증가된s와 e사이에서 가능한 부분수열의 개수를 빼준다. (e가 수열의 마지막에 도달했을 경우 제외)

주의할 점

가능한 최대 경우의 수는 100001 * 100000 / 2 이므로 int의 범위를 넘어간다.

중복으로 개수를 세는 경우가 발생하므로 2-3 작업을 해주어야 한다.

코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>

#define endl "\n"

using namespace std;

int N;
int arr[101010];
int cnt[101010];

void Solve() {
    int s, e;
    long long answer = 0;
    cin>>N;
    for(int i=1; i<=N; i++){
        cin>>arr[i];
    }

    s= e = 1;
    while(e<=N+1){
        if(cnt[arr[e]] == 0 && e != N+1){
            cnt[arr[e]]++;
        }
        else{
            answer+= (double)(e-s + 1)*(e-s)/2;
            while(cnt[arr[e]]!=0 && s<e) cnt[arr[s++]]--;
            cnt[arr[e]]++;
            if(e!=N+1) answer-= (double)(e-s + 1)*(e-s)/2;
        }
        e++;
    }

    cout<<answer;
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    Solve();

    return 0;
}