[Baekjoon] 2283 구간 자르기 (C++)

문제 링크

BOJ 2283: 구간 자르기

문제

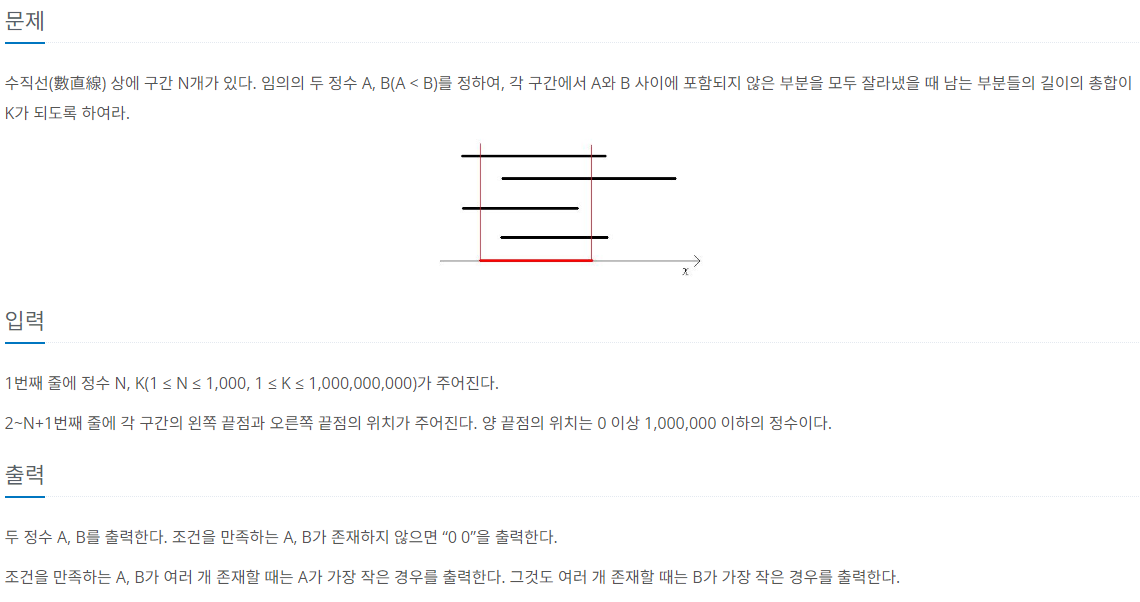
문제가 간단하고 명확히 이해가 돼서 좋은 문제였다.

• 특정 구간 안에 포함된 수직선 길이의 합이 K가 되도록 하는 구간을 구하는 문제이다.

• 구간이 여러개일 경우에는 시작점이 가장 작은 경우, 그 다음으로는 끝 점이 가장 작은 경우를 우선으로 하여 결과를도출한다.

풀이

각 지점마다 포함하는 길이에 대한 정보를 가진다면 쉽게 해결할 수 있을 것 같았다.

st배열과 ed배열을 이용해서 각 지점에서 시작되는 수직선과 끝나는 수직선의 개수를 저장한다.

그 다음으로 st와 ed를 이용해 i번째 지점에 존재하는 수직선의 개수를 구할 수 있다.

i번째 이전에 시작된 수직선의 개수 합 - i번째 이전에 시작됐다가 끝난 수직선의 개수 합 = i번째에 존재하는 수직선의개수

for(int i=0; i<=1000000; i++){
        tmp+=st[i]; tmp -= ed[i];
        arr[i] = tmp;
    }

이렇게 정보를 구성했다면 투포인터를 이용해 문제를 해결한다.
arr배열의 값을 이용하여 s와e사이에 포함되는 수직선 길이의 합을 구할 수 있다. 구간을 조절해가면서 합이 K가 되는 경우를 찾는다.

코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>

#define endl "\n"
#define MAX_LOC 1000000
using namespace std;

int N, K;
int st[1010101];
int ed[1010101];
int arr[1010101];

void Solve() {
    cin>>N>>K;
    int a, b, tmp, nowLen, s, e;

    for(int i=0; i<N; i++){
        cin>>a>>b;
        st[a]++; ed[b]++;
    }

    tmp = 0;
    for(int i=0; i<=1000000; i++){
        tmp+=st[i]; tmp -= ed[i];
        arr[i] = tmp;
    }

    nowLen = s = e = 0;
    for(s=0; s<MAX_LOC; s++){
        while(nowLen < K && e < MAX_LOC){
            nowLen+=arr[e]; e++;
        }
        if(nowLen==K) break;
        nowLen-=arr[s];
    }
    if(nowLen!= K) cout<<"0 0";
    else cout<<s<<" "<<e;
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    Solve();

    return 0;
}