Logistic Regression as a NN
-
Binary Classification
Input : Cat image[RGB] 64x64x3 = 12288 x 1
Output : 1(cat) vs 0(non cat) -
Logistic Regression
x : input
y : output
y hat : Probability of y , P(y=1|x)
parameters : w - x dimension vector , b - real number
y hat = @(w.T × x + b) (@ : sigmoid) = a
Z = w.T × x + b
@ = 1/(1+e^-z) -
Cost Function :
Loss Function L(a, y)
= -{ylog(a) + (1-y)log(1-a)}
Cost Function J(w,b)
= 1/m * {∑ L(y hat, y)} -
Gradient Descent(경사 하강)
목표 : To find w,b that minimize J(w,b)
w: = w - α {dJ(w,b)/dw}
b: = b - α {dJ(w,b)/db}
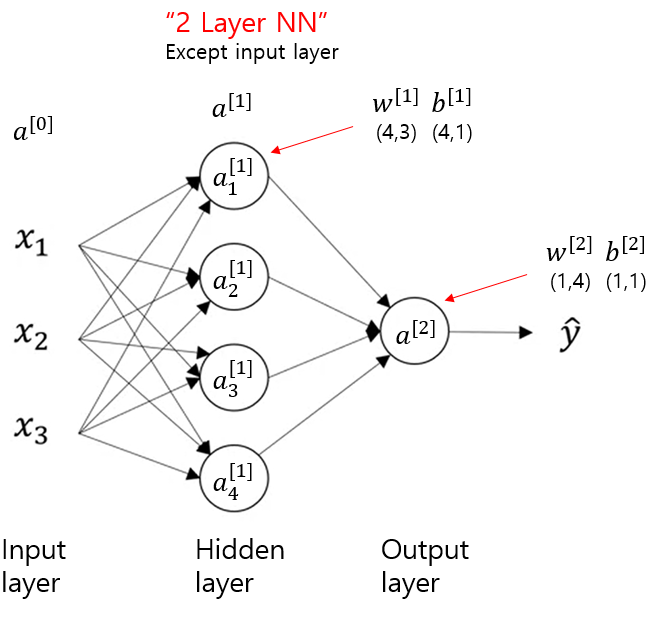
Neural Network
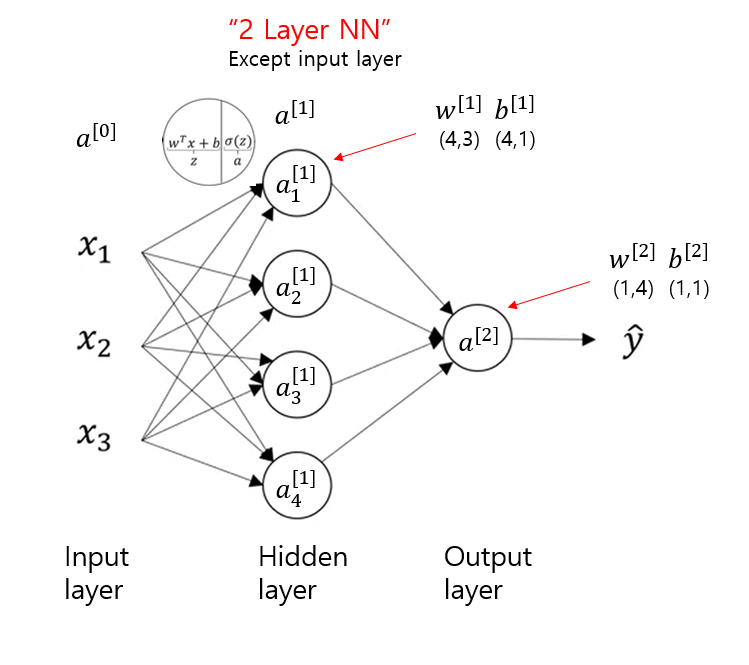
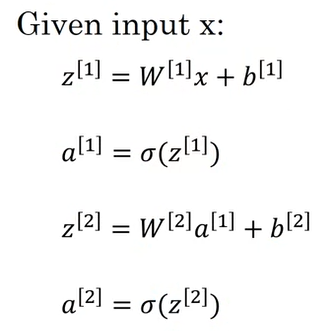
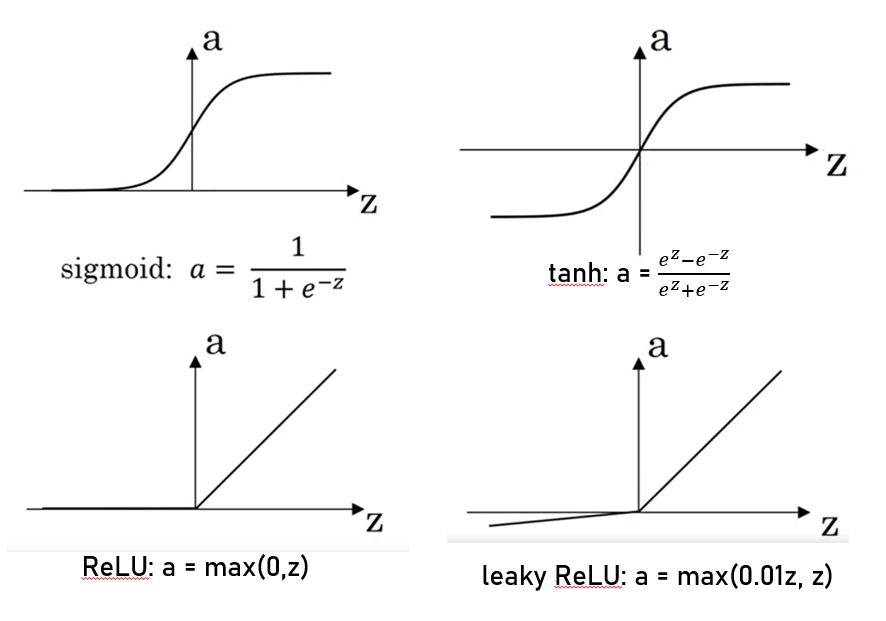
Activation Function
Gradient Descent
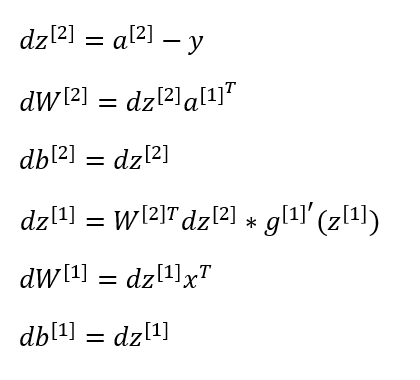
Defining the nn structure
2-layer NN
1. layer_sizes
n_x : input layer
n_h : hidden layer 주로 4
n_y : output layer
2. initialize the model's parameters
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
3. forward propagation
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
4. compute_cost : compute the J (cross-entropy cost)
logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
cost = - np.sum(logprobs) / m
5. Back propagation
dZ2 = A2 - Y
dW2 = (1/m) * np.dot(dZ2,A1.T)
db2 = (1/m) * np.sum(dZ2,axis=1, keepdims = True)
dZ1 = np.multiply(np.dot(W2.T,dZ2), 1-np.power(A1,2))
dW1 = (1/m) * np.dot(dZ1,X.T)
db1 = (1/m) * np.sum(dZ1,axis=1,keepdims = True)
6. update_parameters
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
7. nn_model
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x, n_h, n_y)
for i in range(0, num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2, Y)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters, grads)
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
8. predict
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2)
** hidden layer tuning **
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size)*100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))Multi-layer NN
1. initialize_parameters
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h,1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y,1))
2. initialize_params_deep
L = len(layer_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
3. linear_forward
Z = np.dot(W,A) + b
4. linear_activation_forward
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
cache = (linear_cache, activation_cache)
5. L-model_forward
caches = []
A = X
L = len(parameters) // 2
for l in range(1, L):
A_prev = A
#(≈ 2 lines of code)
# A, cache = ...
# caches ...
# YOUR CODE STARTS HERE
A, cache = linear_activation_forward(A_prev,
parameters['W' + str(l)],
parameters['b' + str(l)],
activation='relu')
caches.append(cache)
AL, cache = linear_activation_forward(A,
parameters['W' + str(L)],
parameters['b' + str(L)],
activation='sigmoid')
caches.append(cache)
6. compute_cost
m = Y.shape[1]
cost = (-1/m) * np.sum(np.multiply(Y,np.log(AL))+ np.multiply(1-Y,np.log(1-AL)))
cost = np.squeeze(cost)
7. linear backward
A_prev, W, b = cache
m = A_prev.shape[1]
dW = (1/m) * np.dot(dZ, A_prev.T)
db = (1/m) * np.squeeze(np.sum(dZ, axis=1, keepdims=True))
dA_prev = np.dot(W.T, dZ)
8. linear activation backward
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
9. L-model backward
grads = {}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
current_cache = caches[L-1]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL, current_cache, 'sigmoid')
grads["dA" + str(L - 1)] = dA_prev_temp
grads["dW" + str(L)] = dW_temp
grads["db" + str(L)] = db_temp
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l+1)], current_cache, 'relu')
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
10. update_parameters
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads['dW'+str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads['db'+str(l+1)] 