[Deeplearning Andrew Ng강의_2] : Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization #1

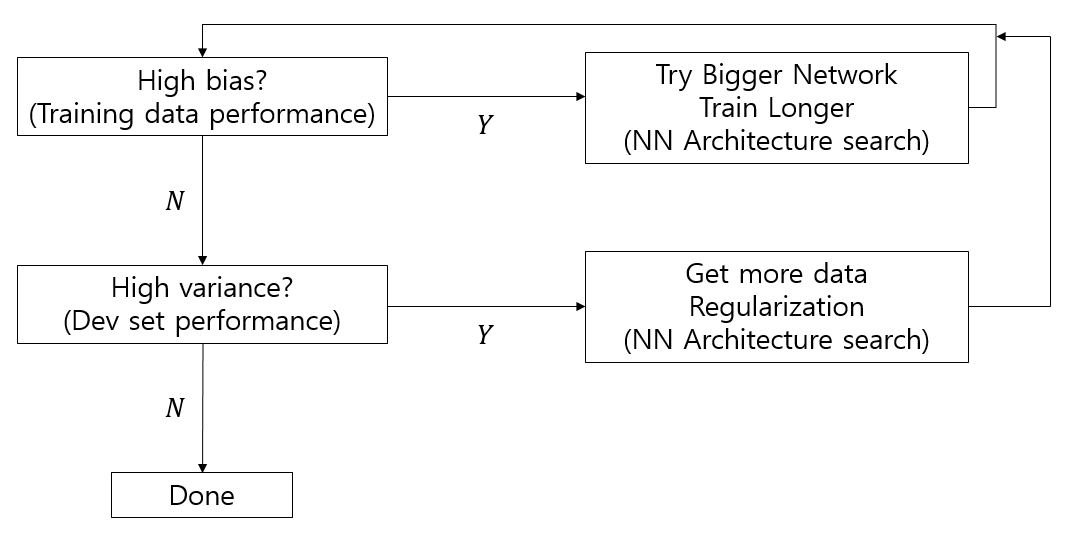
Basic Recipe for ML

Regularization

Overfitting --> high variance --> No more Data --> Regularization!!

Logistic Regression

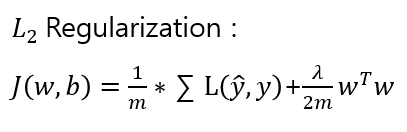Euclidean norm / 뒤에 b 정규화는 생략-->영향을 주지 않음
L1 Regularization 도 존재하지만 L2를 더 유용하게 씀.

Neural Network

"Frobenius norm"

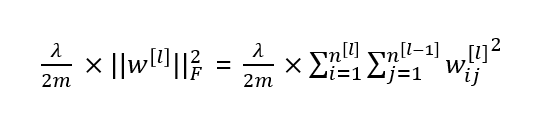
Why does Regularization help with overfitting?

𝜆(Reg.param.)가 커지면 w가 0에 가깝게 작아진다. 그러면 Z도 0에 가까워진다.
tanh 함수 기준으로 z가 0에 가까워지면 직선의 형태(Linear)를 띠게 되는데 이 때 거의 간단한 Logistic Regression 을 하는 것처럼 된다. 결국 가중치가 감쇠되는 효과이다.
주의
Regularization 과 Normalization 은 서로 다른 것!! 똑같이 정규화라고 해석되어 혼동할 수 있다.

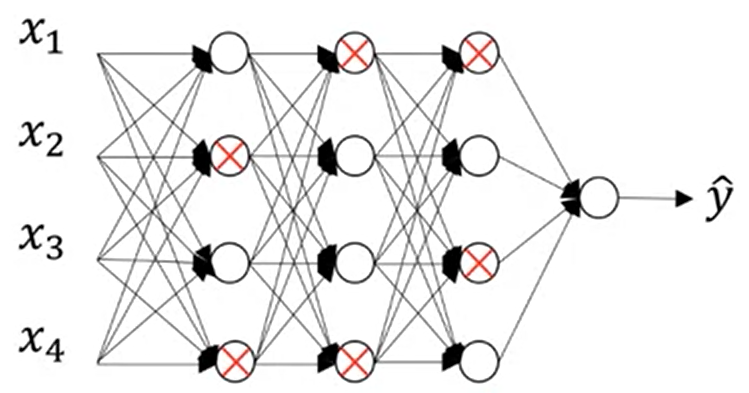
Dropout regularization

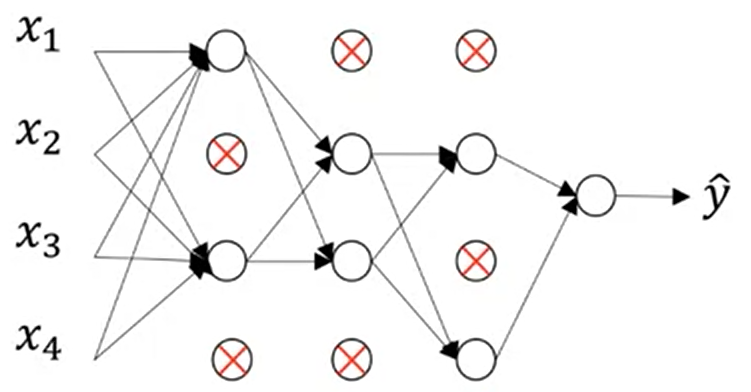
Overfitting 이 된 경우, 이를 해결하기 'Dropout'을 적용
위와 같은 경우 0.5의 확률로 각 hidden layer 노드를 제외시킨다. 이 후 역전파를 진행시키면 작은 네트워크가 학습되면서 overfitting을 감소 시킬 수 있다.

과정 : Linear -> RELU + Dropout -> Linear -> RELU + Dropout -> Linear -> RELU + Dropout -> Linear -> Sigmoid.

Inverted Dropout

keep_prob - probability of keeping a neuron active during drop-out
if keep_prob = 0.8 : 각 층마다 80% 확률로 뉴런을 유지하고, 20% 확률로 뉴런을 제거
활성화함수 이 후 꼭 keep_prob으로 나눠 줘야하는데 이는 최초 데이터 크기를 유지해야하기 때문이다. 또한 순전파에서 Dropout을 했다면 역전파에서도 Dropout을 해야한다.

Other methods

• Data Augmentation
• Early stopping

Optimization

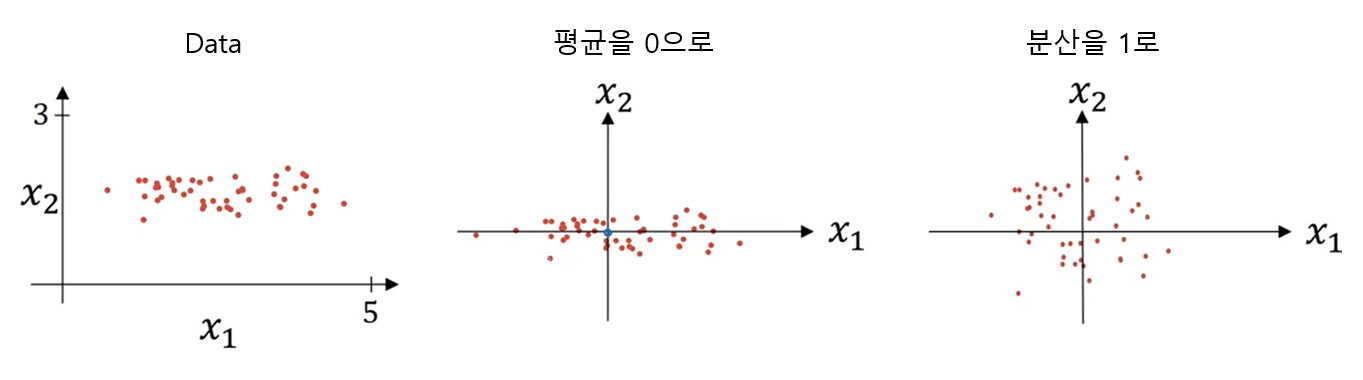
Normalizing inputs

Weight Initialization

기울기 하강시 문제가 될 수 있는 부분 :
Vanishing gradients - 기울기가 너무 작아져서 weight 변화가 없는 경우
Exploding gradients - 기울기가 너무 커져서 weight 변화가 너무 큰 경우
해결하는 방법 : 가중치 초기화
w[l] = np.random.randn("shape") * np.sqrt(1 / n[l-1])
-> tanh일 때 1 (Xavier initialization)
-> RELU일 때는 1 대신 2

Debug

Gradient Checking - 내가 한 역전파가 옳은가?

1. 모든 W, b matrix를 벡터로 변경 -> big vector θ
2. 모든 dw, db matrix를 벡터로 변경 -> big vector dθ
3. dθapprox = dθ 같은지 확인
   dθapprox = {J(θ1,θ2,...θi+ε) - J(θ1,θ2,...θi-ε)} / 2ε
4. Check : 유클리드 거리 공식 이용 --> ε이 거의 10^-7이면 great! / ε이 거의 10^-3이면 Worry!