✅ 오늘 한 일
- Project BCA
📝 배운 것들
🏷️ Unity : transform 좌표계 기준
기본적으로 transform.position과 transform.rotation은 월드 좌표계 (World Space) 기준이야.
즉, 어떤 오브젝트가 다른 오브젝트(부모)의 자식으로 있어도, transform.position을 가져오면 월드 좌표 기준의 위치를 반환하고, transform.rotation도 월드 좌표 기준의 회전값(쿼터니언) 을 반환해.
만약 로컬 좌표(Local Space) 기준으로 값을 가져오고 싶다면,
transform.localPosition→ 부모 기준의 위치transform.localRotation→ 부모 기준의 회전
을 사용하면 돼.
🏷️ Unity : 두 벡터 사이의 각도 구하기
1. 특정 축을 기준으로 방향 벡터의 각도(Angle) 구하기
유니티에서 벡터 간의 각도를 구하는 가장 쉬운 방법은 Vector3.Angle() 을 사용하는 거야.
✅ 두 벡터 사이의 각도 구하기
Vector3 worldDirection = new Vector3(1, 0, 1); // 예제 방향 벡터
Vector3 referenceDirection = Vector3.forward; // 기준 (월드 기준 앞 방향)
float angle = Vector3.Angle(referenceDirection, worldDirection);
Debug.Log("각도: " + angle);👉 Vector3.Angle() 은 두 벡터 사이의 최소한의 각도(0~180도) 를 반환해.
2. 2D 또는 특정 축을 기준으로 회전 방향(시계방향 / 반시계방향) 포함한 각도 구하기
Vector3.Angle()은 항상 절대적인 각도(0~180도)만 반환하기 때문에, 회전 방향을 포함하려면 외적 (cross product) 을 활용해야 해.
✅ 특정 축을 기준으로 방향 벡터의 Signed Angle(부호 있는 각도) 구하기
Vector3 worldDirection = new Vector3(1, 0, 1); // 예제 방향 벡터
Vector3 referenceDirection = Vector3.forward; // 기준 (월드 앞 방향)
Vector3 upVector = Vector3.up; // Y축 기준으로 좌우 회전 각도 구하기
float signedAngle = Vector3.SignedAngle(referenceDirection, worldDirection, upVector);
Debug.Log("부호 있는 각도: " + signedAngle);👉 Vector3.SignedAngle() 은 부호를 포함한 각도(-180 ~ 180도) 를 반환해.
signedAngle > 0👉 반시계방향(왼쪽 회전)signedAngle < 0👉 시계방향(오른쪽 회전)
3. 특정 오브젝트의 방향을 월드 좌표 기준으로 구하기
어떤 오브젝트가 바라보는 방향(transform.forward)이 월드 좌표에서 몇 도인지 알고 싶다면?
float angle = Vector3.SignedAngle(Vector3.forward, transform.forward, Vector3.up);
Debug.Log("오브젝트가 월드 앞방향(Vector3.forward) 기준 몇 도 회전했는지: " + angle);👉 Vector3.forward를 기준으로, transform.forward가 얼마나 회전했는지 Y축을 기준으로 구함
👉 ex) 90도면 오른쪽(+X) 방향, -90도면 왼쪽(-X) 방향
🎮 Project BCA
FEN 기보 체스판으로 보여주는 사이트 : http://www.ee.unb.ca/cgi-bin/tervo/fen.pl
체크메이트 로직 추가

3회 동형은 구현 난이도에 비해 실용성이 없어서 패스
public void EnterState()
{
Debug.Log("Entering Black Turn");
moveValidator.ResetAllPieceMoves(); // 캐싱했던 데이터를 전부 리셋하고
moveValidator.CalculateMyMoves(gameManager.whiteTurn); // 미리 경로를 전부 계산해놓는다
if (board.GetHalfMoveCount() >= 50)
{
Debug.Log("50수 룰로 인한 패배");
}50수 룰은 패배 처리함
로봇 팔 IK 로직 구현
모델 키우기

씬에 갖다놓고 테스트 해봤는데 아직도 짧음
저번엔 원근법 때문에 닿는 줄 알았던 거
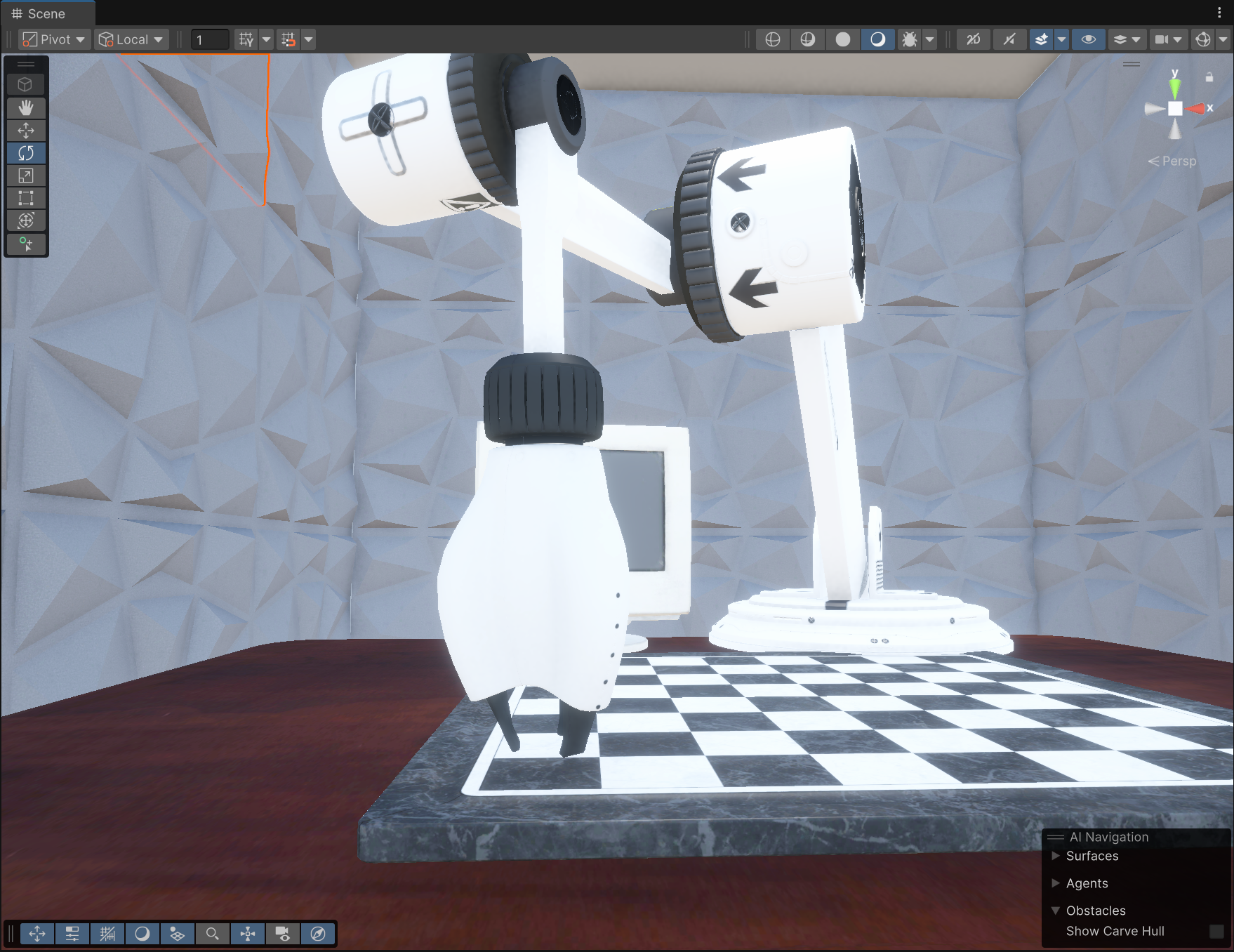
이미 축은 나눠져 있으니
간단하게 유니티에서 크기 따로따로 조절하여 해결
계획
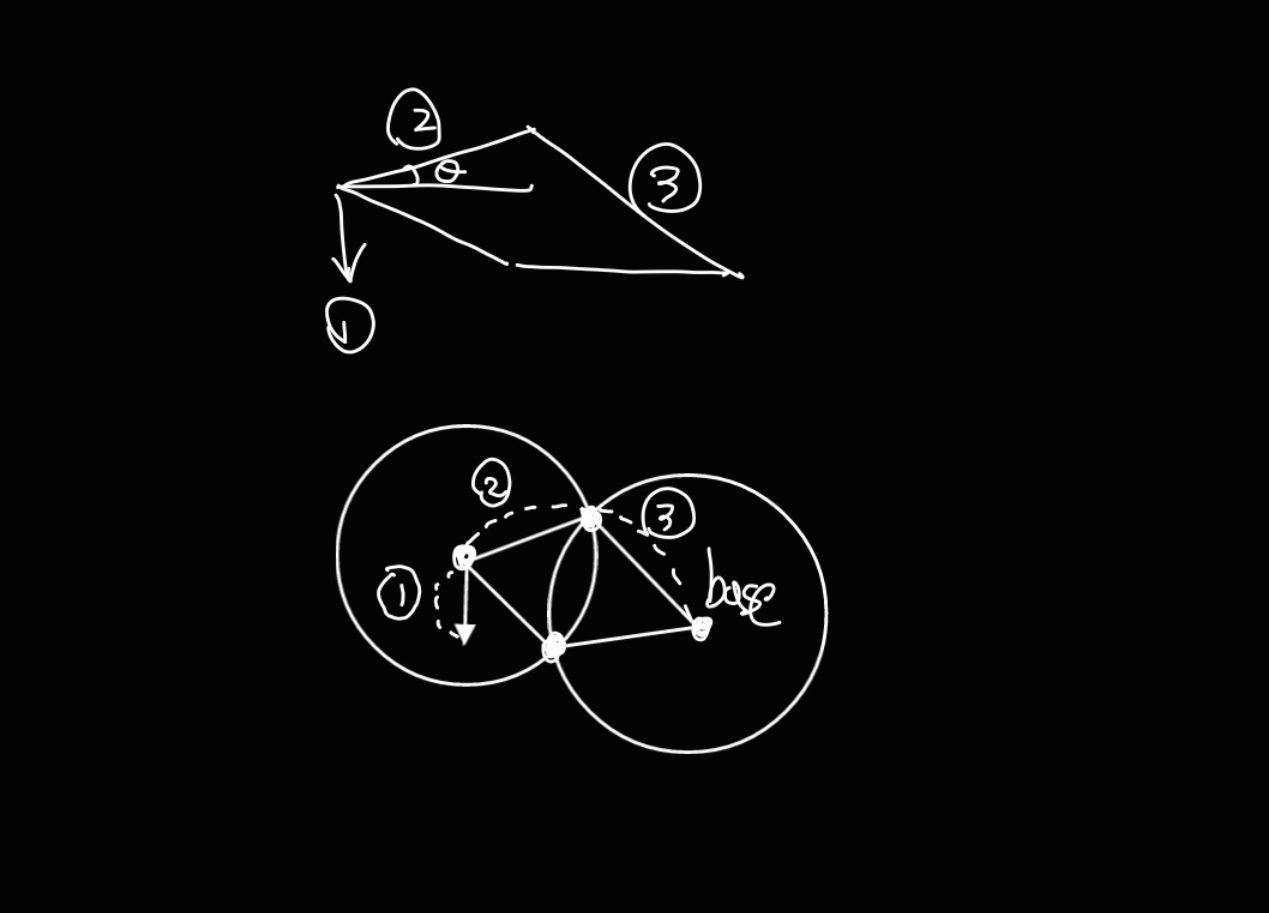
체스를 집어야 하는 1은 지면에 대해 수직 유지
2와 3은 각각 1의 시작점과 base의 시작점.
2와 3을 중심으로 한 두 원을 그리고 y 값이 더 높은 해를 고르기
z축 회전은 기물과 base을 이은 직선과 나란해질 때까지
알아야 하는 정보
- 체스 기물의 위치
- 1,2,3의 길이
- base의 위치
- 각 점의 월드 좌표계 기준 z축 회전
코드 설계
- 빈 게임 오브젝트 만들고 lookat으로 명명한 뒤에 LookAt()으로 바라보게 함
- base는 lookat의 z축 회전을 천천히 반영함
- 기물의 y 높이에서 (1)의 길이만큼 더한 곳을 중심으로 xy평면 (로컬 좌표계 기준) 의 원을 수식으로 표현
- base를 중심으로 하는 xy평면의 원을 수식으로 표현
- 두 원의 접점을 계산한 뒤, y값이 더 높은 해를 고름
- 해로 나온 점과 base의 atan로 (3)이 회전해야 할 각도를 구함
- 해로 나온 점과 기물의 y 높이에서 (1)의 길이만큼 더한 점의 atan로 (2)가 회전해야 할 각도를 구함
- 구해낸 각도들을 천천히 반영함
고려해야할 점

연결 부분들에 살짝씩 오프셋이 있음.
가로 오프셋은 그냥 더해주면 되는데 세로 오프셋은 접근이 어렵다.
이런거까지 계산에 넣으면 코드도 머릿속도 복잡해지기 때문에,
trial & error로 얼마만큼의 각도를 보정해줘야 하는지 알아낸 뒤 그냥 더해주기
계획 적어놓고도 어떻게 해야할지 감이 안 잡혀서 일단 가장 간단한 z축 움직임부터 차근차근 만들기
구현

void Update()
{
if (target == null) return;
Vector3 direction = target.position - y_axis_part.position;
direction.y = 0; // 불연속적 계산 방지
float angle = Vector3.SignedAngle(Vector3.forward, direction, Vector3.up);
y_axis_part.rotation = Quaternion.Euler(-90, 0, angle);
}y축 회전부터 시작
버그 : 중간에 불연속적으로 20도 정도 건너 뛰는 부분이 생김. y축 높이를 제거하여 xz평면의 벡터로 만들어 해결.
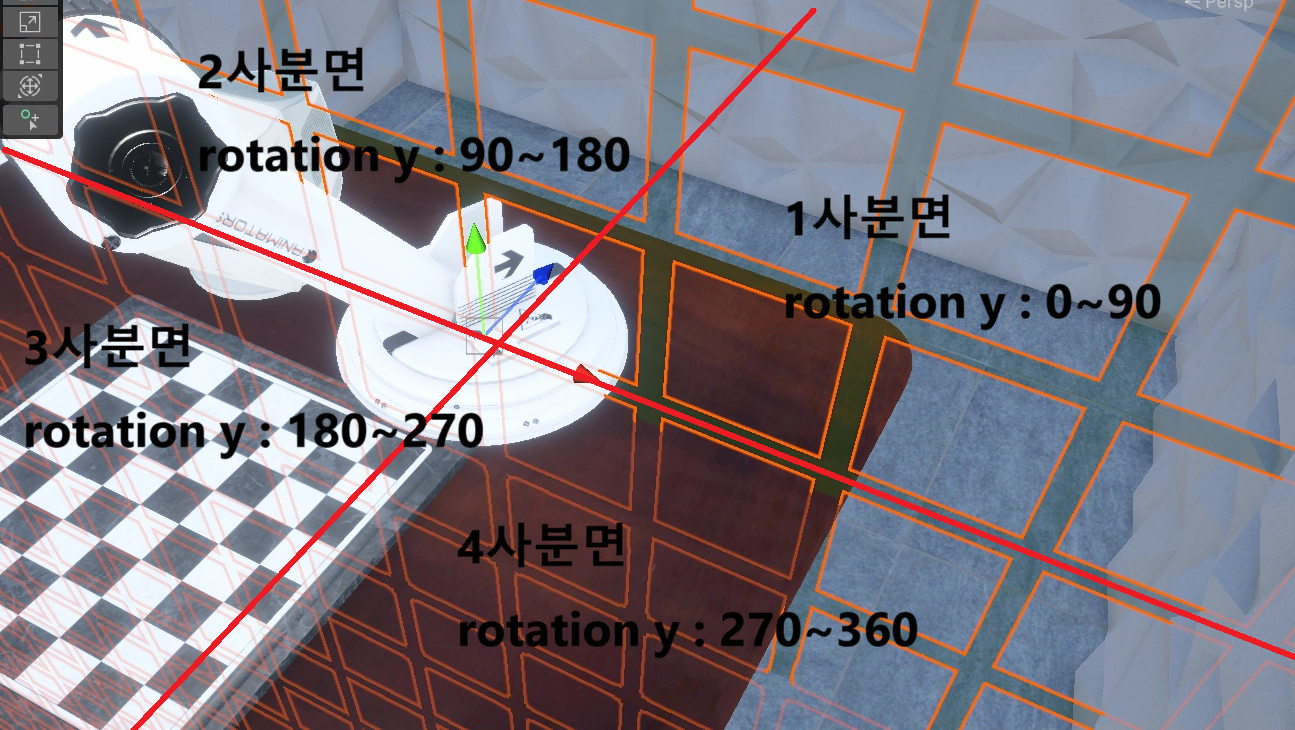
xz평면의 벡터를 법선 벡터로 갖는 z = nx 평면에 점들을 정사영시키고,
해당 평면에서 두 원의 교점 구한다.
n을 알아내기점들을 정사영시키기평면에서 계산하기계산한 점에서 다시 점들의 높이만큼 올려보내기
가 아니라,
평범한 2차원 평면 상에서 계산하고
그에 따라 각도가 나오면 반영하면 됨.
복잡하게 정사영이니 뭐니 할 필요 없음.
내일 마저 구현하기.
