To-do List
✅ 키워드 공부 | 그래프, BFS/DFS, 위상 정렬, B-Tree
✅ 백준 풀기 | 1991 트리 순회
🔴 Delayed
☑️ 정답 봤던거 직접 코딩해보기 | 사냥꾼, 하노이탑, nQueen
☑️ Do it! ~ 읽고 구현 연습 #자료구조 | 큐, 스택
☑️ Do it! ~ 읽고 구현 연습 #정렬 | 퀵 정렬(피봇 3선발), 병합 정렬, 힙 정렬
☑️ 슈도 코드 변환 | 버블 정렬, 이분 탐색, 백트래킹
배운 것들
함수 파라미터 초기화의 의미
def dfs_recursive(graph, start, visited=None):
(...)
dfs_recursive(graph, 'A')함수 자체에서 초기화 해주면 변수를 안 넣어도 초기화되어 있는 값으로 알아서 해준다
시간 복잡도
시간 복잡도는 최악의 경우를 고려하잖아, 그러면 두 개를 비교할 때 평균적으론 더 빠른데 시간 복잡도로는 더 긴 경우가 생기지는 않나? 이런거 표시하는 지표는 없나?
네, 두 알고리즘의 평균 성능이 서로 다를 수 있으며, 평균적으로는 더 빠를 수 있지만 최악의 경우 시간 복잡도는 더 긴 경우가 있을 수 있습니다. 이러한 차이를 명확히 하기 위해 다양한 성능 지표가 사용됩니다. 이들 지표는 알고리즘의 다양한 성능 측면을 평가합니다.
예시를 통한 설명
예를 들어, 퀵정렬(Quick Sort)과 병합정렬(Merge Sort)을 비교해 보겠습니다.
-
퀵정렬:
- 최악의 경우 시간 복잡도: O(n^2) (피벗이 항상 최악으로 선택될 때)
- 평균 시간 복잡도: O(n log n)
- 최선의 경우 시간 복잡도: O(n log n)
-
병합정렬:
- 최악의 경우 시간 복잡도: O(n log n)
- 평균 시간 복잡도: O(n log n)
- 최선의 경우 시간 복잡도: O(n log n)
이 경우, 병합정렬은 최악의 경우와 평균적으로 모두 O(n log n)입니다. 반면 퀵정렬은 최악의 경우 O(n^2)이지만 평균적으로는 O(n log n)입니다. 따라서 평균적으로 퀵정렬이 더 빠를 수 있습니다.
빅오, 빅세타, 빅오메가
찾아보니까 빅오 빅세타 빅오메가 이런걸로 표시한다는데 이거 설명좀
- 빅오 (Big O): 최악의 경우 성능을 나타내며, 알고리즘이 얼마나 오래 걸릴 수 있는지에 대한 상한을 제공합니다.
- 빅세타 (Big Θ): 평균적인 경우 성능을 나타내며, 알고리즘의 실행 시간이 입력 크기 n에 대해 어느 정도로 분포되는지를 설명합니다.
- 빅오메가 (Big Ω): 최선의 경우 성능을 나타내며, 알고리즘이 최소한으로 수행해야 하는 연산의 하한을 나타냅니다.
이 세 가지 표기법을 사용하면 알고리즘의 성능을 다양한 관점에서 평가할 수 있습니다. 일반적으로 빅오 표기법이 가장 많이 사용되지만, 빅세타와 빅오메가 표기법도 알고리즘의 성능을 더 잘 이해하는 데 도움이 됩니다.
그래프
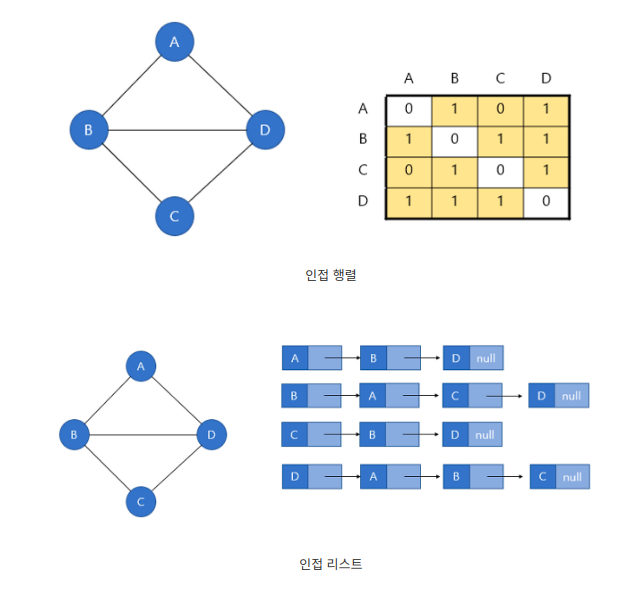
https://elisha0103.tistory.com/24
프로그래밍에서 그래프는 인접행렬, 인접리스트 방식으로 표현된다.
인접행렬: 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 메모리를 더 많이 쓰는 대신, 두 정점이 연결되었는지 확인하는 속도가 빠르다.
인접리스트: 리스트로 그래프의 연결 관계를 표현하는 방식
- 메모리를 덜 쓰는 대신에 두 정점의 연결 여부를 확인하는 데 시간이 걸린다.
간선의 개수가 많다면 인접 행렬이 유리하고, 간선의 개수가 적다면 인접 리스트가 유리하다.
그래프(vertex, edge, node, arc)
종류: Undirected, Directed, Weighted Graph
표현방식: 인접행렬(Adjacency Matrix), 인접리스트(Adjacency List)
이거 각각에 대해 자세하게 설명해줘
그래프(Graph)는 데이터 구조의 한 형태로, 정점(Vertex)과 그 정점을 연결하는 간선(Edge)으로 구성됩니다. 그래프는 정점(Node)과 간선(Arc)으로 표현될 수도 있습니다. 그래프의 종류와 표현 방식에 대해 자세히 설명하겠습니다.
그래프의 종류
-
무방향 그래프(Undirected Graph):
- 정점 간의 연결이 방향성을 가지지 않는 그래프입니다.
-
방향 그래프(Directed Graph):
- 정점 간의 연결이 방향성을 가지는 그래프입니다.
-
가중치 그래프(Weighted Graph):
- 각 간선에 가중치(Weight)가 부여된 그래프입니다.
그래프의 표현 방식
-
인접 행렬(Adjacency Matrix):
- 행렬의 각 요소 (i, j)는 정점 i에서 정점 j로의 간선이 있는지 여부를 나타냅니다. 간선이 있으면 1(또는 가중치 값), 없으면 0으로 표시합니다.
- 장점: 두 정점 간의 간선 존재 여부를 O(1) 시간에 확인할 수 있습니다.
- 단점: 메모리 사용량이 많으며, 간선 수가 적은 희소 그래프(Sparse Graph)에서는 비효율적입니다.
예시:
A B C A 0 1 0 B 1 0 1 C 0 1 0 -
인접 리스트(Adjacency List):
- 각 정점에 대해 해당 정점과 연결된 모든 정점을 리스트로 저장합니다.
- 장점: 메모리 사용량이 적으며, 간선이 적은 그래프에서 효율적입니다.
- 단점: 두 정점 간의 간선 존재 여부를 확인하는 데 O(n)의 시간이 걸릴 수 있습니다.
예시:
A: B B: A, C C: B
깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)
깊이 우선 탐색(DFS)
아래 레벨에 방문 안 한 노드가 있으면 그 노드를 우선 탐색
한 놈만 팬다
- 특정 경로가 존재하는지, 또는 모든 경로를 찾는 문제에 유용
- 그래프에서 사이클이 있는지 검사할 수 있다
- 재귀나 스택으로 구현한다
- 결과 하나를 만들어낸 뒤 다음 결과를 만들러 가기 때문에 검증하기가 쉽다
넓이 우선 탐색(BFS)
레벨별로 탐색한다
여러 놈을 한 대씩 때리며 간다
- 무방향 그래프에서 시작 정점에서 다른 정점까지의 최단 경로 찾을 수 있음
- 큐나 링크드 리스트를 사용한다
- DFS에 비해 경로 운빨을 덜 탄다 (시간 복잡도가 낮다)
문제 유형
- 경로탐색 유형 (최단거리, 시간)
- 네트워크 유형 (연결)
- 조합 유형 (모든 조합 만들기)
gpt 구현
bfs, dfs 파이썬 구현 보여줘
BFS (Breadth-First Search) 구현
from collections import deque
def bfs(graph, start):
visited = set() # 방문한 노드를 기록할 집합
queue = deque([start]) # 시작 노드를 큐에 삽입
visited.add(start)
while queue:
vertex = queue.popleft() # 큐에서 노드를 하나 꺼냄
print(vertex, end=" ") # 방문한 노드를 출력
for neighbor in graph[vertex]:
if neighbor not in visited:
queue.append(neighbor) # 인접한 노드를 큐에 삽입
visited.add(neighbor) # 방문한 노드로 표시
# 그래프 예제 (인접 리스트)
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# BFS 실행
print("BFS:")
bfs(graph, 'A')DFS (Depth-First Search) 구현 - 재귀 방식
def dfs_recursive(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start, end=" ") # 방문한 노드를 출력
for neighbor in graph[start]:
if neighbor not in visited:
dfs_recursive(graph, neighbor, visited)
# DFS 실행 (재귀 방식)
print("\nDFS (Recursive):")
dfs_recursive(graph, 'A')DFS (Depth-First Search) 구현 - 스택 사용
def dfs_stack(graph, start):
visited = set() # 방문한 노드를 기록할 집합
stack = [start] # 시작 노드를 스택에 삽입
while stack:
vertex = stack.pop() # 스택에서 노드를 하나 꺼냄
if vertex not in visited:
print(vertex, end=" ") # 방문한 노드를 출력
visited.add(vertex)
for neighbor in graph[vertex]:
if neighbor not in visited:
stack.append(neighbor) # 인접한 노드를 스택에 삽입
# DFS 실행 (스택 사용)
print("\nDFS (Stack):")
dfs_stack(graph, 'A')코드 설명
-
BFS 구현:
deque를 사용하여 큐를 구현합니다.- 시작 노드를 큐에 삽입하고, 큐가 빌 때까지 반복하여 노드를 하나씩 꺼내고 인접한 노드를 방문합니다.
-
DFS 재귀 방식 구현:
- 재귀 호출을 통해 그래프를 깊이 우선으로 탐색합니다.
- 방문한 노드를 기록하고, 인접한 노드를 재귀적으로 호출합니다.
-
DFS 스택 사용 구현:
- 스택을 사용하여 깊이 우선 탐색을 수행합니다.
- 시작 노드를 스택에 삽입하고, 스택이 빌 때까지 반복하여 노드를 하나씩 꺼내고 인접한 노드를 방문합니다.
이거 그냥 탐색 과정을 보여주는거잖아 이거 말고 트리 경우의수들 보여주게 코드 바꿔줘
from collections import deque
def bfs_all_paths(graph, start):
paths = [] # 모든 경로를 저장할 리스트
queue = deque([(start, [start])]) # (현재 노드, 경로) 튜플을 큐에 삽입
while queue:
(vertex, path) = queue.popleft() # 큐에서 노드와 경로를 꺼냄
for neighbor in graph[vertex]:
if neighbor not in path: # 방문한 적이 없는 노드만
new_path = path + [neighbor] # 새로운 경로 생성
queue.append((neighbor, new_path)) # 큐에 삽입
paths.append(new_path) # 경로를 저장
return paths
# 그래프 예제 (인접 리스트)
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# BFS를 사용하여 모든 경로 찾기
print("All BFS Paths:")
all_paths = bfs_all_paths(graph, 'A')
for path in all_paths:
print(" -> ".join(path))위상 정렬
https://m.blog.naver.com/ndb796/221236874984
가능한 경로 한 가지를 출력하는 알고리즘
진입차수와 진출차수
- 진입차수 (Indegree) : 특정한 노드로 들어오는 간선의 개수
- 진출차수 (Outdegree) : 특정한 노드에서 나가는 간선의 개수
B-Tree
https://www.youtube.com/watch?v=K1a2Bk8NrYQ
키 여러 개 넣고 부모 노드의 키들 사이에 있는 수들은 부모 노드에 넣는다
최소 신장 트리
부분 그래프 : 주어진 그래프에서 일부 정점과 간선만을 택해서 구성한 새로운 그래프
신장 트리 : 주어진 방향성이 없는 그래프의 부분 그래프(subgraph)들 중에서 모든 정점을 포함하는 트리
- 정점이 N개인 그래프에서 신장 트리는 N-1개의 간선을 갖는다
- 주어진 그래프가 연결 그래프일 때만 신장 트리가 존재
최소 신장 트리 : 신장 트리 중 간선의 합이 최소인 트리
크루스칼 알고리즘
- 간선 데이터를 비용에 따라 오름차순으로 정렬
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킴
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않음
- 모든 간선에 대해 2번의 과정을 반복
백준
1991 트리 순회
import sys
input = sys.stdin.readline
N = int(input())
nodes = {}
for _ in range(N):
X, Y, Z = input().split()
nodes[X] = Y, Z
def preorder(key):
if nodes[key][0] == '.' and nodes[key][1] == '.':
return
print(key)
if nodes[key][0] != '.': preorder(nodes[key][0])
if nodes[key][1] != '.': preorder(nodes[key][1])
preorder('A')3문제를 내리 답지만 봤다.
답지를 보고 과정을 보면 이해가 가지만
백지에서 구현하라고 하면 전혀 할 수가 없을 것 같았다.
전혀 발전하지 않는 느낌이 들어서 첫 문제를 내 힘으로 풀어봤다.
답지를 봤던거라 완벽히 내 힘만으로 푼 건 아니지만.
자꾸 남들이 앞서나가는 느낌이 드니까 조급해져서 답지를 봐버린다.
자연스럽게 다음 문제를 풀 힘도 길러지질 않는다.
문제를 풀기 위해 구현해보려는 노력을 해야 실력이 길러질 것 같다.
import sys
input = sys.stdin.readline
N = int(input())
nodes = {}
for _ in range(N):
X, Y, Z = input().split()
nodes[X] = Y, Z
def preorder(key):
if key != '.':
print(key, end='')
if nodes[key][0] != '.': preorder(nodes[key][0])
if nodes[key][1] != '.': preorder(nodes[key][1])
preorder('A')위는 내가 푼 코드, 이건 답지를 보고 고쳐본 코드.
아직 시간은 있으니 지금이라도 방향성을 고치면 된다.
