🧭 To-do List
✅ 백준 풀기 | 5639 이진 검색 트리, 1197 최소 스패닝 트리
✅ 키워드 공부 | 트라이(Trie), 다익스트라
📝 배운 것들
🏷️ General
class Node(object):
여기서 object가 뭐임?
- 파이썬 2.x에서는 클래스가 object를 상속받아야 새로운 스타일의 클래스로 정의됩니다. 하지만 파이썬 3.x에서는 모든 클래스가 자동으로 object를 상속받으므로 (object) 부분을 생략할 수 있습니다. 즉, class Node:라고 정의해도 동일합니다.
제네릭 프로그래밍
하나의 자료형에만 의존하지 않고 공통 속성을 갖는 여러 자료형에 대해 동일하게 작동하는 알고리즘을 작성하는 기법 일반을 의미. 파이썬은 애초에 동적 타이핑 언어이기 때문에 제네릭을 따로 구현할 필요가 없다.
코드 줄바꿈 시키는 법
방법 1: 백슬래시()를 사용하여 줄바꿈
if f_find is not None \
and s_find is not None \
and f_find == s_find:
# 실행할 코드 블록
pass방법 2: 소괄호 ()를 사용하여 줄바꿈
if (f_find is not None
and s_find is not None
and f_find == s_find):
# 실행할 코드 블록
pass🏷️ 트라이(Trie)
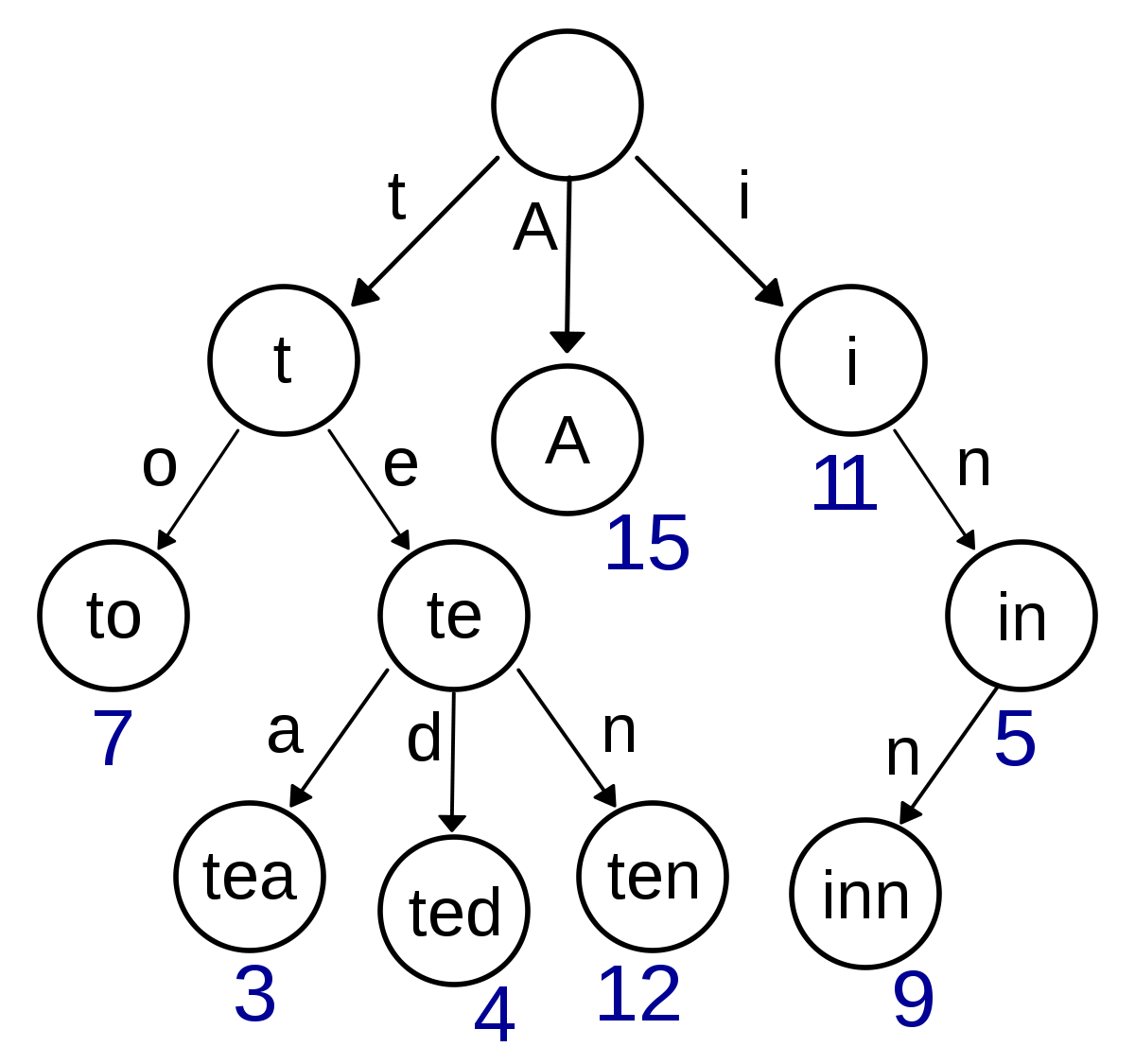
트라이 : 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조
- 'Datastructure'라는 단어를 검색하기 위해서는 제일 먼저 'D'를 찾고, 다음에 'a', 't', ... 의 순서로 찾으면 된다.
예시: abc 삽입
- 'a'를 head에 추가
- 'a'노드에 자식이 하나도 없으므로 자식으로 'b' 추가
- 'c'도 마찬가지로 'b'에 추가
- 'abc'가 여기서 끝남을 알리기 위해 현재 노드에 'abc'라고 표시(Data)
구현
Node
class Node:
def __init__(self, key, data=None):
self.key = key
self.data = data
self.children = {}- key : 해당 노드의 문자
- child : 자식 노드
- data : 문자열이 끝나는 위치
class Trie(object):
def __init__(self):
self.head = Node(None)
# def 문자열 삽입
# 삽입할 String 각각의 문자에 대해 자식 Node를 만들며 내려간다.
# 자식 Node들 중 같은 문자가 없으면 Node 새로 생성
# 같은 문자가 있으면 노드를 따로 생성하지 않고, 해당 노드로 이동
# 문자열이 끝난 지점의 노드의 data값에 해당 문자열을 표시
# def 문자열 탐색
# 가장 아래에 있는 노드에서부터 탐색 시작한다.
# 탐색이 끝난 후에 해당 노드의 data값이 존재한다면
# 문자가 포함되어있다는 뜻이다🏷️ 다익스트라(Dijkstra) 알고리즘
- 출발 노드와 도착 노드를 설정
- '최단 거리 테이블'을 초기화
- 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고,
방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다. - 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트
⚔️ 백준
📌 5639 이진 검색 트리
from __future__ import annotations
from typing import Any, Type
import sys
sys.setrecursionlimit(10**5)
class Node:
def __init__(self, value, left: Node = None, right: Node = None):
self.value = value
self.left = left
self.right = right
class BST:
def __init__(self):
self.root = None
def add_node(self, value):
# 루트에 노드가 없으면 루트 생성
if self.root is None:
self.root = Node(value)
return
# 루트에서부터 탐색 시작
p = self.root
# 현재 노드보다 값이 크면 왼쪽,
# 값이 작으면 오른쪽으로 가기
while True:
# 넣을 값이 현재 노드 값보다 작으면
if value < p.value:
# 왼쪽 자식이 없으면 노드 추가
if p.left == None:
p.left = Node(value)
break
# 왼쪽 자식이 있으면 포인터 변경
else:
p = p.left
# 넣을 값이 현재 노드 값보다 크면
elif value > p.value:
# 오른쪽 자식이 없으면 노드 추가
if p.right == None:
p.right = Node(value)
break
# 오른쪽 자식이 있으면 포인터 변경
else:
p = p.right
def postorder(self, p):
if p == None:
return
self.postorder(p.left)
self.postorder(p.right)
print(p.value)
bst = BST()
while True:
try:
bst.add_node(int(input()))
except:
break
bst.postorder(bst.root)이진 트리를 직접 구현해서 풀어봤다.
BST 클래스 만든 후에 인스턴스를 만들어줘야 하는 걸 배웠다.
천천히 생각하면서 구현해보니까 자력으로 풀 수 있었다.
앞으로도 이런 느낌으로 풀면 될 것 같다.
이제야 실력이 좀 늘어나는 느낌이 든다.
📌 1197 최소 스패닝 트리
# 크루스칼 알고리즘
# 1. 간선 데이터를 비용에 따라 오름차순으로 정렬
# 2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인
# 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킴
# 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않음
# 3. 모든 간선에 대해 2번의 과정을 반복구현해야 하는 것
# 아무것도 없으면 간선 추가
if len(unions) == 0:
unions.append(edge)
return
# 서로소 집합들 탐색
for union in unions:
f_check = False
s_check = False
for vertex in union:
if vertex == edge[0]:
f_check = True
elif vertex == edge[1]:
s_check = True
# 간선 이루는 정점 2개가 특정 유니온에 있었다면
if f_check and s_check:
break
if f_check and s_check:
# 사이클이 발생한 것
return
else:
# 사이클이 발생하지 않음시도 (1) : union 여러 개 만들어서 해보려고 함
def kruskal(edge):
# 유니온 길이 0이면
if len(unions) == 0:
unions.append([edge[0],edge[1]])
return edge[2]
f_union = None
s_union = None
for union in unions:
# 유니온 원소 확인
for element in union:
if element == edge[0]:
f_union = union
elif element == edge[1]:
s_union = union
if (f_union is not None
and s_union is not None
and f_union == s_union):
if
break
# 사이클 안 생기면 간선 추가하고 가중치 더하기
unions.append([edge[0],edge[1]])
return edge[2]시도 (2) : union 한 개 만들어서 해보려고 함
import sys
input = sys.stdin.readline
V, E = map(int, input().split())
Edges = []
for _ in range(E):
A, B, C = map(int, input().split())
Edges.append([A, B, C])
def third_val(e):
return(e[2])
Edges.sort(key = third_val)
# 각 정점이 들어있는 유니온을 기록함
union = [i for i in range(V)]
def kruskal(edge):
s = union[edge[0]-1]
e = union[edge[1]-1]
if s == e:
return 0
else:
for i in range(V):
if union[i] == s:
union[i] = e
return edge[2]
result = 0
for edge in Edges:
result += kruskal(edge)
print(result)맞은 코드.
각 정점이 속해있는 유니온을 숫자로 추상화해서 풀었다.
리스트를 딕셔너리로 바꾼다던가 하면 더 빨라질듯?
지금은 유니온을 정점 개수만큼 선언한 뒤에 매번 훑어서 좀 느리다.
