FPCV 4주차, Edge Detection & Boundary Detection

개요

• First Principles of Computer Vision 스터디 정리용 글
• ECCV Rebuttal과 Neurips 때문에 2주 쉬고 다시 시작
• 4주차는 Edge Detection과 Boundary Detection을 들음

Edge Detection

Overview

• Video Link
• Topics
• What is Edge? 정의, 좋은 edge detector는 어때야하는가?
• Edge Detection Using Gradients
• Edge Detection Using Laplacian
• Canny Edge Detector (hybrid!)
• Corner Detection, 두 엣지가 만나는 곳은?, Harris Corner Detector

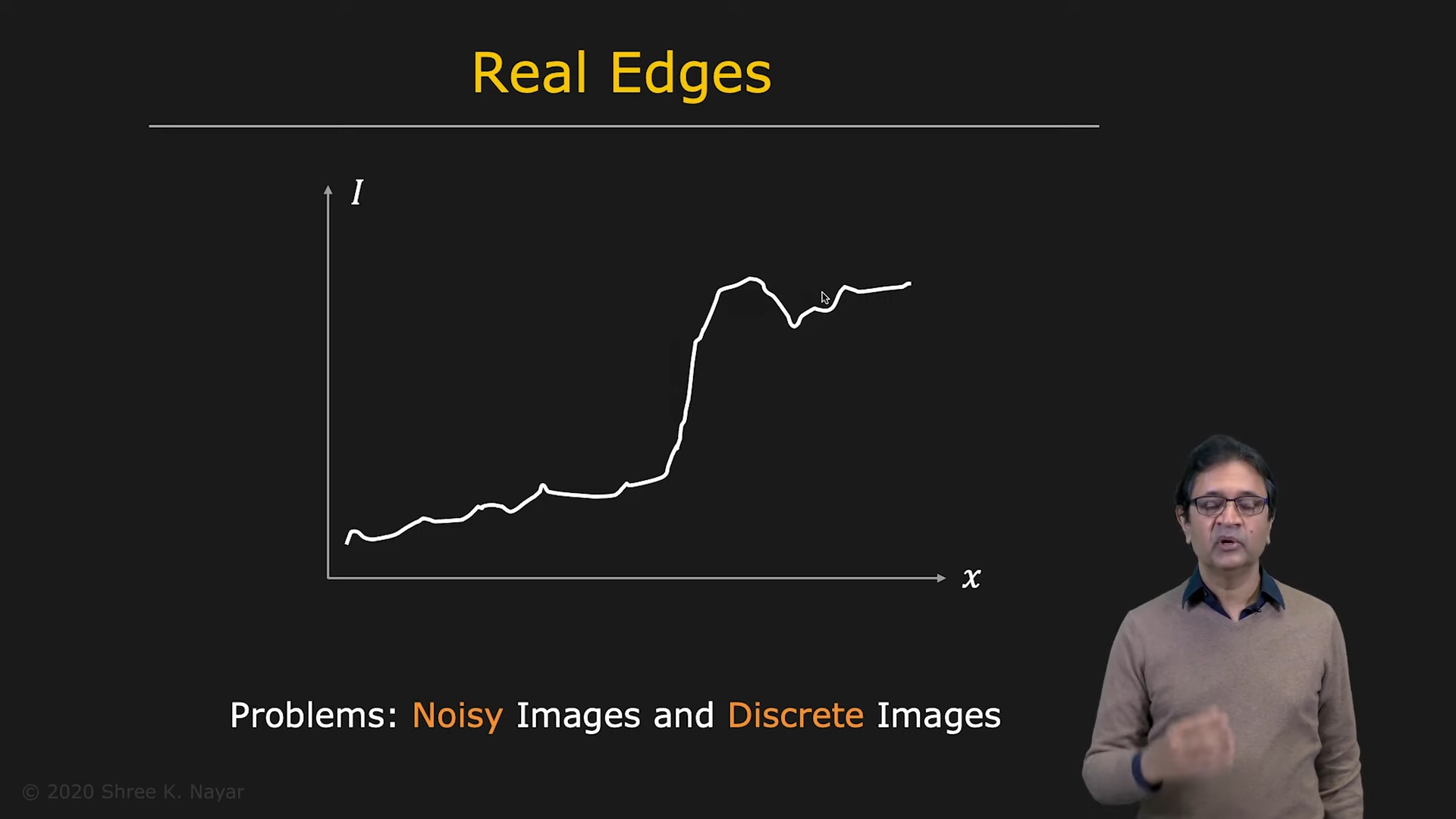
What is Edge?

• Video Link
• navie하게 정의해보면 image intensity(brightness)의 좁은 영역에서의 급격한 변화
• edge의 원인들
  • surface normal discontinuity
  • depth discontinuity
  • surface reflectance discontinuity
  • illumination discontinuity
• 다양한 intensity function을 통해 edge를 modeling할 수 있다

edge의 원인들	edge model들

문제는 현실의 edge는 이상적이지 않다	그래서 좋은 edge detector는 이래야한다

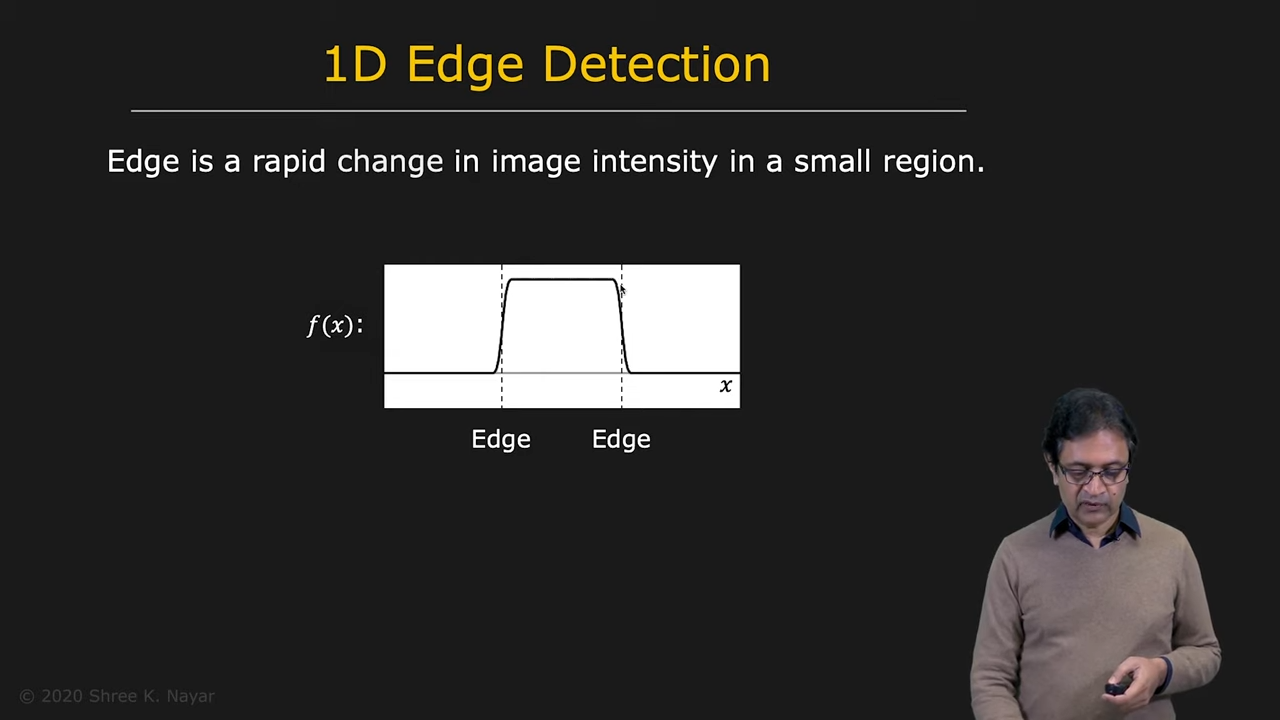
Edge Detection Using Gradients

• Video Link
• 우리가 찾는 edge는 intensity의 급격한 변화이기에 1st derivative를 쓰는 것은 straight-forward하다

edge의 intensity 변화	1st derivative의 absolute value

• 하지만 우리는 image를 다루고 있기 때문에 2d에 대해 고려해야한다. 그래서 partial derivative와 gradient가 등장.

2d edge	gradient의 활용

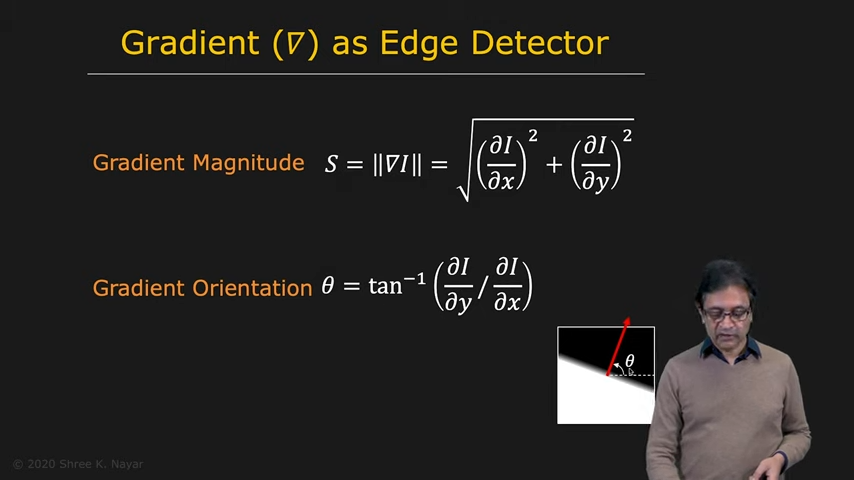gradient의 magnitude와 orientation 활용	Dscrete Gradient는 Convolution을 활용할 수 있다

• sobel edge filter가 오랬동안 사용되어 왔으며, 이는 여러 상황에서 다양하게 활용가능하다

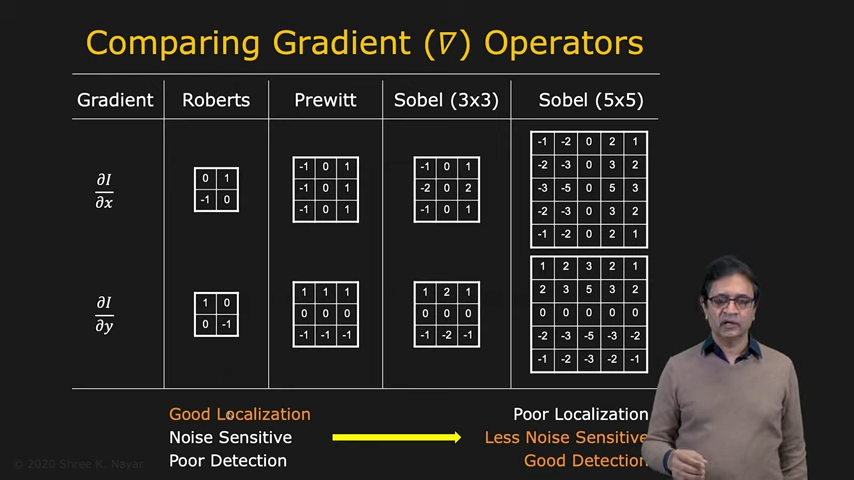다양한 convolution kernel과 size에 따른 변화	마지막으로 edge를 thresholding할 때 어떻게 할지 생각해볼 수 있다

Edge Detection Using Laplacian

• Video Link

2nd derivative도 당연히 쓸 수 있다	Laplacian이 여기서 등장한다

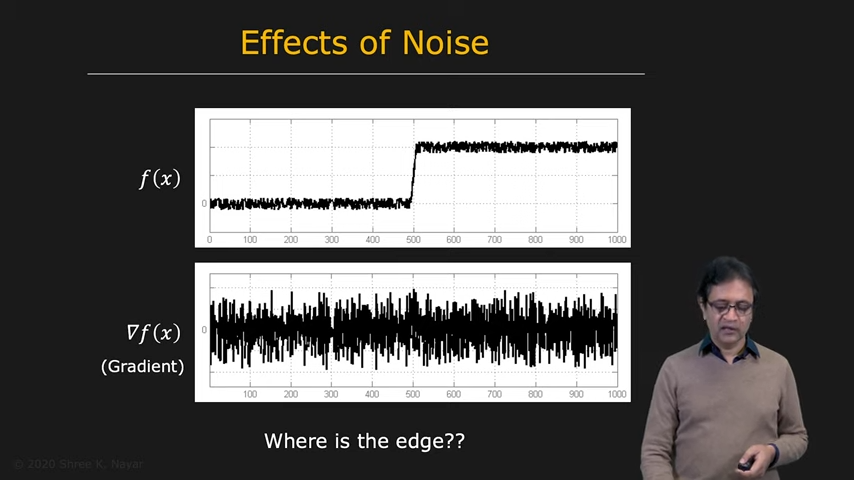discrete laplacian도 convolution을 활용할 수 있다	Noise는 1st derivative에 영향을 미친다

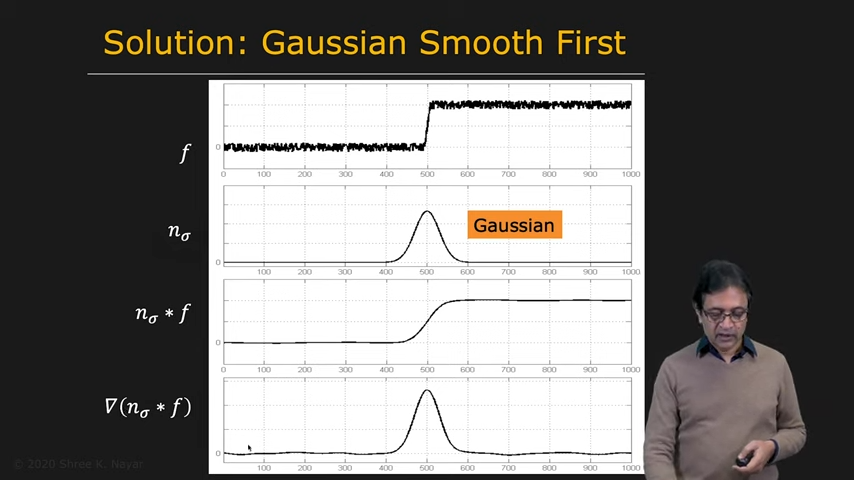
• Noise를 해결하는 solution은 gaussian에 있다
• image를 gaussian할수도 있고, kernel을 gaussian할 수도 있다

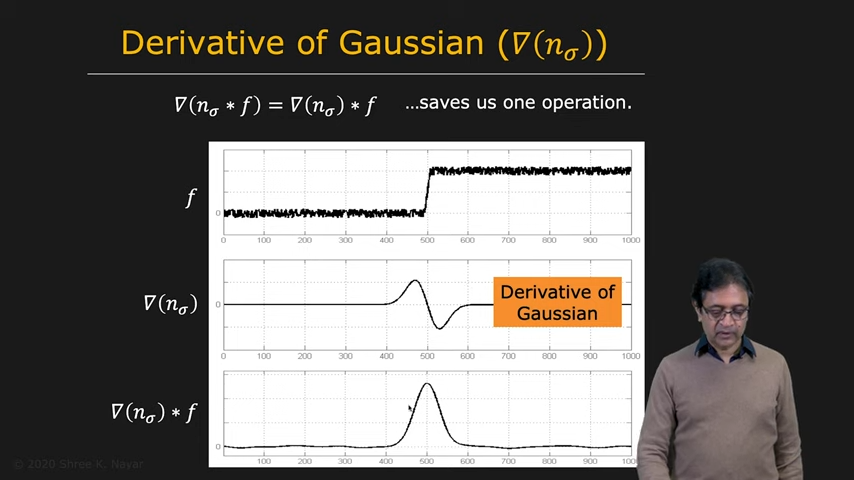
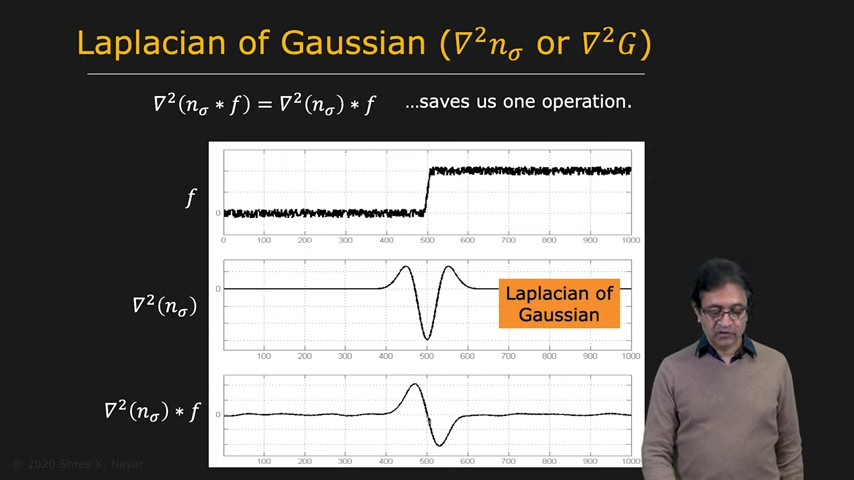
Gaussian First	Gaussian의 1st derivative	Gaussian의 2nd derivative

gradient와 laplacian의 차이	각각의 edge detector의 차이

• 둘의 장점을 각각 활용하는 canny edge detector를 알아보자

Canny Edge Detector

• Video Link
• gaussian smoothing하고 sobel filter를 적용하고 gradient magnitude와 orientation을 구하고 이를 이용해 edge를 판별한다
• 오래 걸리지만 가장 많은 정보를 주고 다양한 상황에서 강인하게 동작한다

canny edge detector	hyper-parameter에 따른 결과 차이

Corner Detection

• Video Link
• Edge가 만나는 곳이 Corner다

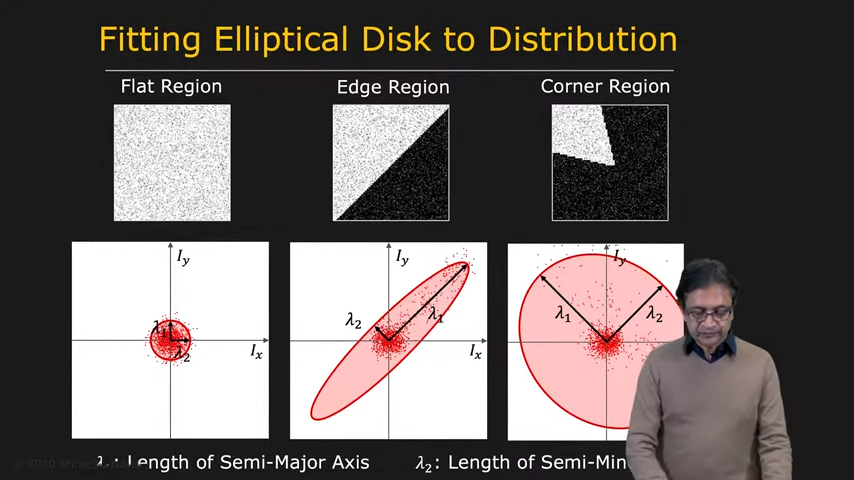
당연하게도 이번에도 gradient를 쓸 수 있다	주요 아이디어는 image gradient의 distribution을 활용

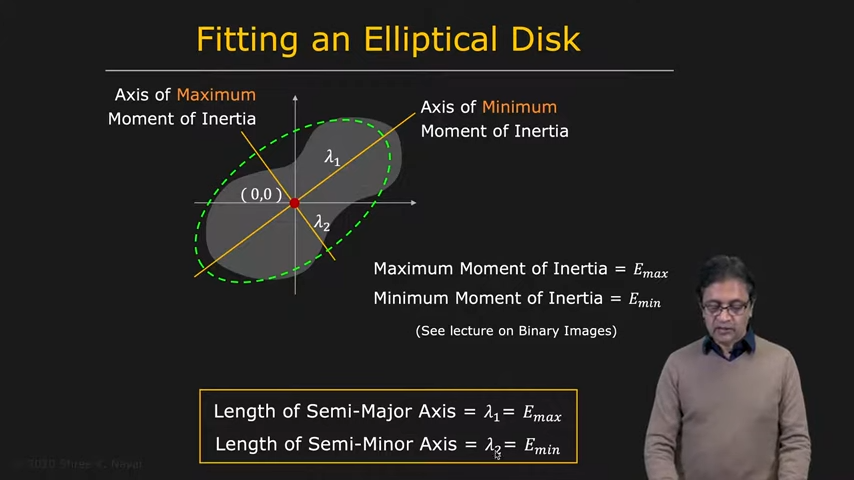
lambda 1,2를 찾아내면 쓸 수 있다	요런 식으로 찾을 수 있다

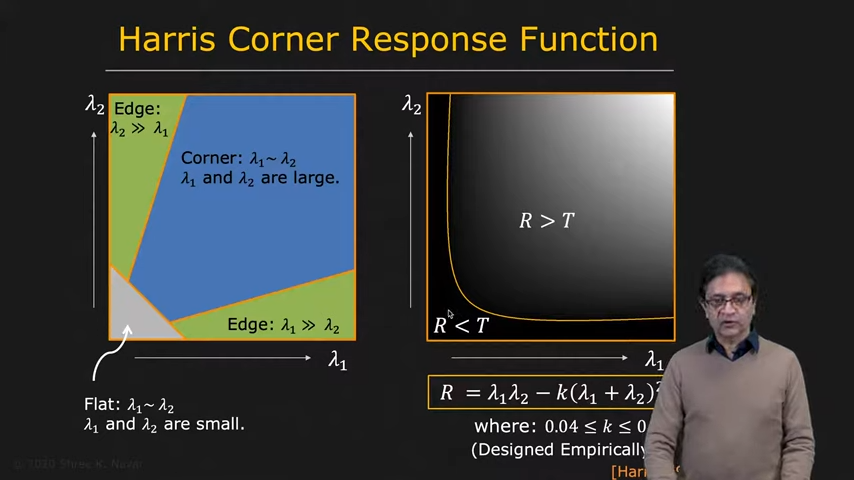
lambda 1,2를 활용한 해석	Harris Corner Response Function

Naive Harris Corner Detection의 예시	Peak Value를 찾는 방법, Non-Maximal Surppression

Boundary Detection

Overview

• Video Link
• Topics
• Fitting Lines and Curves to Edges
• Active Contours (Snakes)
• The hough Trasnform : Solve Inliner-Outlier Problem
• The generalized hough trasnform

Fitting Lines and Curves

• Video Link

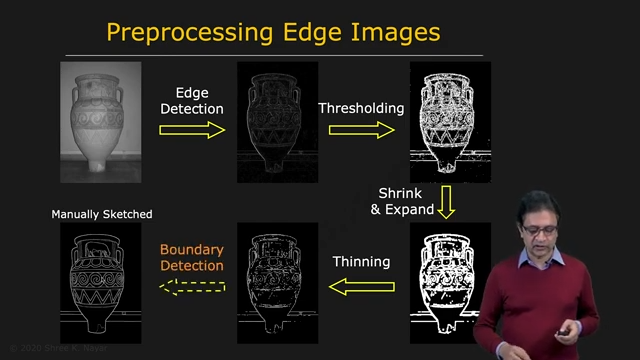
Boundary Detection의 목표	문제 해결의 방향성 vertical distance 말고 perpendicular distance

문제 해결의 방향성 원하는 수준의 곡선에 fitting	Solve Linear System

Active Contour

• Video Link

Active Contour의 정의	왜 이런 일을 하는가? Tracking 등에 유용하다

Contour를 표현하는 방법 set of points	Blurred Gradient를 활용해서 point를 edge로 끌어당길 수 있다

위의 아이디어들을 기반으로 Greedy Algorithm을 구현할 수 있다. 하지만 Noise에 약하고 느리다	이를 해결하기 위해 internal bending energy 아이디어를 도입할 수 있다

이렇게 계산할 수 있다	업데이트된 알고리즘은 다음과 같다

결과 예시는 다음과 같다	이 과제들과 방법론들에서 생각해볼점

Hough Transform

• Video Link
• TODO

TODO

TODO