FPCV 3주차, Image Processing 1&2

개요

• First Principles of Computer Vision 스터디 정리용 글
• 3주차는 Image Processing 1&2를 들음

Image Processing 1

Overview

• Video Link
• 이미지를 분석하기 쉽도록 더 깔끔하거나 쉬운 형태로 변형하는 법을 배운다
• e.g. motion blur를 없애기
• e.g. defocus blur를 없애기
• e.g. edge나 corner를 찾기를 바랄 수 있다
• Topics
  • Pixel Processing (brightness, color, ...)
  • Linear Shift Invariant System (LSIS) and Convolution
  • Linear Image Filters
  • Non-Linear Image Filters
  • Template Matching by Correlation
  • Q. Convolution과 Correlation의 관계는?

Pixel Processing

• Video Link
• Image는 Function으로 생각할 수 있다 (r,b,g) = I(x,y)
• function은 mapping 시킬 수 있다 g(x,y) = T(f(x,y))

Point Processing의 예시	Point Processing의 예시 2

LSIS and Convolution

• Video Link
• LSIS 연구는 매우 많은 유용한 image processing algorithm을 만들어냈다

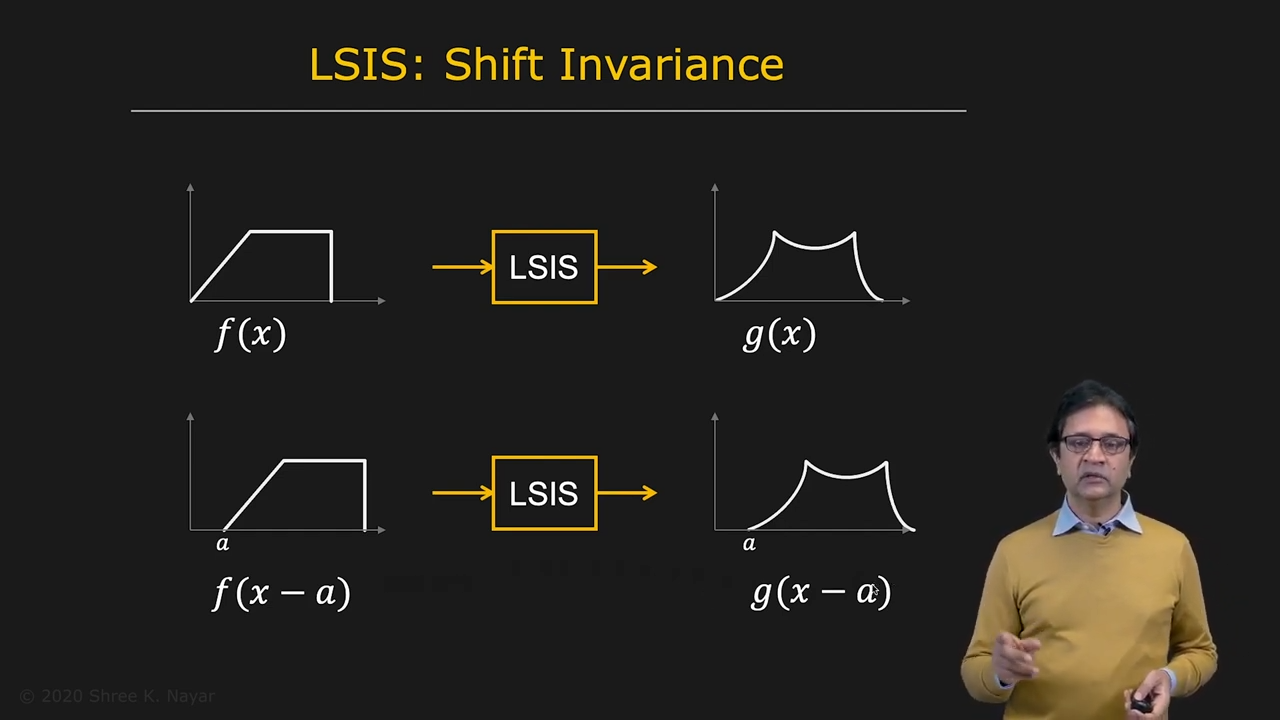
Linearity에 대한 설명	Shift-Invariant에 대한 설명

이게 왜 중요하냐면 이론적으로 렌즈는 LSIS다

• convolution은 공학을 한다면 결국 알고 있을 수 밖에 없다
• convolution은 두 함수 사이의 연산이며 f를 h로 convolution한다는 것은 h를 sliding하며 f와 적분한 값을 구한다는 것이다, 시각화 영상

convolution의 정의

• 중요한건 LSIS는 convolution이 암시적으로 어딘가에 존재한다는 것, 반대로 convolution을 수행하고 있다면 이는 LSIS임을 의미한다
• convolution 연산이 linearity를 가지고 있고 shift-invariant함을 보일 수 있다
• LSIS 시스템이 있을 때 f convolution h = g h를 어떻게 알아낼 수 있을까?

convolution에 대한 항등원은 unit impulse function (delta function)이다	항등원을 이용하면 h를 알아낼 수 있다

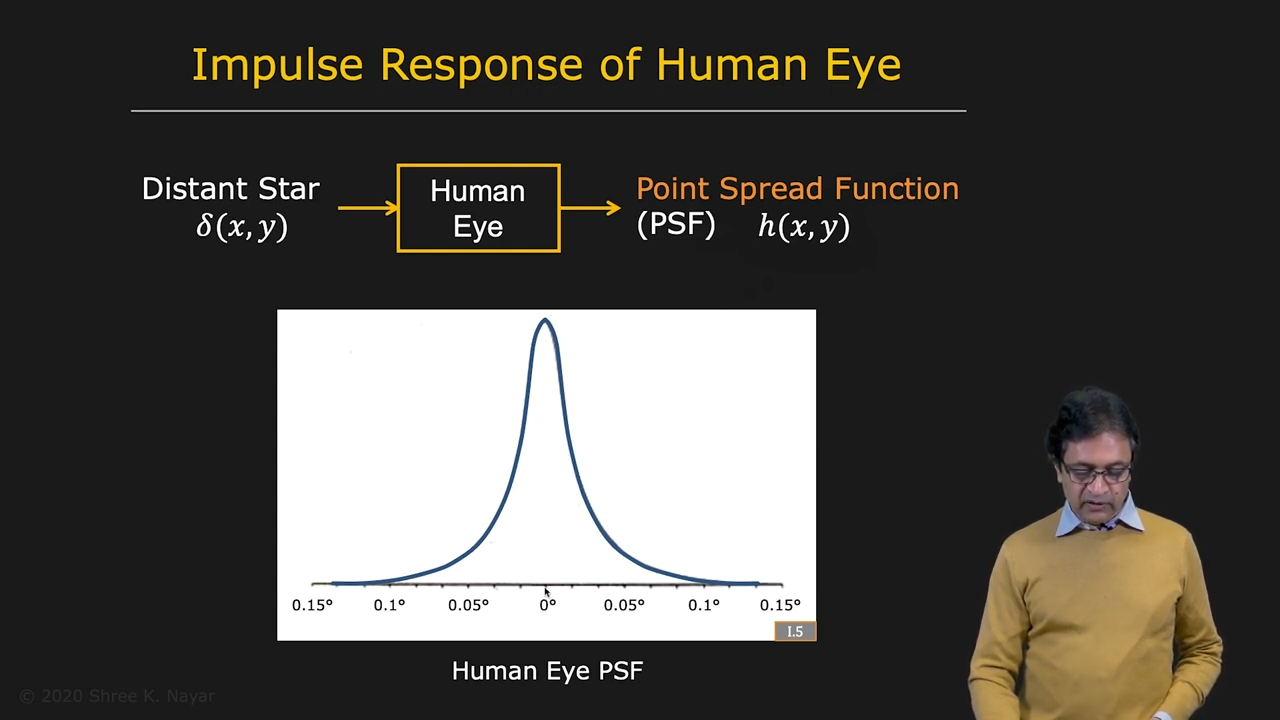
사람의 눈의 convolution function

• convolution은 commutative (교환법칙), associative (결합법칙)이 성립한다
• 두 개의 convolution system은 합쳐지거나 순서를 바꿔서 적용해도 된다
• 2D Convolution은 이중적분을 활용한다, 3D, ... n-d까지도 모두 잘 적용된다

Linear Image Filters

• Video Link
• 우리가 하는건 image pixel에 대한 2D discrete convolution이다, 시각화 영상
• 적분이 아닌 구간합을 활용, kernel=mask=filter를 활용
• Border Problem이 있기 때문에 이를 해결하기 위해 (1) ignore border (2) pad with contant value (3) pad with reflection

예시 : impulse function	예시 : translation

예시 : Box Filter(sum)	예시 : Box Filter(average)

예시 : Box Filter(smoothing)	예시 : Fuzzy Filter(smoothing)

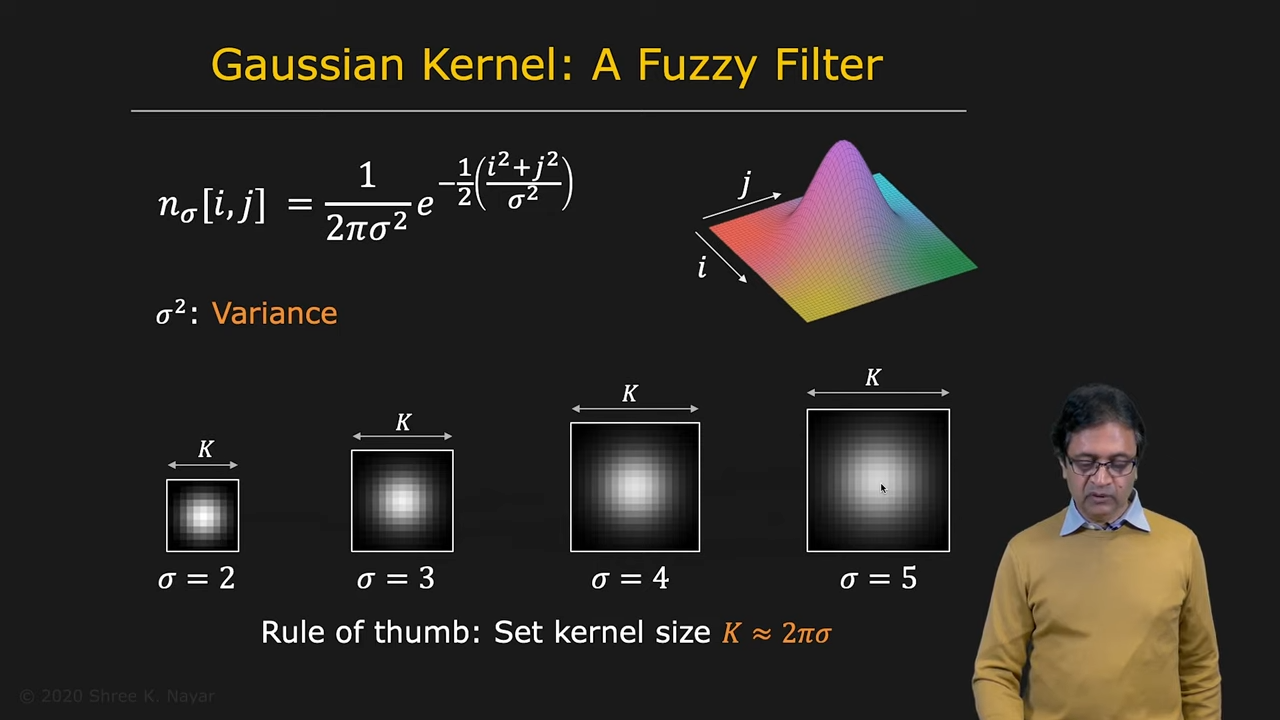
• Gaussian Kernel이 Fuzzy Filter로써 아주 훌륭하며 sigma와 kernel size의 조정을 통해 원하는 smoothing이 가능하다
• 2D Gaussian Smoothing은 두 개의 1D Gaussian Smoothing으로 seperable하다

다양한 gaussian kernel	Seperated Gaussian Kernel

Non-Linear Image Filters

• Video Link
• Salt and Pepper Noise는 Linear Image Filter로 처리할 수 없는 전형적인 예시, linear filter는 outlier에 대응하기 어렵다 (XOR problem)
• 이를 해결하기 위한 예시로 Median Filter가 있다

Median Filter의 적용 예시	Median Filter의 한계

• 하지만 Median Filter도 일반적인 noise에는 제대로 대응하기 어렵다
• Gaussian Smoothing의 문제점을 살펴보면 모든 곳에서 blur해버려서 edge와 같은 정보가 사라진다는 것이다, context-aware하게 하는 방법은 없을까?

간단한 해결 책 중 하나

• 이런 bias를 넣어보자는 idea에서 출발한 게 bilateral filter
• spatial gaussian뿐 아니라 brightness gaussian term을 추가해서 우리가 원하는 부분에만 spatial gaussian을 적용한다
• spatial gaussian과 brightness gaussian의 sigma 변화를 통해 원하는 결과를 조정할 수 있다
• brightness gaussian의 sigma가 infinite일 경우 gaussian filter와 동일하다

bilateral filter의 시각화	Gaussian Filter와의 비교

Template Matching by Correlation

• Video Link
• Cross Correlation을 maximize하면 그것이 template matching
• convolution과의 차이점은 flip이 없다는 것
• naive cross-correlation의 문제점은 output의 function의 value가 너무 크다는 것 --> normalize를 할 필요가 있다

convolution vs correlation	normalized cross-correlation

Image Processing 2

Overview

• Video Link
• 여전히 비슷한 목표를 가지고 있음
• Topics
  • (1) Fourier Transform
  • (2) Convolution Theorem
  • (3) Deconvolution in Frequency Domain
  • (4) Sampling Theory and Aliasing

Fourier Transform

• Video Link
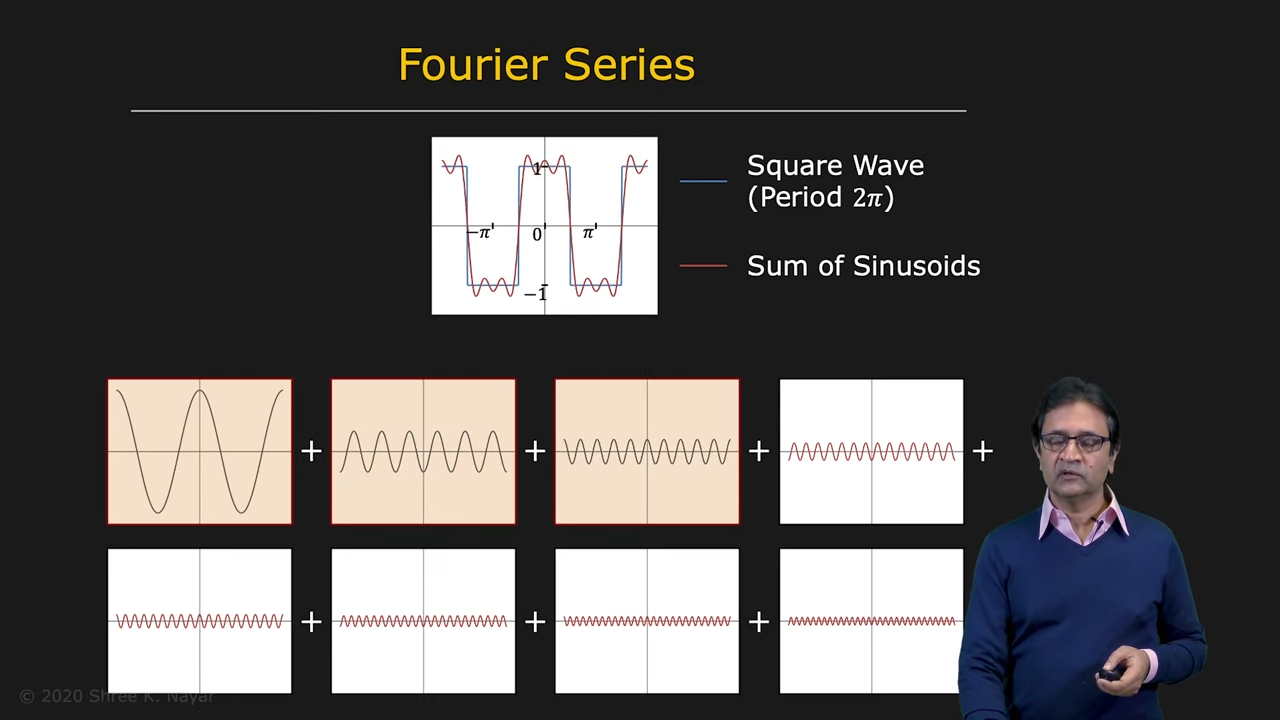
• 모든 Periodic Function은 서로 다른 frequency들을 가진 Infinite Sinusoidal들의 weighted sum으로 표현될 수 있다

sinusoidal이란?	finite fourier series의 예시

• fourier transform은 어떤 함수를 infinite fourier series로 변환하는 과정
• inverse fourier transform은 그 반대

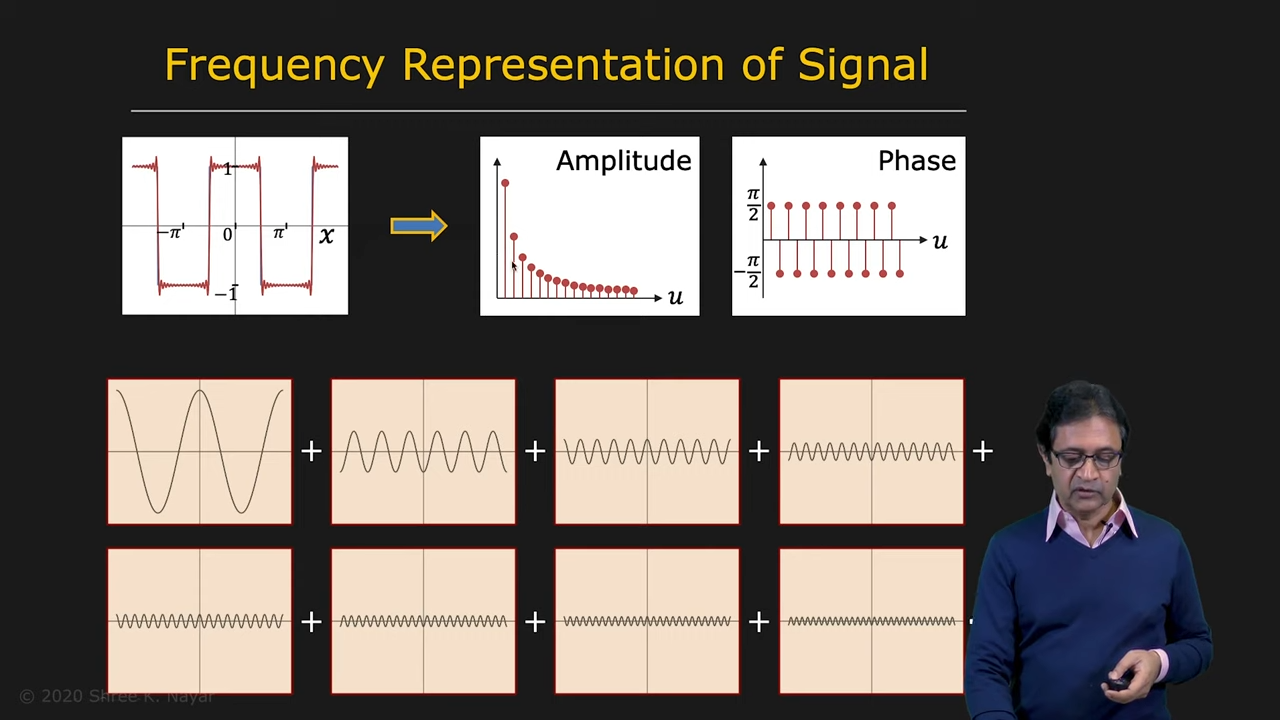목적은 어떤 함수를 amplitude와 phase로 쪼개는 것	FT와 IFT

• keyword : euler function, fourier transform
• example of fourier trasnform
  • cos -> delta function
  • sin -> delta function
  • delta function -> constant function
  • box filter -> sinc
  • gaussian function -> gaussian function

properties of fourier transform

Convolution Theorem

• Video Link
• Convolution은 Frequency Domain에서 더 효율적으로 계산될 수 있다

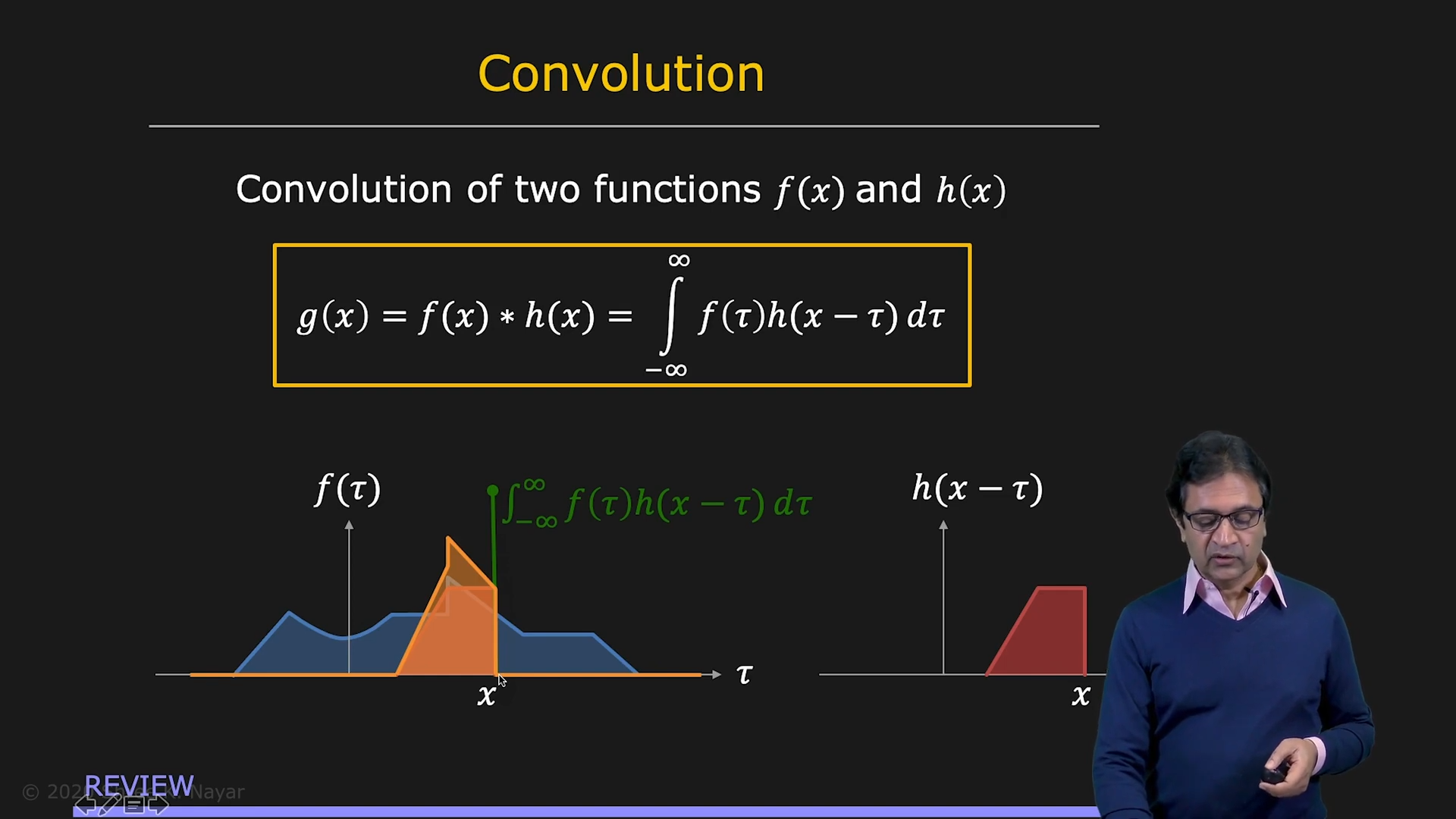Convolution의 정의	Fourier Transform과 Convolution

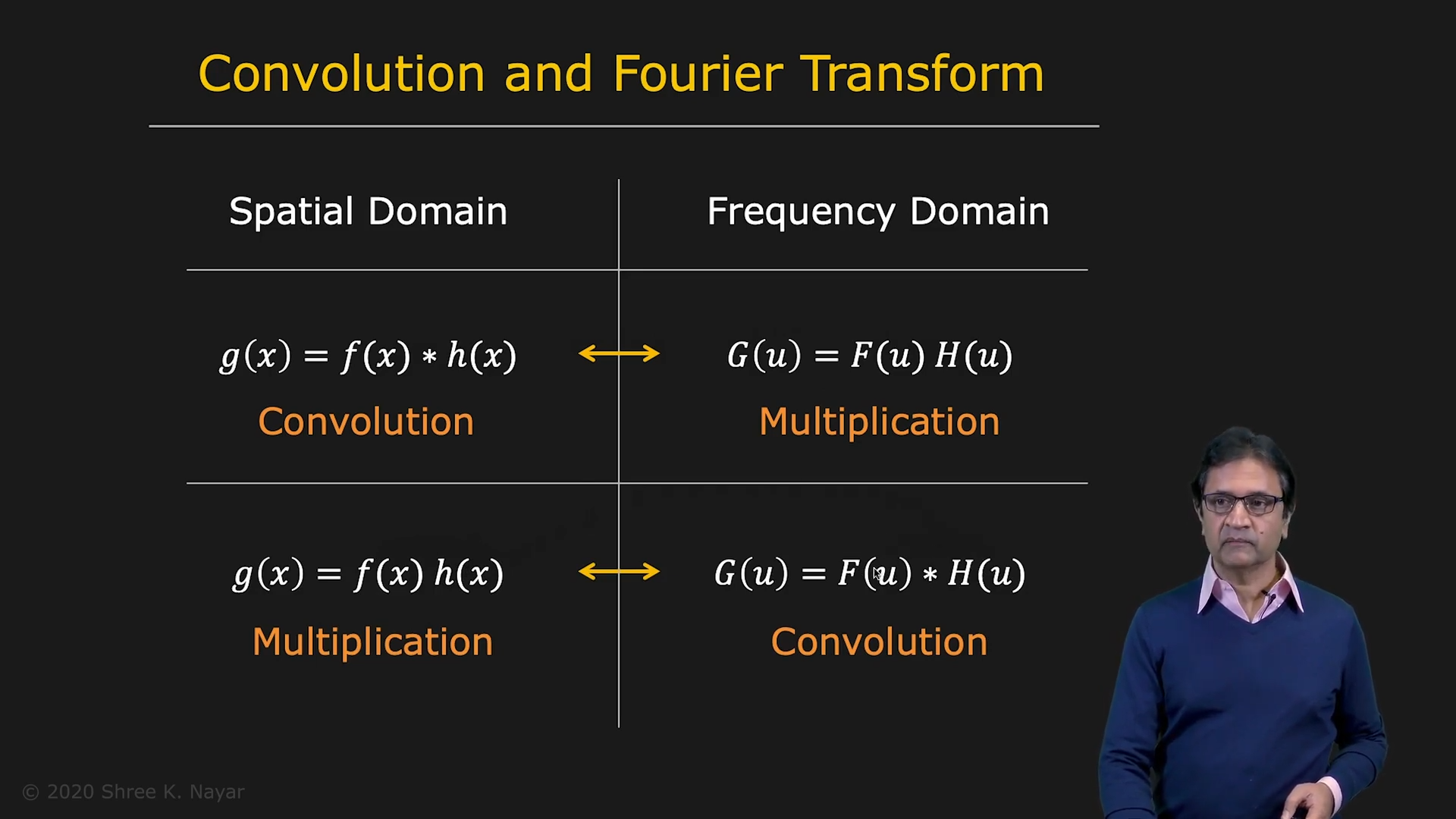각 도메인에서 multiplication과 convolution	Fourier Transform을 활용한 Convolution

• 예를 들면 gaussian smoothing은 fourier transform 후 low pass filter 후 inverse fourier transform을 이용해 더 효율적으로 계산될 수 있다

Image Filtering in Frequency Domain

• Video Link
• 이미지를 frequency domain에서 가지고 놀기 위해서는 Discrete Fourier Transform을 필요로 한다

DFT와 IDFT의 정의	x축은 주기, y축은 강도로 시각화 가능

• high-frequency가 많을수록 x축에서 다양하게 보여준다
• Noise는 마찬가지로 Noise가 된다

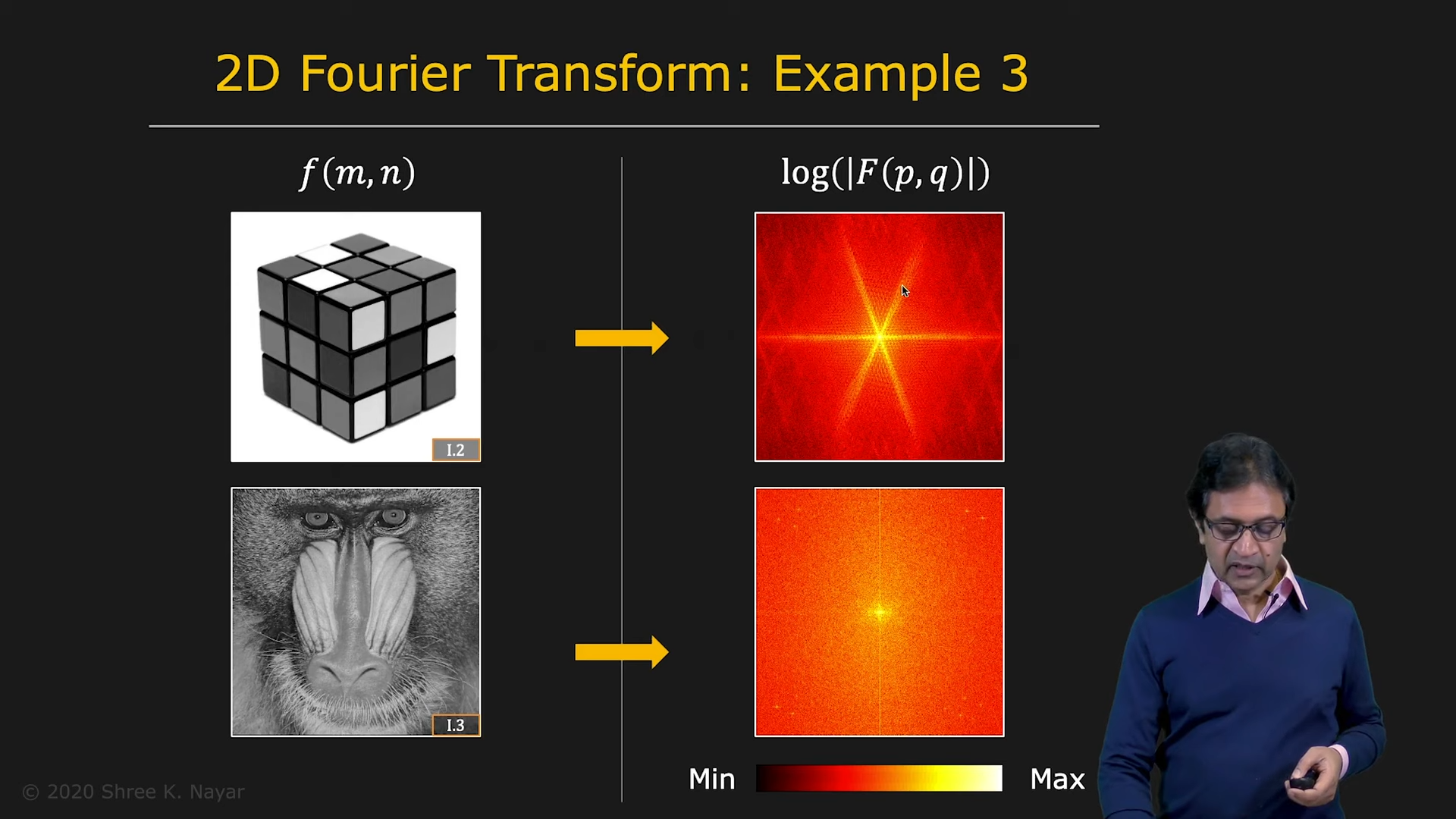Examples	Example

• Low-pass Filter를 통해 blur하게 만들고, High-pass Filter를 통해 edge와 같은 semantic한 정보를 찾아낼 수 있다

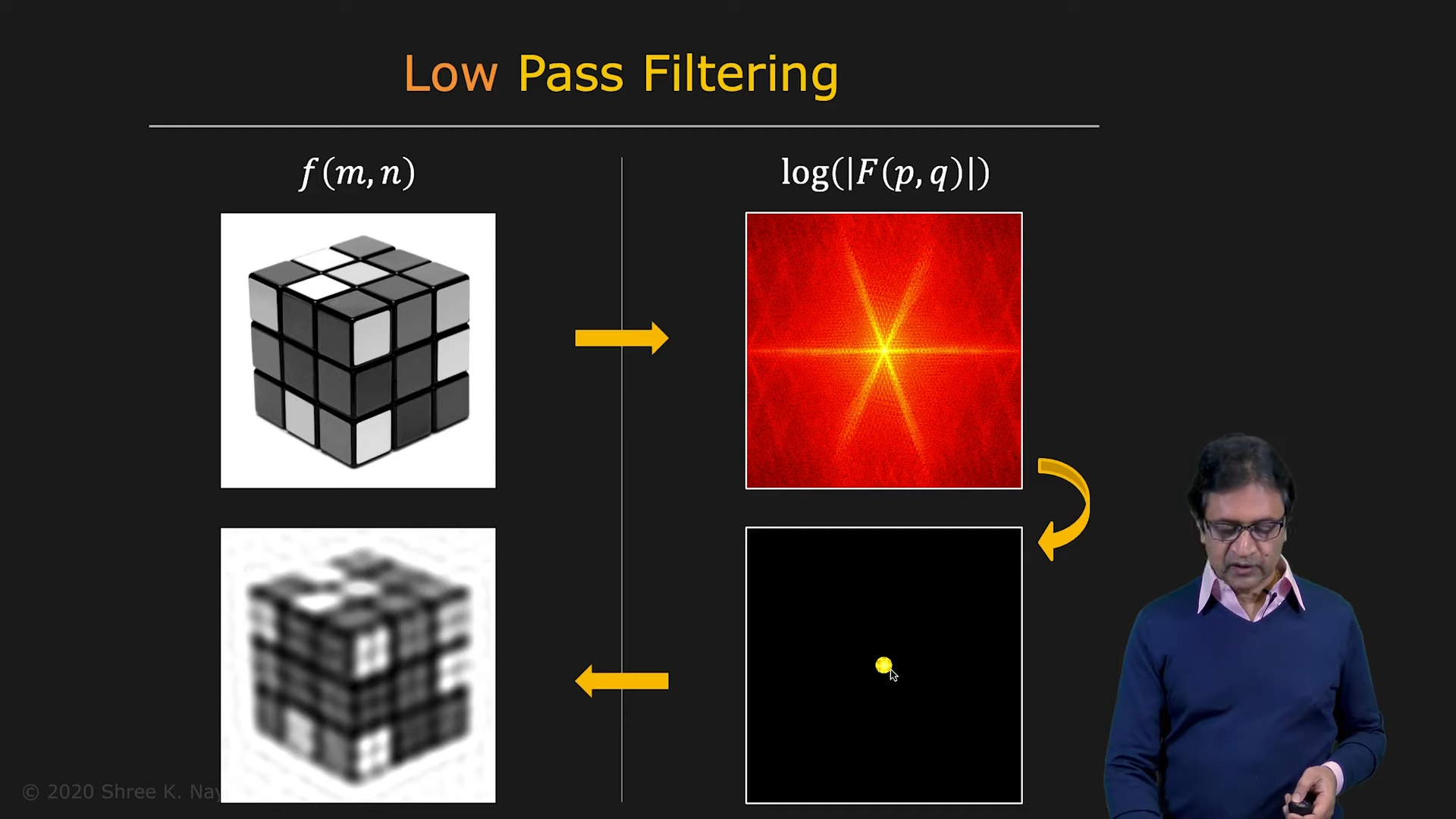Low-pass Filter	Low-pass Filter with smaller limit

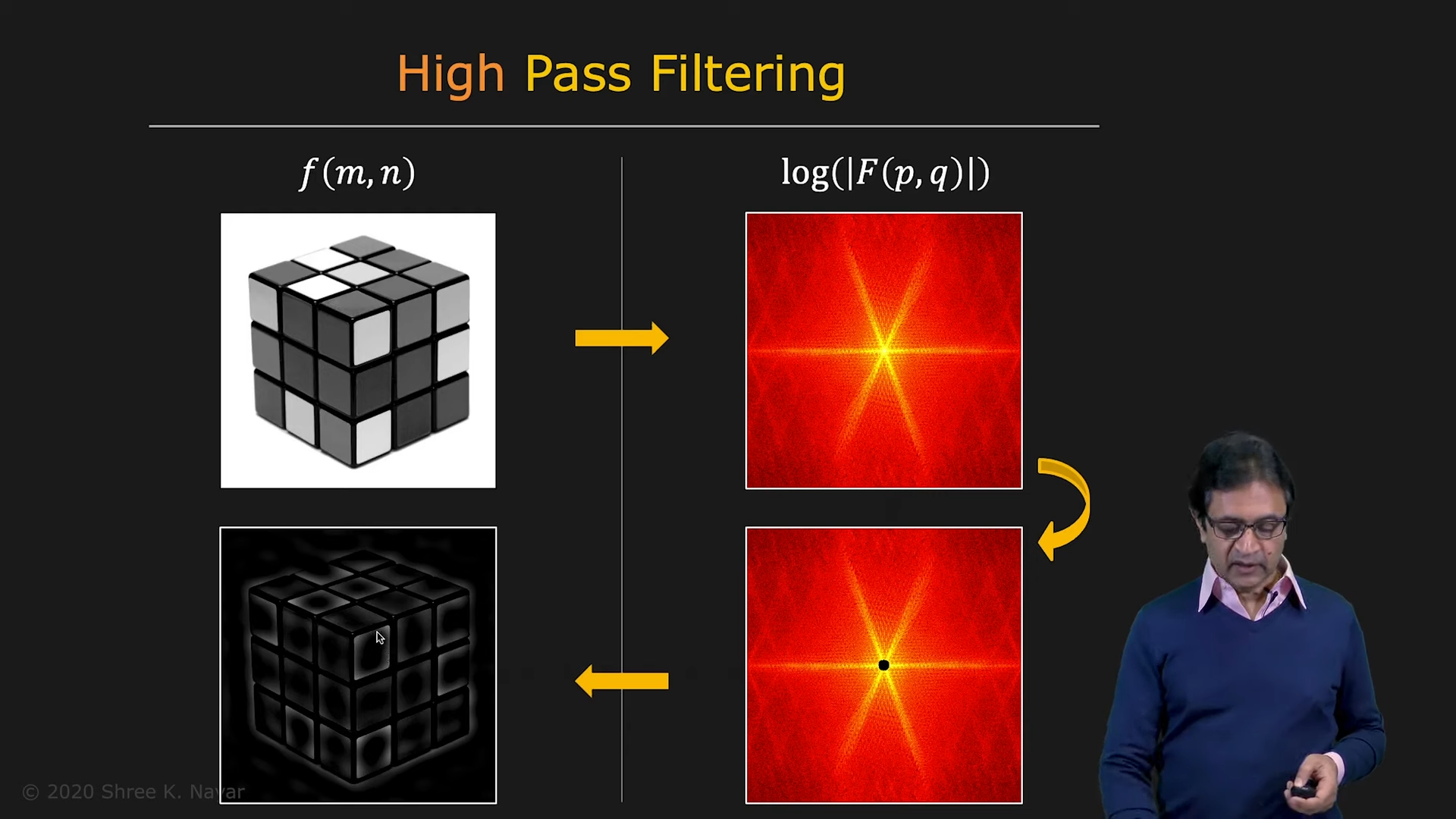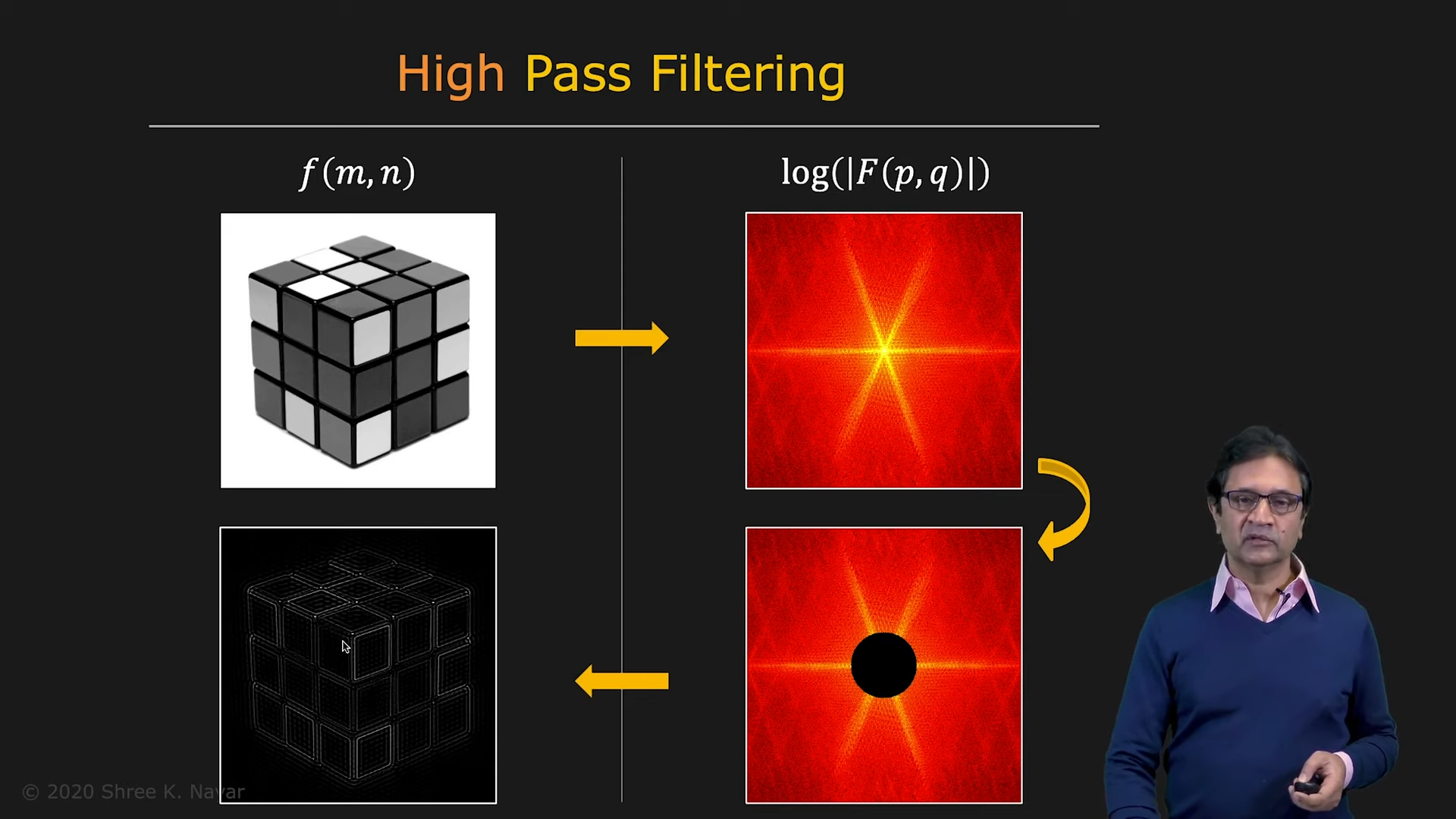High-pass Filter	High-pass Filter with larger limit

• multiplication을 통해 gaussian smoothing을 할수도 있다. (아까도 말했듯 이 방법이 더 빠를수도 있다)

frequency domain에서의 gaussian smoothing

• phase에 따라 가지고 있는 정보량이 다르다
• low freq info에서 대부분의 이미지 정보를 가져오고, high freq info에서 fine detail들을 가져오는 식으로도 응용이 가능하다

Phase(주기)가 더 많은 정보를 가지고 있다	이런 특성을 활용해 hybrid image도 만들 수 있다

Deconvolution

• Video Link
• Deconvolution을 통해서 convolution으로(LSIS하게) 가해졌을 거라고 추측되는 motion blur 등을 없앨 수 있다

convolution을 활용한 motion blur model	FT와 IFT를 이용한 해결 방향

• 문제는 motion blur 외에도 우리가 모르는 noise가 있을수도 있다는 것

가장 간단한 Noise Modeling	이 경우 그대로 기존의 방법론을 적용하면 결과는 좋지 않다

• motion blur보다 noise의 영향이 큰 곳에서는 우리의 방법론이 정상적으로 동작하지 않는다
• 이를 해결하기 위해 scaling을 통해 noise를 무시할 수 있도록 해야한다

왜 문제가 생기는가?	이를 해결하기 위한 방법

그런데 여기에는 hyper-parameter가 있다	적절한 값을 활용하면 우리가 원하는 수준을 얻을 수 있다

Sampling Theory and Aliasing

• Video Link
• continuous image plane은 object size를 전부 담아낼 수 없다. 이 경우 정보의 손실이 일어나거나 정보가 원하는대로 담기지 않을수도 있다.

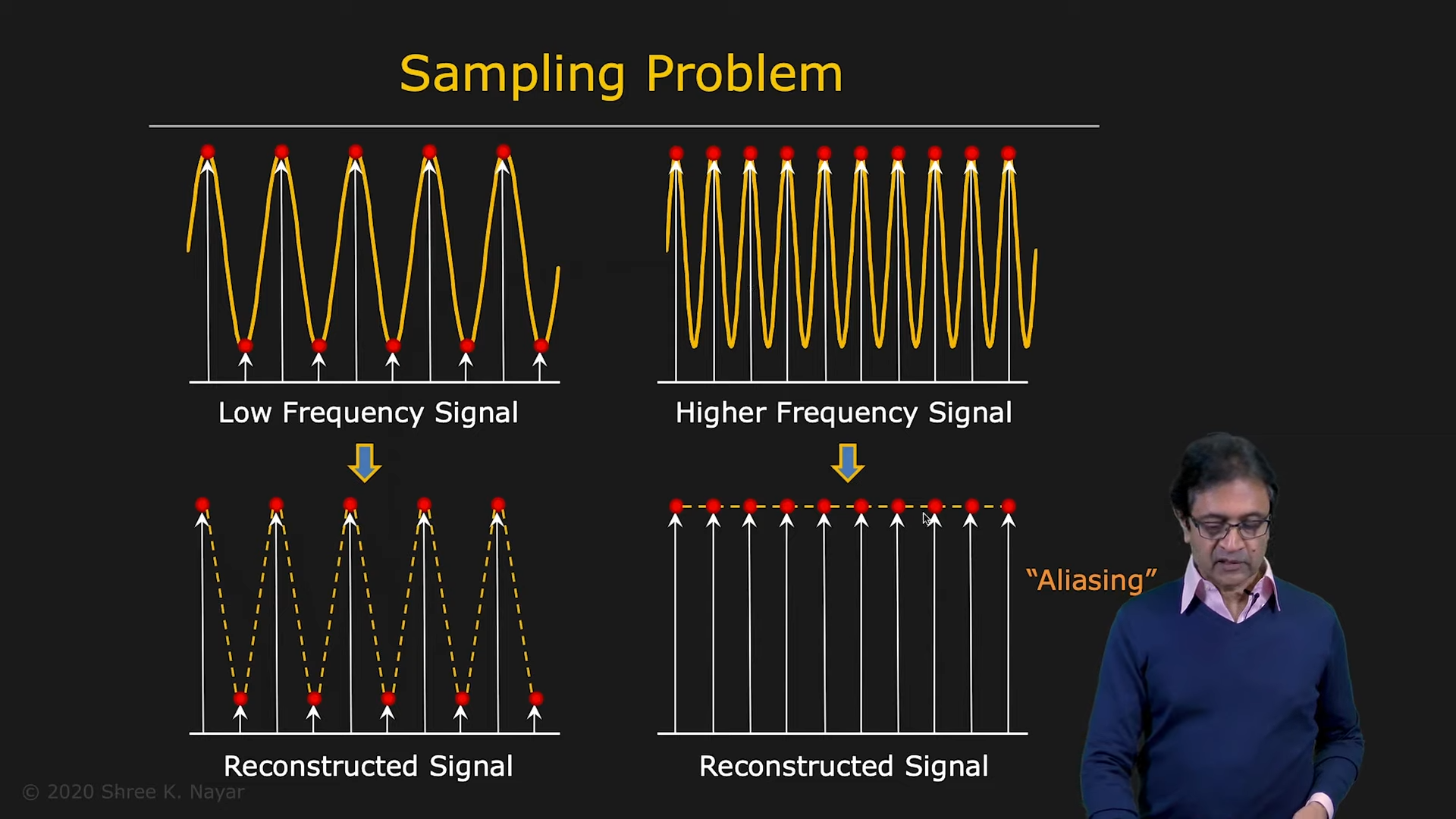aliasing이 일어나는 원인	aliasing의 예시

• 이를 해결하기 위해 우리는 sampling model을 생각해보고 어떻게 해결할 수 있을지 고민해볼 수 있다
• 아래 그림의 shah function (sum of delta functions)은 놀랍게도 fourier domain에서도 shah function이다. (대신 x축 scaling이 일어난다)

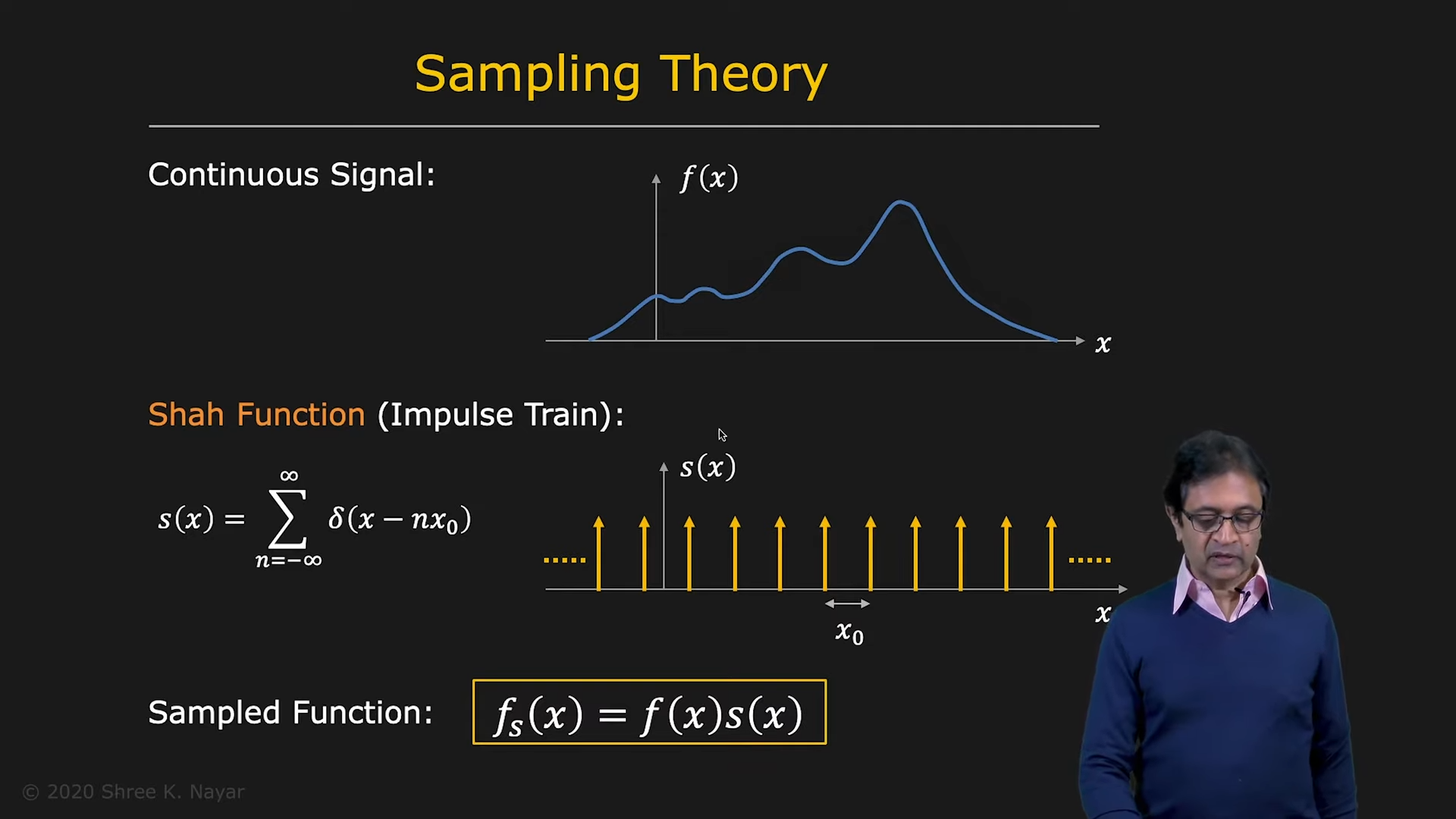sampling model	shah function의 fft 결과

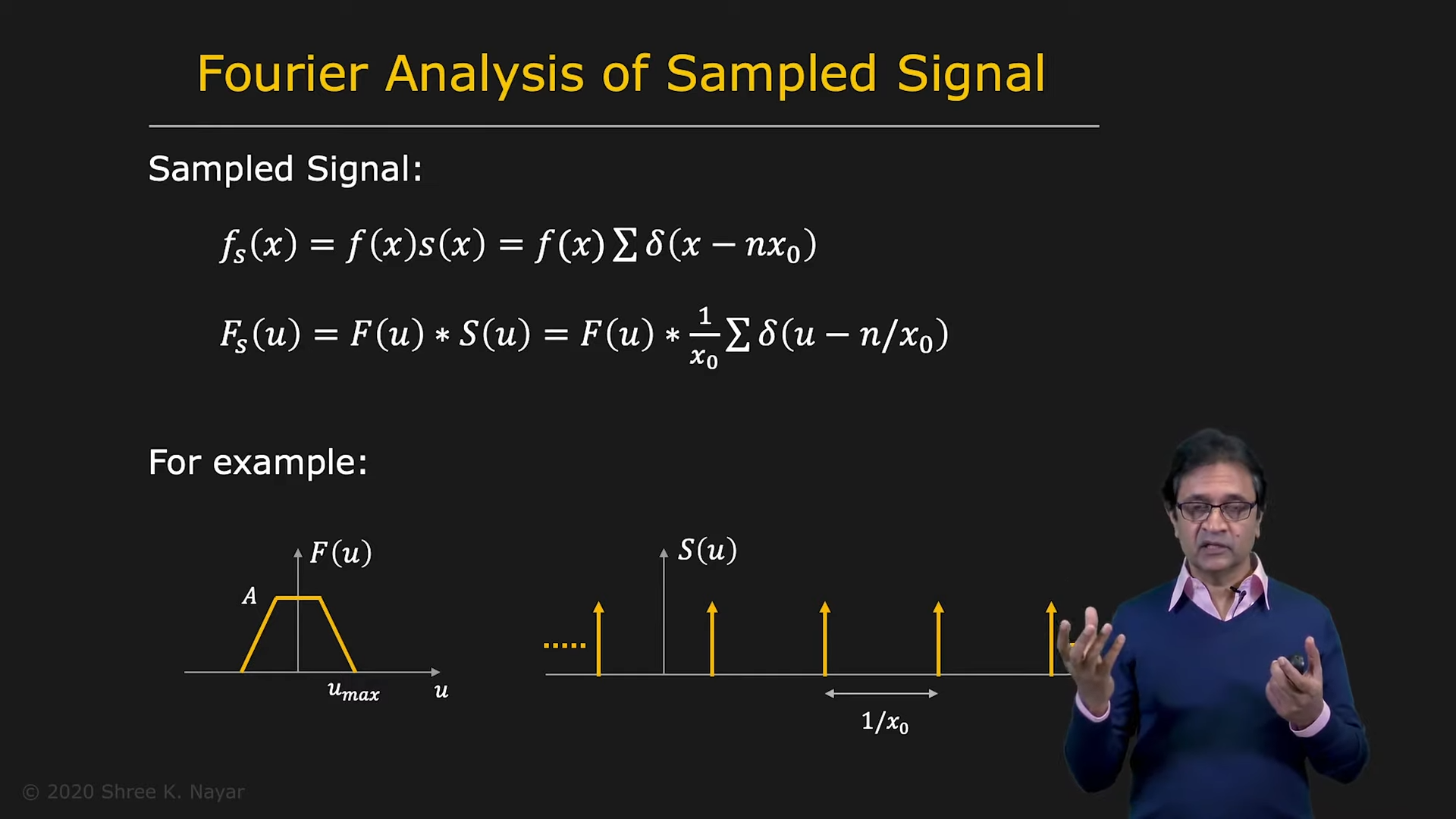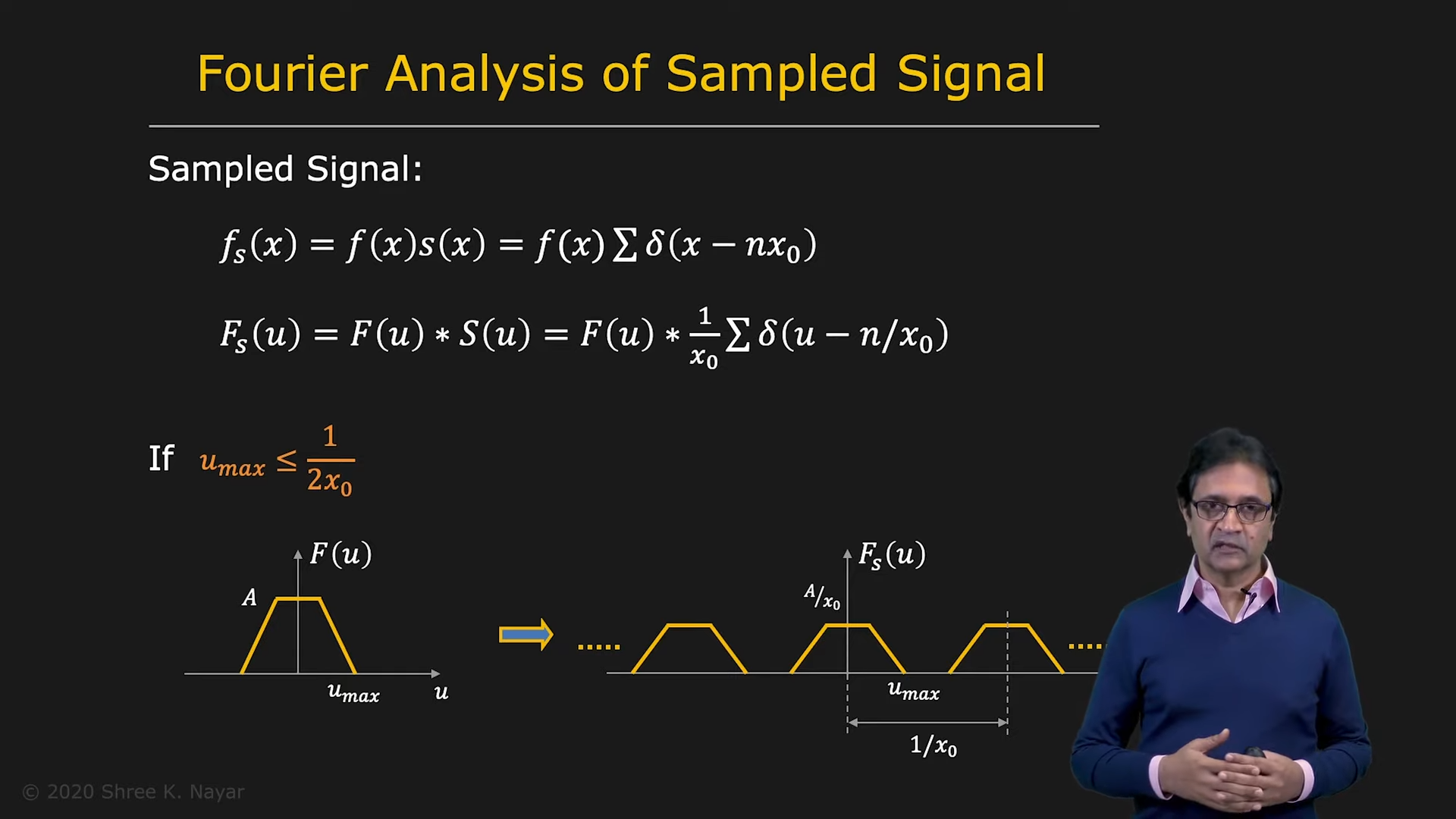shah function의 fourier analysis	보통 이렇게 겹치지 않을 때는 문제가 없다

이렇게 겹치면 문제가 된다	이렇게 발견한 현상은 어떻게 하면 이를 해결할 수 있는지에 대한 단서를 준다

이런 현상은 실제로 camera에 영향을 끼친다	그래서 이를 해결하기 위해 다음과 같은 해결책들을 사용한다