들어가기 전에
이 글은 무엇을 다루는가?
머신 러닝 분야의 탑 티어 컨퍼런스 중 하나인 ICLR 2019의 Best Paper Award를 수상한 The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks와 그 후속 연구들을 다룹니다.
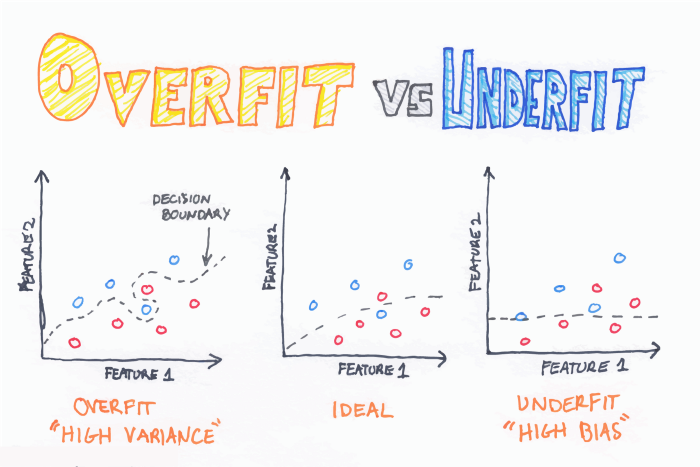
현재의 딥러닝 모델은 데이터의 수와 복잡성에 비해서도 훨씬 많은 파라미터를 사용하고 있습니다. 일반적으로 머신 러닝에서 the curse of dimensionality라는 이야기를 합니다. 요약하면 '더 많은 파라미터', '더 복잡한 모델'은 데이터의 수가 적을 경우 거의 암기해버리기 때문에 문제가 된다는 이야기인데요. 아래의 맨 왼쪽 그림처럼 과적합(Overfit)이 일어난다면 현재 주어진 학습 데이터는 정확하게 맞추지만 현실의 데이터는 바르게 추론할 수 없게됩니다. 중간지점이 가장 이상적이라고 할 수 있습니다.
 |
|---|
| 출처 : CURSE OF DIMENSIONALITY - Builtin |
하지만 딥뉴럴넷과 경사하강법(Gradient Descent)은 자체적으로 어느 정도 정규화(regularization) 효과가 존재하며, 그 결과 빅데이터와 딥러닝의 조합이 훌륭한 특징점 추출기(feature extractor)를 만드는 현존하는 최고의 방법(state-of-the-art)라는 것이 알려져 있습니다.
하지만 이 논문에서는 아래와 같은 가설을 제시합니다.
The Lottery Ticket Hypothesis. A randomly-initialized, dense neural network contains a subnetwork that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations.
번역하면 다음과 같습니다.
무작위로 초기화된 밀집된 딥뉴럴넷에서 어떤 부분을 가져왔을 때, 따로 트레이닝 하더라도, 기존의 네트워크와 같은 성능을 같은 학습 횟수 내에 달성할 수 있을 것이다.
이게 무슨 이야기일까요? 일반적으로 딥뉴럴넷의 트레이닝에는 비싼 GPU를 많이 필요로 합니다.
 |
|---|
| GPU Memory를 마지막 한톨까지 뽑아먹고 있는 랩메이트 |
그런데 아래와 같이 기존의 밀집된 네트워크에서 부분을 가져와서 학습을 시킬 수 있다면 훨씬 GPU를 적게 쓰면서도 학습 속도도 빨라질 것입니다. 그러나 모델의 크기가 줄어들면 학습할 수 있는 양도 줄어들기 때문에 당연히 성능이 떨어지기 마련입니다.
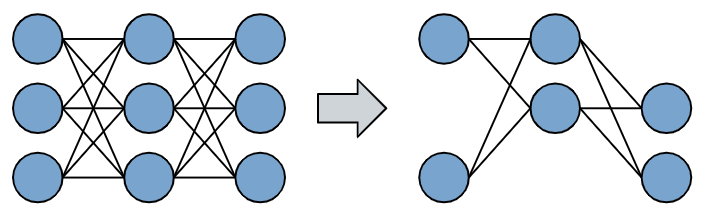
하지만 이 논문에서는 오른쪽과 같이 부분적인 네트워크를 잘 골라내면 기존의 큰 네트워크와 같은 효과를 낼 수 있을 거라고 생각했는데 그게 바로 Lottry Ticket Hypothesis입니다.
그리고 이 논문에서는 그 방법중에 하나로 (대단히 비효율적인)Iterative Manitude Pruning을 통해 부분 네트워크를 잘 찾는 방법을 제안합니다. 그리고 이 논문에 영감을 받은 많은 연구자들이 효율적으로 잘 찾는 방법을 많이 제시하는데 그게 이 글의 주제입니다.
어떤 기반 지식이 필요한가?
이 글은 어느 정도 컴퓨터 비전에서 사용되는 딥러닝에 익숙하다는 전제하에 쓰여진 글입니다. ResNet으로 이미지 분류(Image Classification) 문제를 해결하는 방법을 알고 있다면 굉장히 좋습니다. 아래와 같은 단어들에 익숙하다면 더욱 좋습니다.
- Deep Neural Network
- Convolution Layer
- Back-propagation, Gradient Descent
- MNIST, CIFAR10, ImageNet
논문의 내용
Iterative Magnitude Pruning
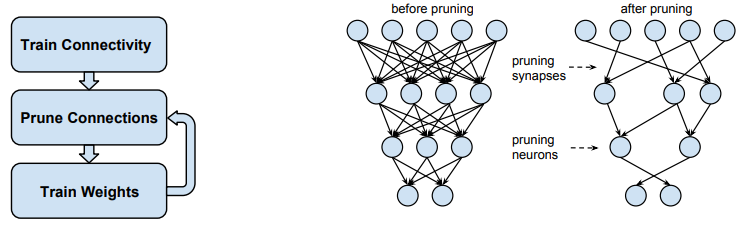
이 논문을 이해하기 위해서는 우선 Network Pruning에 대해서 알고 있어야합니다. Network Pruning은 아래와 같이 어떤 네트워크가 있을 때 어떤 기준을 가지고 중요하지 않은 뉴런(노드)과 시냅스(연결)을 제거하는 기법을 의미합니다.
일반적으로 학습된 네트워크에서 가중치의 크기(magnitude)가 작은 뉴런을 제거하고 가지치기된 네트워크를 가지고 다시 학습시키는 방식을 사용합니다. 왜냐하면 가중치가 작은 연결의 결과물은 최종 결과물에 적게 반영되고 덜 중요하다는 뜻이니까요. 뇌에서 활성화되지 않는 뉴런들이 점차 사멸하는 것을 생각하면 이해하기가 더 쉽습니다.
이러한 과정을 반복적으로 수행하는 것을 Iterative magnitude pruning이라고 합니다.
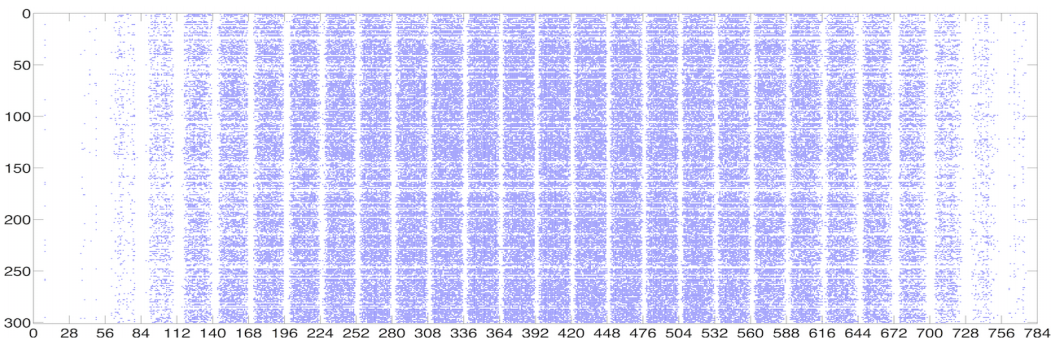
이런 방식의 모델 압축이 가능한 이유는 딥뉴럴넷의 모델이 가지고 있는 레이어를 시각화하면 아래와 같이 희미한(Sparse) 구조가 나타나기 때문입니다. 즉 중요한 뉴런은 생각보다 많지 않기 때문에 최대 90%의 압축을 해도 성능은 겨우 1~2% 정도가 떨어지는 현상이 나타나게 됩니다.
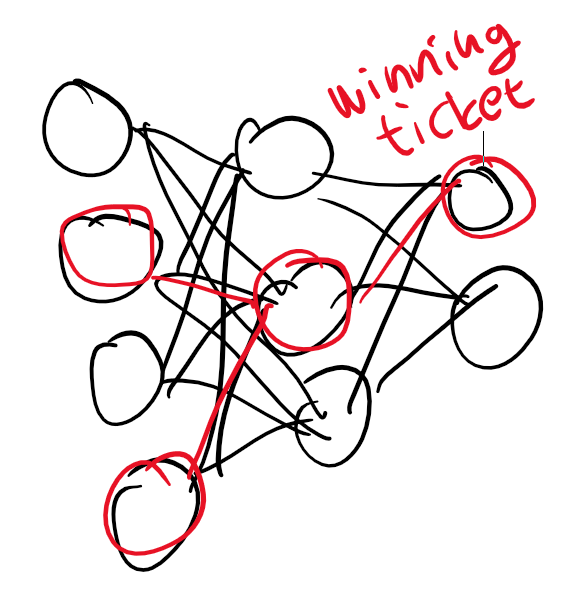
당첨 복권(winning ticket) 찾기
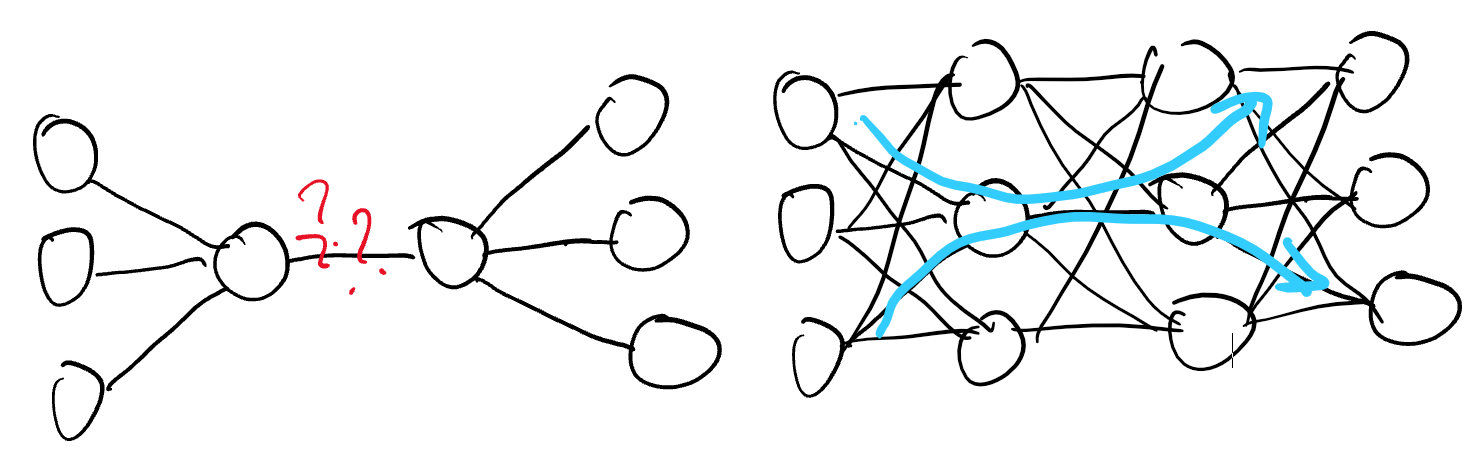
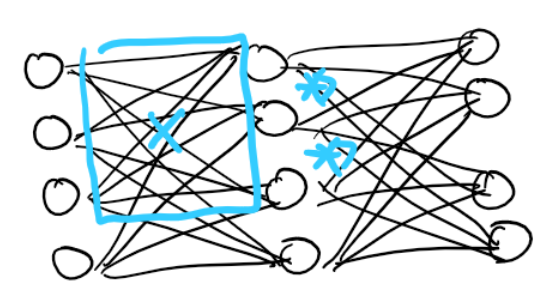
그러면 여기에서 궁금해집니다. 어차피 가지치기를 한 뒤에 학습을 다시 시켜야한다면 가지치기를 먼저하는 방법은 없을까? 실제로 많은 연구자들이 시도했지만 경험적으로 불가능함을 알게됩니다.
좌측 그림처럼 우리는 빨간 뉴런만 학습시키고 싶어도 우측 그림처럼 이웃 뉴런들이 있어야 바르게 학습이 되었던 것입니다. 게다가 가지치기 이후에는 이미 빨간 뉴런의 값이 한쪽으로 쏠려있어서 fine-tuning을 하기가 쉽지 않았습니다.
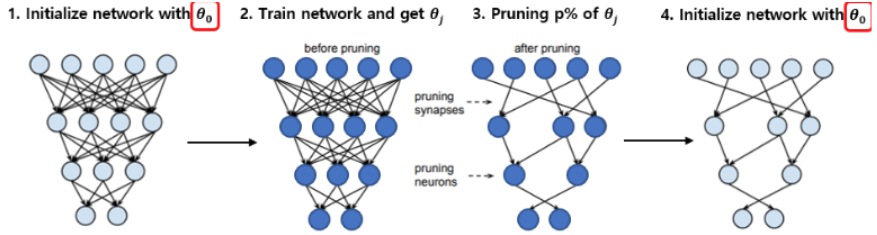
이 논문에서는 이러한 문제를 reinit이라는 기법을 통해서 이를 해결합니다. 중요한 뉴런이 무엇인지 저장된 마스크(mask)는 학습 된 네트워크를 기준으로 가져오되, 가중치는 학습하기 전의 네트워크에서 가져오면(reinit) fine-tuning이 가능했습니다.
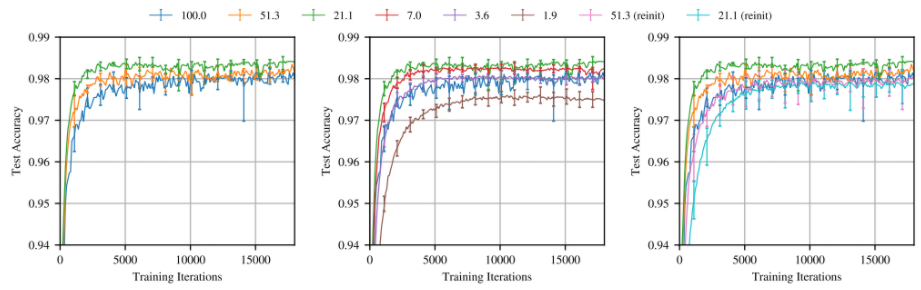
실제로 이렇게 찾아낸 작은 네트워크는 기존의 네트워크보다 같거나 더 좋은 성능을 같은 학습 반복(training iteration) 내에 달성하게 됩니다.
연구의 한계점
그런데 뭔가 이상하지 않나요? 마스크를 학습된 네트워크 기준으로 가져온다니? 결국 이 논문에서 제시한 방법론은 학습 전 가지치기를 위해, 학습을 필요로 하게 됩니다. 전혀 현실적으로 쓸 수 없는 방법론을 제시한거죠.

다만 이러한 당첨 복권(winning ticket)의 존재를 알렸다는 점에서 이 연구는 큰 의의가 있었으며 많은 후속 연구들이 학습 없이도 적절한 mask를 찾기 위한 연구에 돌입하게 됩니다.
후속 연구
다른 모델, 학습기, 과제, 데이터셋에서도 동작하는가?
The Lottery Ticket Hypothesis에서는 vgg, resnet과 같은 모델, SGD(Stocastic Gradient Descent)라는 학습기(optimizer), 이미지 분류(Image Classification)이라는 과제(task), CIFAR10이라는 데이터셋을 이용해 실험을 진행했습니다. 그런데 당첨 복권(winning ticket)이 다른 곳에도 다 존재하는 걸까요?
이를 검증하기 위해 아래와 같은 연구들이 진행됩니다.
- One ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers
- Winning Ticket이 Fashtion MNIST, SVHN, CIFAR-10/100, ImageNet, Places365등의 다양한 데이터셋에서 찾아진다는 것을 증명했습니다.
- 또한 SGD뿐 아니라 Adam에서도 동작한다는 것을 증명했습니다.
- Playing the lottery with rewards and multiple languages: lottery tickets in RL and NLP
- 강화 학습(reinforcement learning)과 자연어 처리(natural language processing)에서도 lottery ticket 현상이 나타난다는 것을 증명합니다.
어떻게 하면 학습을 덜 하거나 안 하고 당첨될 수 있는가?
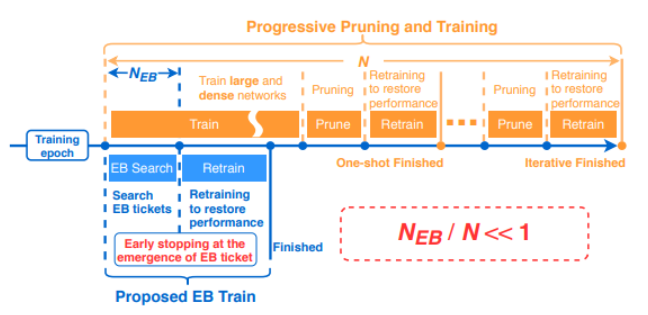
- DRAWING EARLY-BIRD TICKETS: TOWARDS MORE EFFICIENT TRAINING OF DEEP NETWORKS
- 학습을 끝까지 시킬 필요 없이 큰 learning rate로 조금만 학습시키고 mask를 가져와도 winning ticket을 찾을 수 있다는 내용입니다.
- SNIP: SINGLE-SHOT NETWORK PRUNING BASED ON CONNECTION SENSITIVITY
- 데이터를 전체 다 볼 필요 없이 한번씩만 보고 mask를 가져와도 된다는 내용입니다.
- PICKING WINNING TICKETS BEFORE TRAINING BY PRESERVING GRADIENT FLOW
- weight 말고도 gradient를 보면 더 정확한 mask를 가져올 수 있다는 내용입니다.
- Pruning neural networks without any data by iteratively conserving synaptic flow
- 데이터를 안 보고도 처음부터 중요한 뉴런들을 찾을 수 있다는 내용입니다.
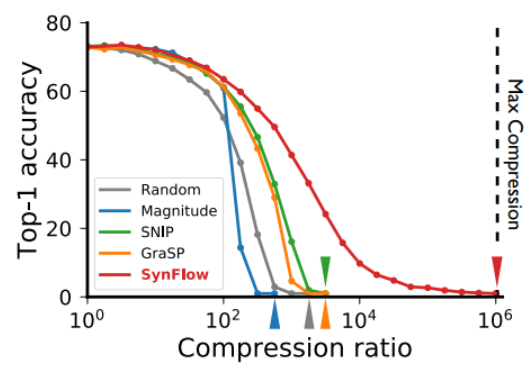
왜 데이터를 보지도 않고 딥뉴럴넷에서 중요한 뉴런들을 찾아낼 수 있는가?
제가 Lottery Ticket 계열의 연구를 좋아하는 이유 중 하나는 Network Pruning이라는 기법을 통해서 딥뉴럴넷이 무엇이 중요하다고 학습하는지를 알 수 있고 이를 통해 딥뉴럴넷을 더 깊게 이해할 수 있기 때문입니다.
실제로 위와 같이 데이터를 보지 않고도 중요한 뉴런이 무엇인지 알아나가는 과정에서 우리는 딥뉴럴넷이 무엇을 학습하고 있는지, 왜 어떤 뉴런은 초기화되자마자 중요하고 중요하지 않은지를 알 수 있습니다.
딥뉴럴넷이 초기 학습에서 배우는 것
마치 태아나 신생아의 초기 발달 과정에서 중요 학습 기간(critical learning period)가 있는 것처럼 딥뉴럴넷도 학습의 초기에 현재 나에게 있는 뉴런과 시냅스 중 어느 것이 중요한지 등을 판단한다고 합니다. 그래서 아래와 같이 초기에 이상한 데이터를 학습시키면 상당한 정확도 손실이 있는 반면, 초기를 지나고 나면 안정적으로 학습을 하게됩니다.
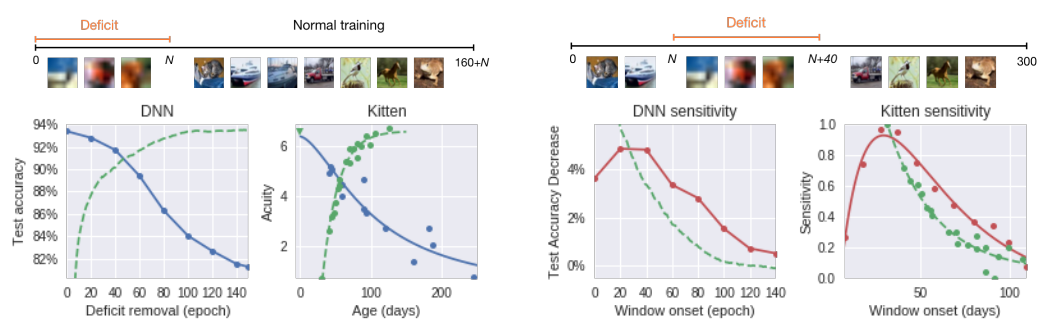
특히 컴퓨터 비전 문제에 사용되는 CNN(Convolution Neural Network)의 경우에는 학습 초기 형태와 같은 정보들을 학습하고 나중에는 점점 더 디테일한 부분들을 학습하게 됩니다.
레이어 붕괴(Layer Collapse)
마지막에 데이터를 안 보고도 처음부터 중요한 뉴런을 찾을 수 있다고 주장한 논문에서 제시한 문제점입니다. 가지치기를 할 때 문제가 되는 것 중 하나는 아래와 같이 앞에서 길이 끊어져버리면 뒤에 있는 중요한 뉴런들이 정보를 받지 못 하게 되고 이로 인해 학습 자체가 불가능하게 되는 것입니다.
그래서 이러한 문제만 방지할 수 있으면 이론상으로 압축가능한 최대치를 달성할 수 있다는 게 이 논문의 주장이죠!
결론
Lottery Ticket Hypothesis는 딥뉴럴넷의 트레이닝에 필수적이라고 믿어왔던 것들이 실제로는 그렇지 않다는 것을 보여주고 있습니다. 이 가설이 맨처음 나왔을 때는 당첨 티켓(winning ticket)을 찾는 일이 Iterative Magnitude Pruning과 같이 값비싼 방법론을 필요로 했습니다. 하지만 여러 연구자들의 협업을 통해서 특정 상황에서는 심지어 데이터를 보지 않고도 학습 가능한 작은 네트워크를 찾을 수 있었습니다.
많은 기술들의 발전 과정과 굉장히 비슷한 것 같습니다. 처음에는 많은 자원과 시간을 소모해서라도 '이게 되네?'라는 걸 보여줍니다. 지금까지의 딥러닝 모델들도 그러했듯이요.

하지만 그런 기술들이 실생활에서 응용되려면 효율적이고 안정적일 필요가 있습니다. Lottery Ticket Hypothesis는 스스로의 발전과정도 그러하지만 딥러닝이라는 기술이 산업계에서 더 잘 응용되기 위한 기술인 것 같습니다.

The Lottery Ticket Hypothesis suggests that within large neural networks, smaller sub-networks can achieve similar performance—much like how a single winning lottery ticket stands out. Platforms like PejuangJitu capitalize on this idea of rare success, blending chance and strategy. Learn more at https://hillviewavionics.com/