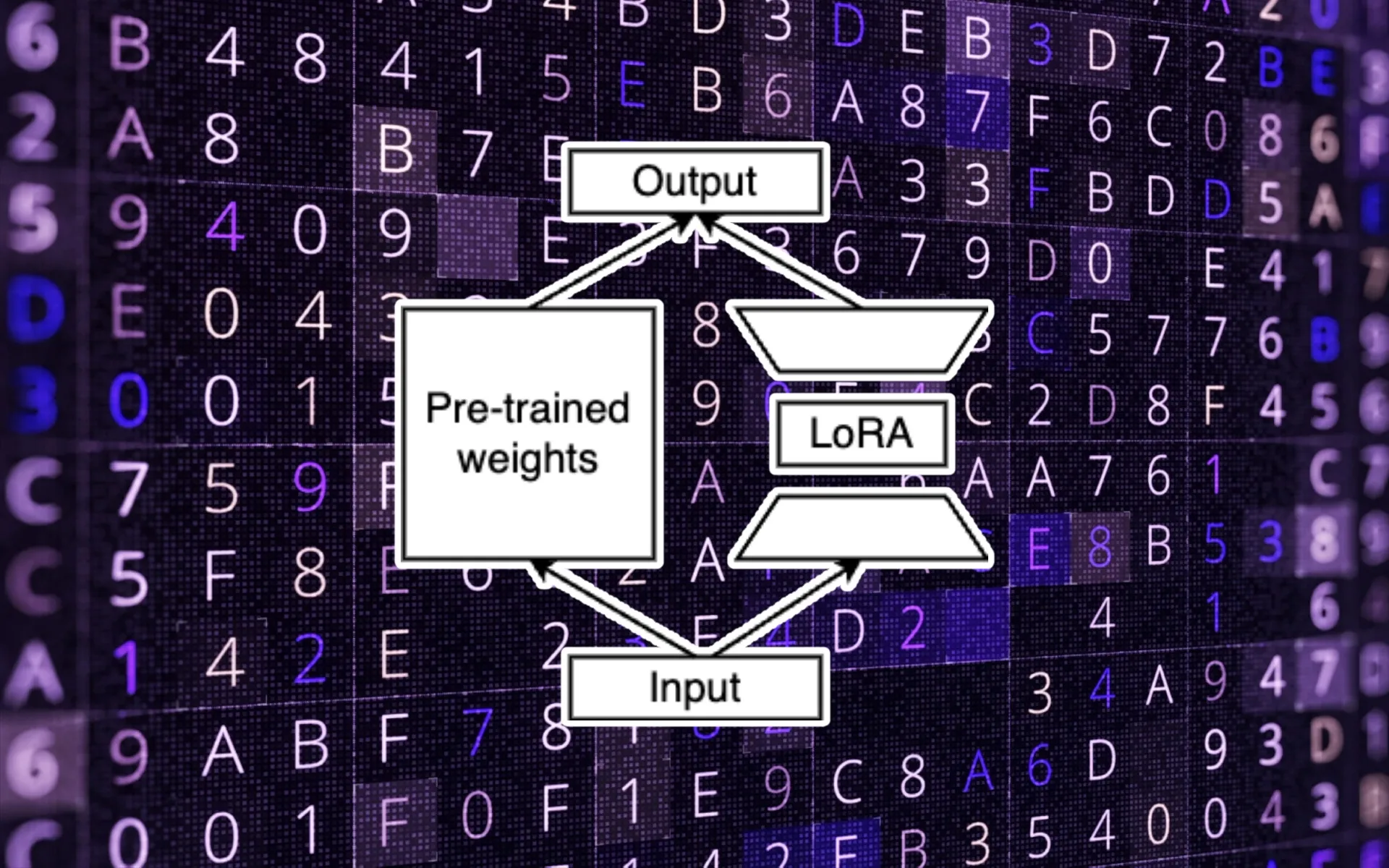
LoRA 발표소개

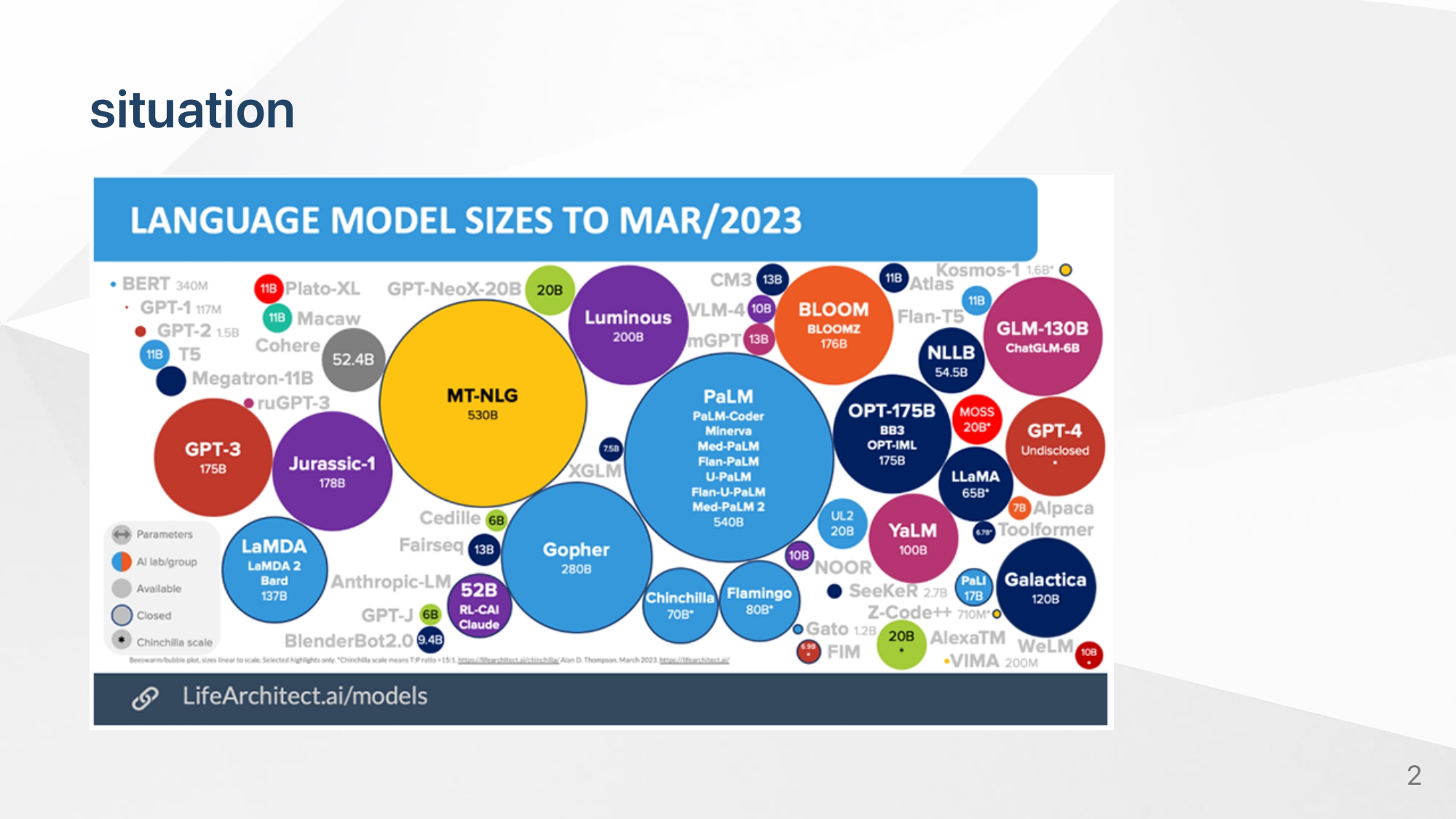
위와 같은 large pretrained 모델들이 대두하고 있는 상황에서 , downstream task에 효율적으로 finetuning하는 방법론은 매우 중요해지고 있다.



만약에 위처럼 objective function이 이루어지면, GPT-3 같은 경우 175B의 모든 파라미터가 업데이트해야한다. 하지만, 현실적으로 전 세계 극소수 기업들을 제외하고는 불가능하다. 그 전에 backward 과정에서 optimizer에 따라서 차지하는 VRAM이 다름을 아래처럼 나타내 보았다.
Optimizer state
SGD

Adam

adam같은 경우에는 optimizer state가 존재하기 때문에 SGD보다 더 큰 VRAM을 차지하게된다.
Inspiration

이러한 상황속에서 몇개의 논문이 나오는데, LLM같은 over-parameterized model은 실제로 low intrinsic dimension으로 표현 가능하다는것.

LoRA Concept

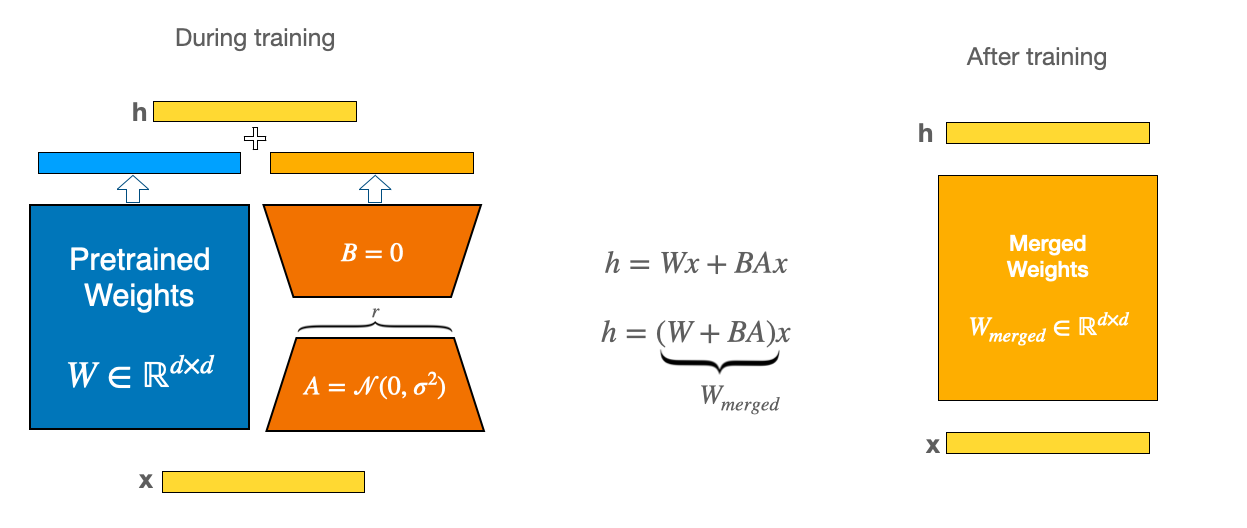

fully-finetuning과 LoRA의 objective function을 보면 식은 비슷하지만, trainable한 파라미터가 다르다. pretrained weights는 freeze한 상태로, attention weights를 low rank decomposition해서 A,B로 만들어 concat한다. 결국 A,B만 학습시킨다. 여기서 이점은 rank의 크기가 d에 비해 매우 작기때문에 trainable한 파라미터수가 매우 작아진다.
what is Rank?
선형대수에서 말하는 rank의 개념을 간단하게 소개한다.
만약에 Linear map : 라고 할때,
정의 : row-reduced echelon form에서 1의 개수 = -
여기서 는 matrix 에 대응한다.


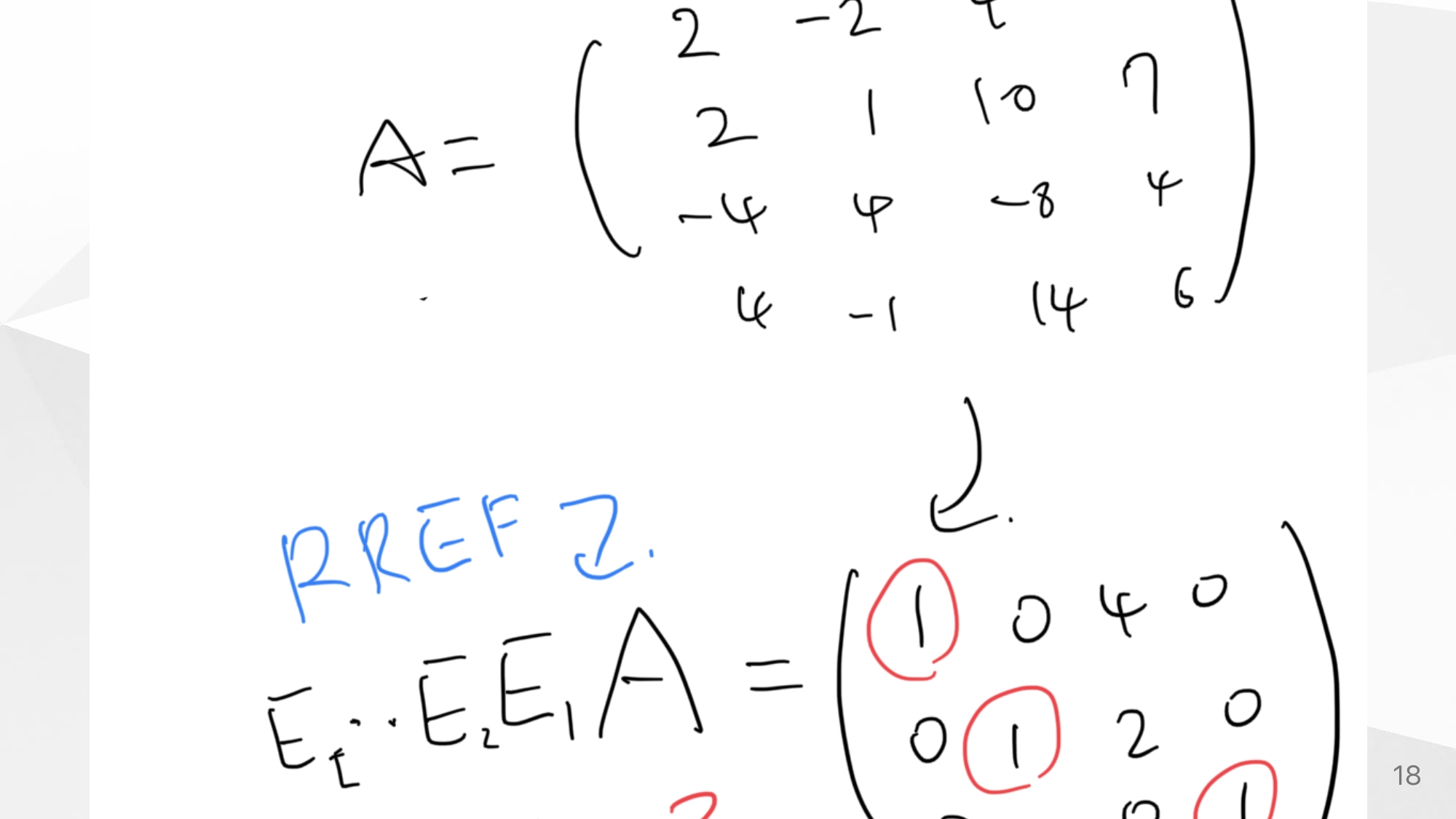



LoRA말고 다른 방법들도 보면 좋다.
CODE
microsoft의 공식 문서에서 코드를 살펴보자.
https://github.com/microsoft/LoRA
A,B Definition
class Linear(nn.Linear, LoRALayer):
# LoRA implemented in a dense layer
# Actual trainable parameters
if r > 0:
self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
self.scaling = self.lora_alpha / self.r
# Freezing the pre-trained weight matrix
self.weight.requires_grad = False
self.reset_parameters()
if fan_in_fan_out:
self.weight.data = self.weight.data.transpose(0, 1)
A,B initalize
type1
def reset_parameters(self):
self.conv.reset_parameters()
if hasattr(self, 'lora_A'):
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.kaiming_uniform_(self.lora_A, a=math.sqrt(5))
nn.init.zeros_(self.lora_B)type2
# LoRA implemented in a dense layer
def reset_parameters(self):
nn.Embedding.reset_parameters(self)
if hasattr(self, 'lora_A'):
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.zeros_(self.lora_A)
nn.init.normal_(self.lora_B)
elementwise sum
def train(self, mode: bool = True):
def T(w):
return w.transpose(0, 1) if self.fan_in_fan_out else w
nn.Linear.train(self, mode)
if mode:
if self.merge_weights and self.merged:
# Make sure that the weights are not merged
if self.r > 0:
self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
self.merged = False
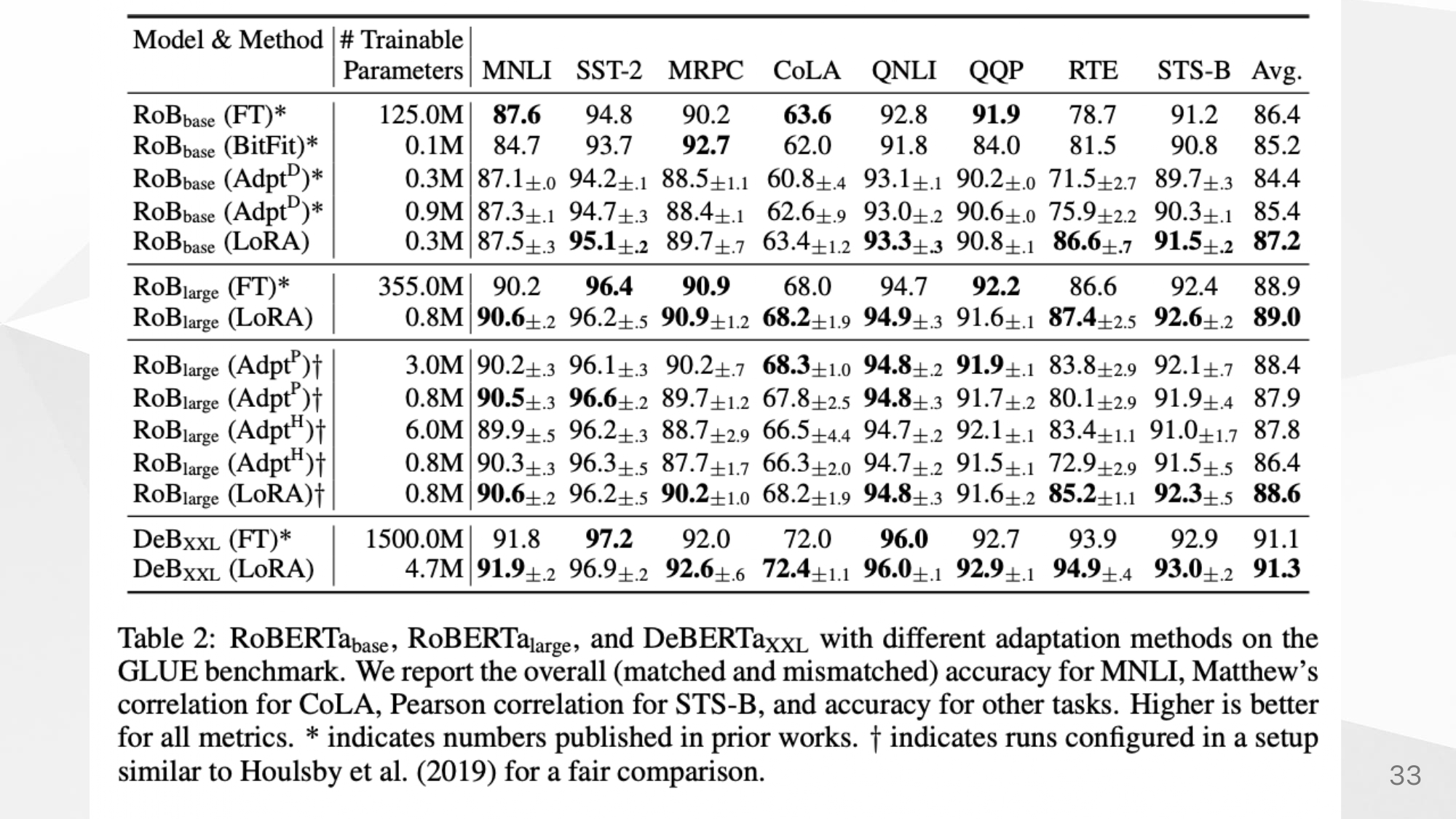
Experiments
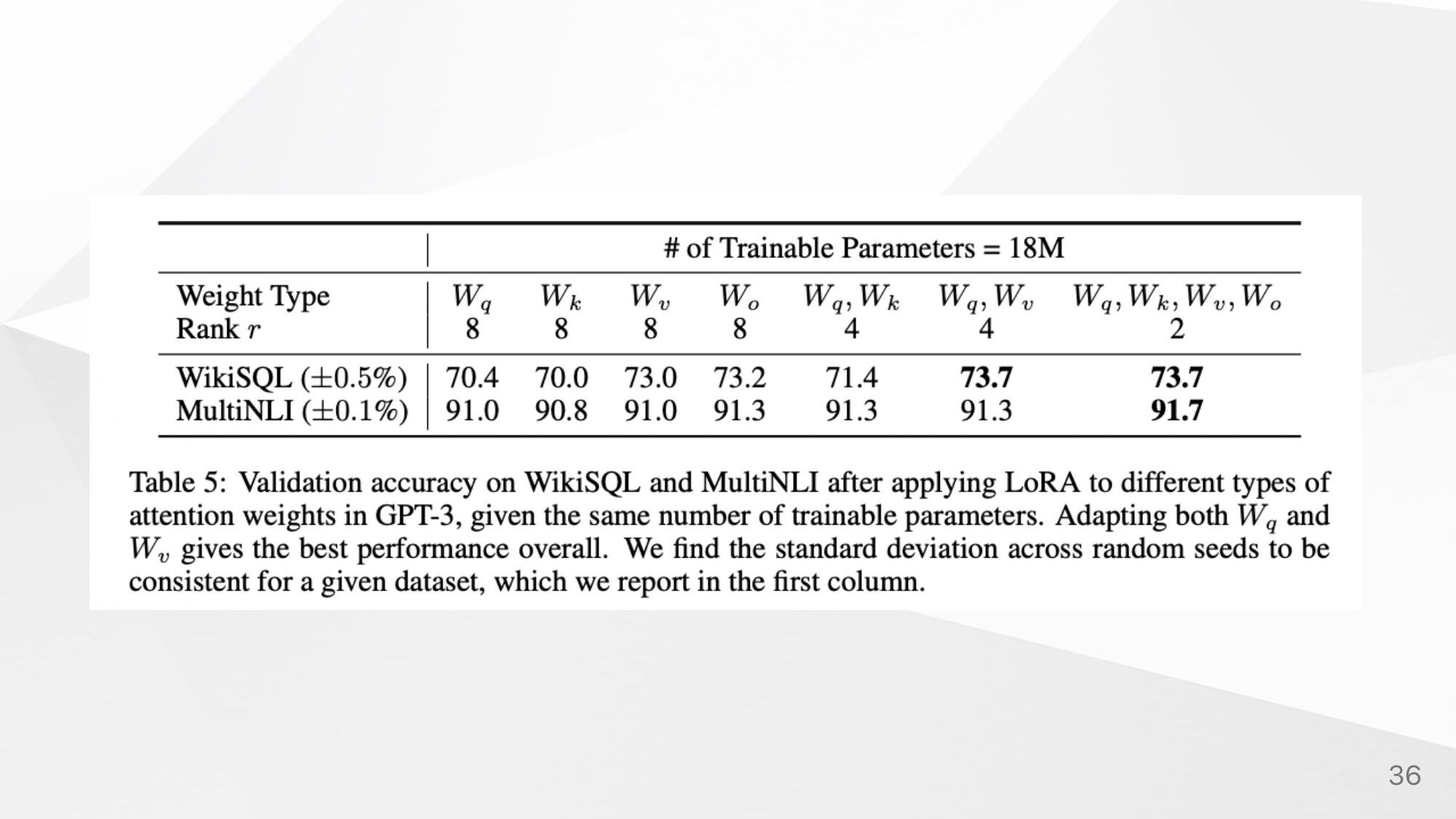
LoRA말고도 Adapter와 prefix, fully-finetuning에 대해 성능을 비교했다.
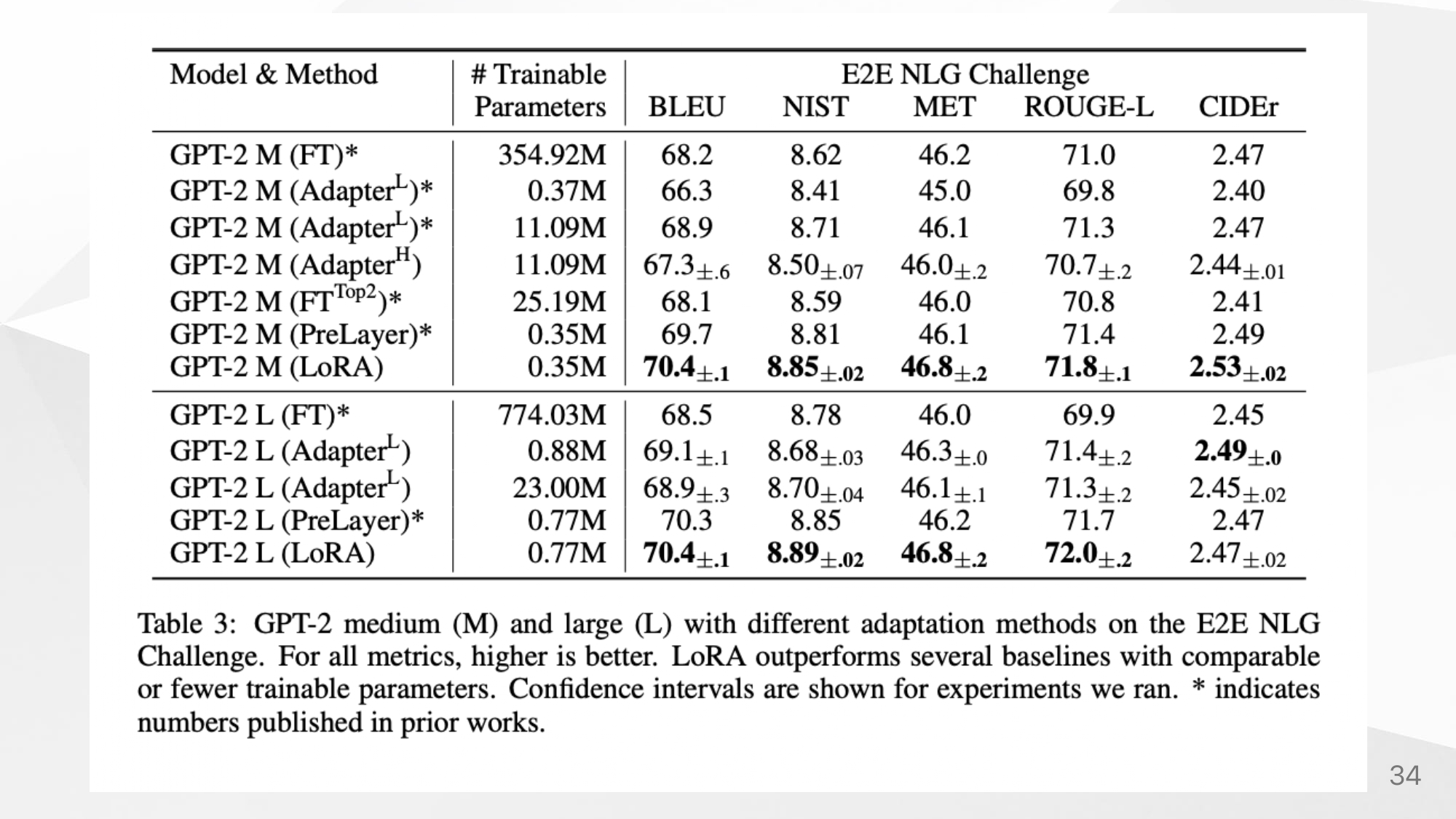
NLG
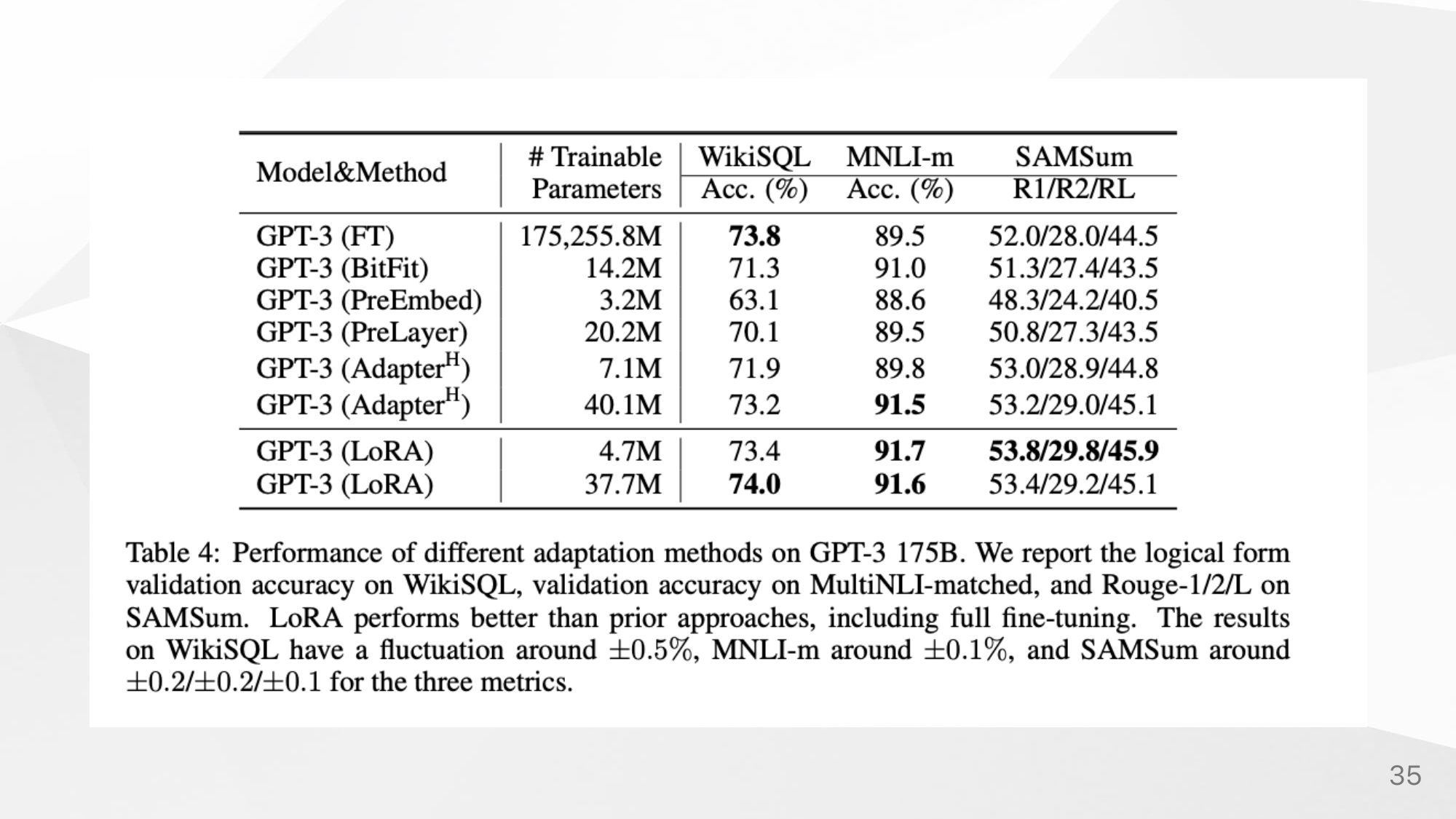
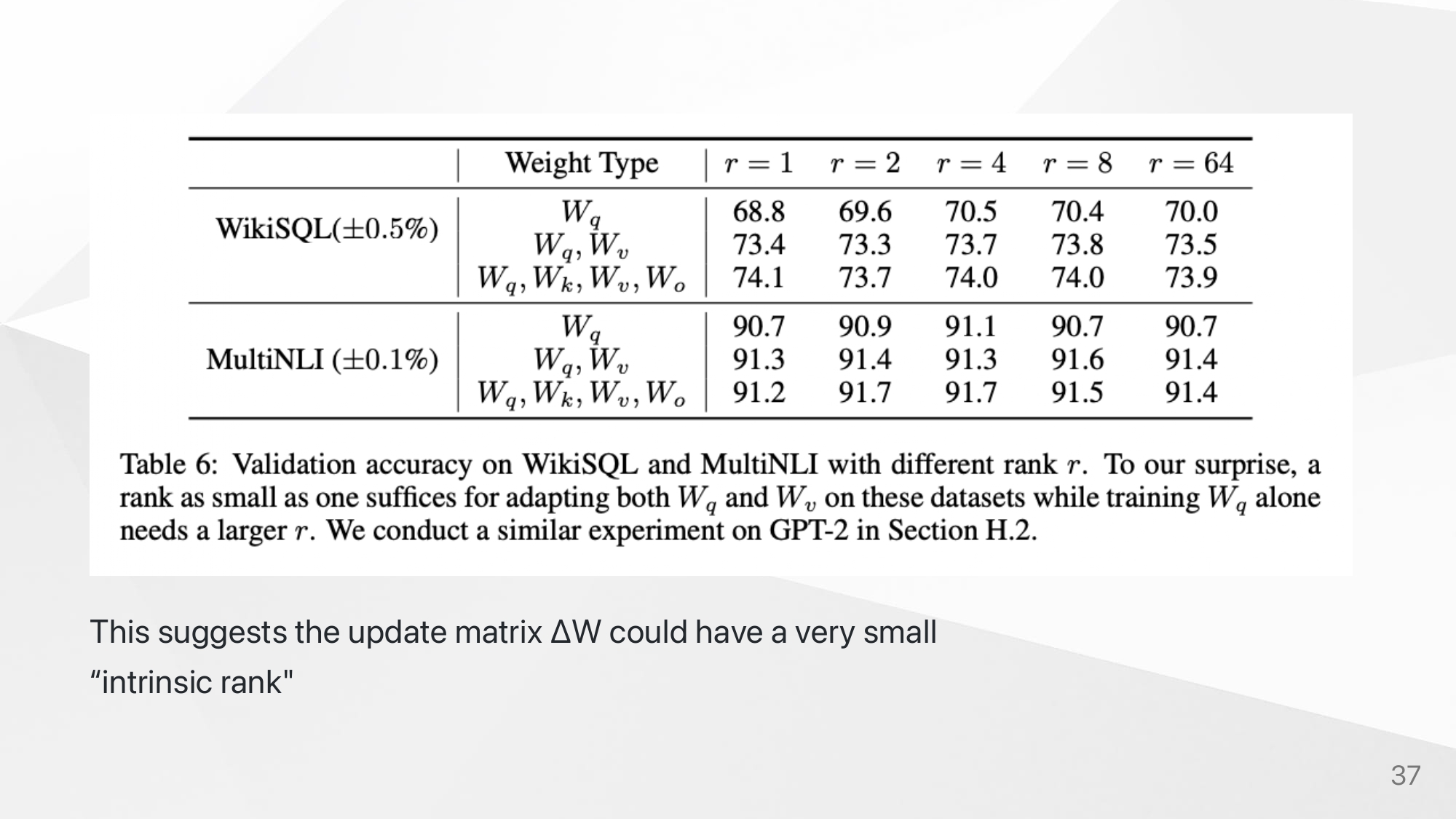
Proof of intrinsic rank
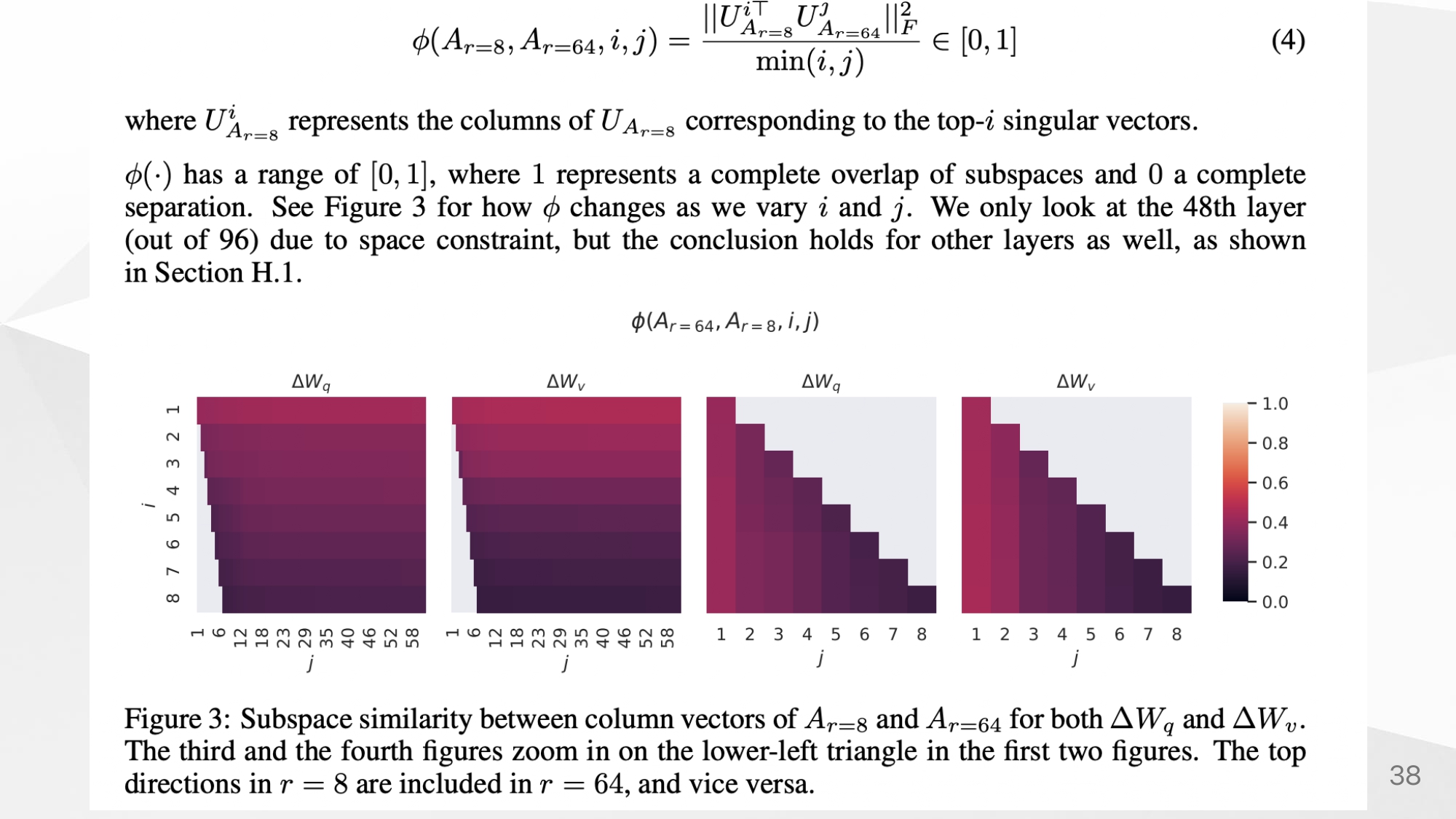
similarity about and
Conclusion


LoRA paper
https://arxiv.org/abs/2106.09685
alpha값과 initialize에 대한 글