SimCLR

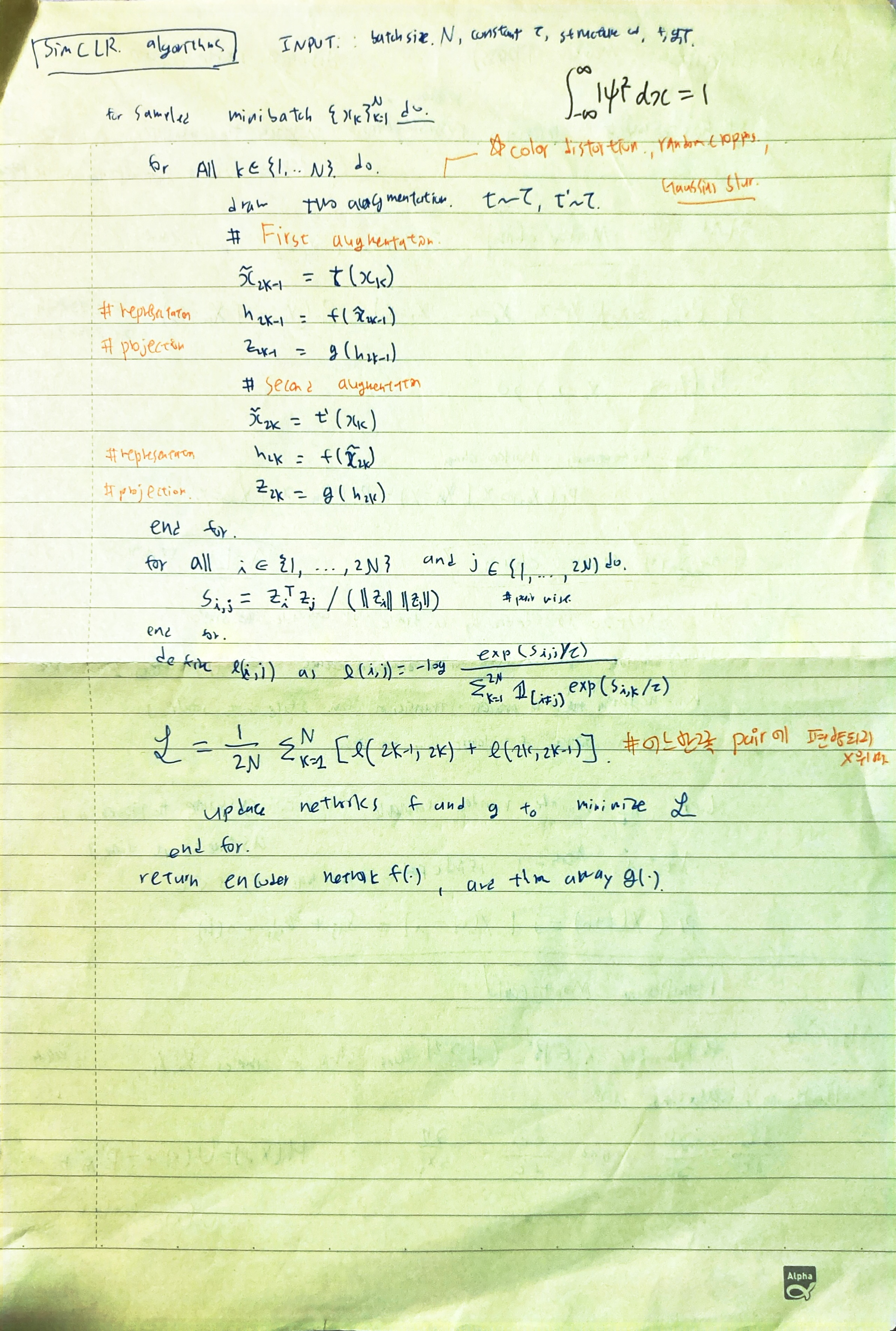
data augmentation를 이용해서 positive, negative data를 만들어주는것이핵심.
positive pair, negative pair에 대해서 softmax 처럼 취해줘서 , cross entropy 형식의 form을 lossfunction을 쓰는것이 핵심.

my project

아이디어 : 임베딩된 벡터들을 orthonormal한 basis로 변환한다면, 거리는 바뀌지 않는다. 이것을 이용해서 완성된 모델의 값들은 고정해둔채, 새로운 데이터에 대해서 aliment와 uniformity를 바꾸는것은 어떤지?

my project Objective function

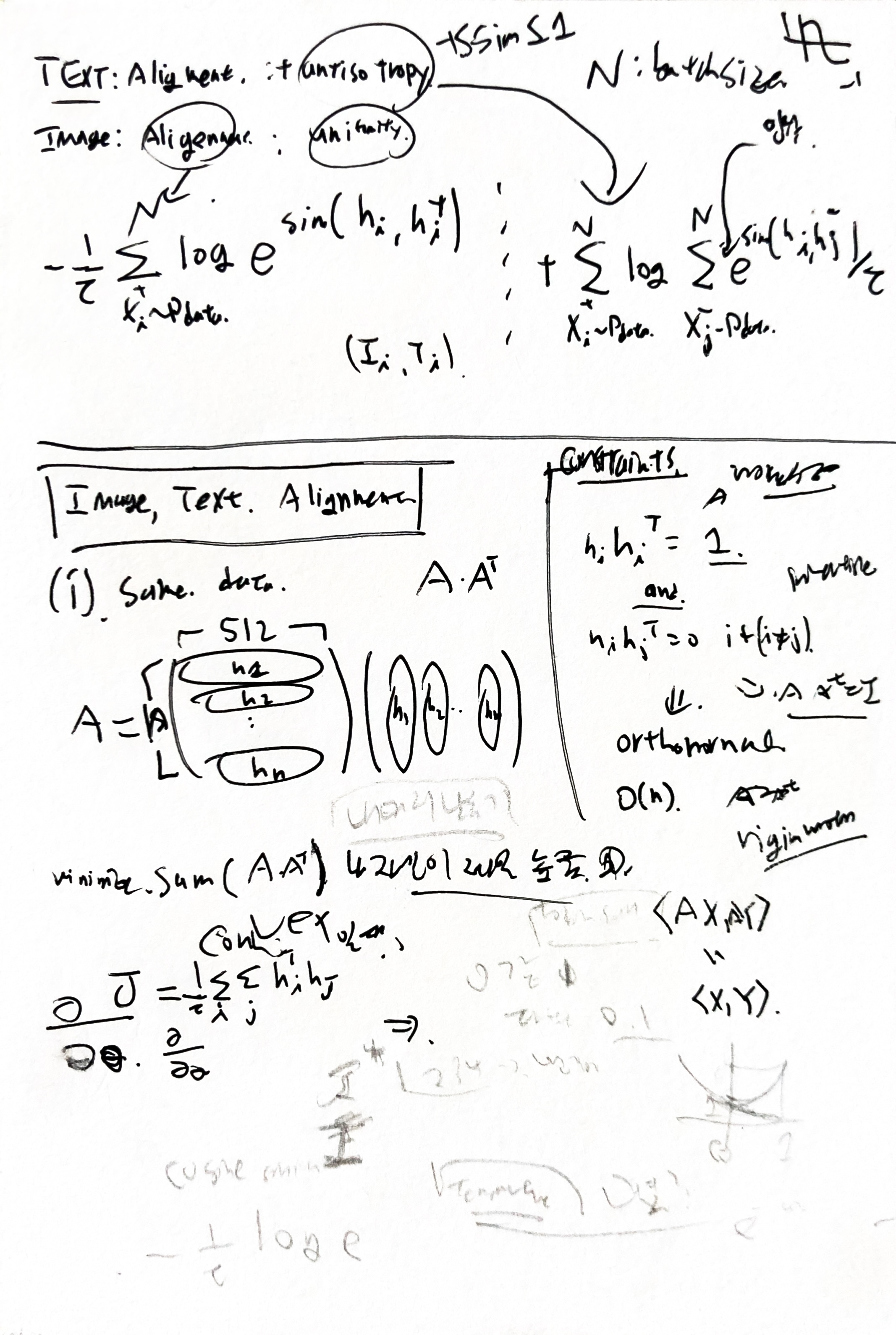
과연 이게 잘되는것인지. 계산해 볼수 있을까? 추측할수 있을까?

GAN with VAE sampling

GAN에 대해서 이해가 되지않는다면 코드를 참고삼아 보면 더욱더 잘이해가된다.
D(x) = 1 이면 진짜이고, D(x) = 0 이면 가짜로 판별한다. 그래서 loss term을 두개를 두는데 D(G(z))=1으로 하나는 만들어서 , binary cross entropy loss를 태우고, 다음번은, 아래 사진처럼 또하나의 BCE를 만들어서 태운다.

또 생각난것은 , z를 gaussian random 샘플링하는데,그 대신에 VAE를 통해 Z를 샘플링하고, VAE의 Deocder를 GAN모델의 generator의 inital weight과 모델로 쓰면 어떨까 생각을 해보았다. 뭔가 그럴듯 하지만, 실제 backpropa를 시키는 값들을 단순하게 계산만해보아도, discriminator함수의 partial gradient term이 추가되기때문에, 전혀 다른 Loss function을 형성하게된다. 그래서 결국, optimal한 generator weight은 VAE때와 전혀 다르게 작동한다. 실제로 실험 해보면, 초기에는 vae처럼 generator가 생성을하다가 nosiy하게 값이 바뀌고 다시 optimal한 값들을 찾아나간다.

markov chain

먼저 markoc chain - discrete state space
stochastic model describing sequence of possible states in which the probability each event depends only on the state

이산시간 마코브 체인

두 조건부확률이 잘 정의된경우. 양수이다. time-homogeneous markov chain,

A = LU 분해 가능

연속 시간 마코브 체인

헤밀토니안 몬테카를롤

Hamiltonian's equation