SCP
SCP(SC CP PN) 릴레이션
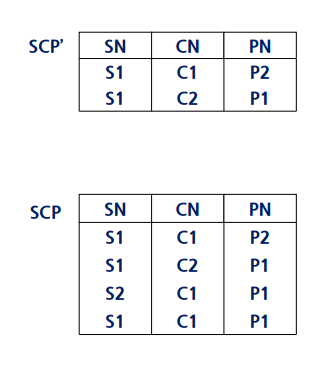
SCP 릴레이션은 4NF릴레이션이다. 이를 두개의 애트리뷰트로 분리해서 SN CN으로 나누면 SN CN | CN PN | PN SN 이다. 이는 R(A B C)를 분해하는것과 비슷하다.
이렇게 나눠진 릴레이션을 조인해보면, 위조튜플이 생긴다.

즉 이렇게 2개로만 분해하면 무손실분해가 성립하지 않는다. 따라서 1 2 를 먼저 조인하고, 세번째를 조인해서 위조튜플을 모두 지워내야한다.
5NF
N way cyclic constraint를 만족하면 n분해 릴레이션이라고 한다. (SCP는 3분해)
n-분해 릴레이션(n>2) -> n개의 프로젝션만으로 무손실 분해될 수 있으며, n보다 작은 프로젝션으로는 무손실 분해가 불가능함
조인종속
대부분 2 way 분해를 하지만 scp의 경우 3개로 분해해야함
이때 jd를 만족한다고 할 수 있다.
- 4개 같은 경우 현실적으로 사용하기가 어려워서 존재하지 않는다.
A,B,...,Z 를 각각 R의 애트리뷰트들에 대한 진 부분 집합이라 할 때 릴레이
션 R이 그의 프로젝션 A, B, ..., Z의 조인과 동일하면,
R은 JD *(A, B, ..., Z)를 만족한다.
또한, 릴레이션 R(A,B,C)가 JD *(AB,AC)를 만족하면,
한 쌍(2)의 MVD A ↠ B|C도 성립.
JD는 MVD의 일반형이다.
예시
SCP 릴레이션은
◦ JD *(SC, CP, PS)를 만족
◦ 3-분해 릴레이션
-> JD를 만족하는 n-분해 릴레이션은 n개의 프로젝션으로 분해해서 보관해야함.
이상
-
삽입이상
SCP’ 에 S2 C1 P1 을 삽입하고자 할 떄, S1 C1 P1도 추가를 해야 3개로 분해했을떄 원래것이 나오게 된다. -
S1 C1 P1을 삭제하려고 하면 다른 튜플중 다른 하나를 삭제해야함 즉, S2 C1 P1이 삭제되어야 함
이상의 원인 scp가 3분해 릴레이션
해결 : 릴레이션을 3개로 분해해서 유지해야 한다
5NF의 활용
제 5 정규형을 사용하는 경우는 매우 드물다
릴레이션 R 에 존재하는 모든 조인종속이 R의 후보키를 통해 성립하면 R은 5NF
프로젝션-조인 정규형(PJ/NF; projection-join normal form) 이라r고도 한다.
- 후보키를 조인 애트리뷰트 하는 조인종속
- 이 JD에 포함되는 애트리부트 부분집합은 모두 R의 슈퍼키가 된다
예시
예1:
◦ 릴레이션 SCP는 JD *(SC, CP, PS)를 만족하지만,
후보 키 (SN,CN,PN)을 통하지 않으므로 5NF이 아님
◦ 그러나 SC, CP, PS는 5NF – 어떤 조인 종속도 포함하고 있지 않음
학생(학번,이름,학과,학년) 릴레이션의 기본 키가 학번이고 후보 키가 이름일 경우
- JD *((학번,이름,학과), (학번,학년)) or
- JD *((학번,이름), (학번,학년), (이름,학과))
- 이 JD는 모두 후보 키를 통해 성립, 5NF
- 프로젝션 애트리뷰트들은 모두 슈퍼키 임
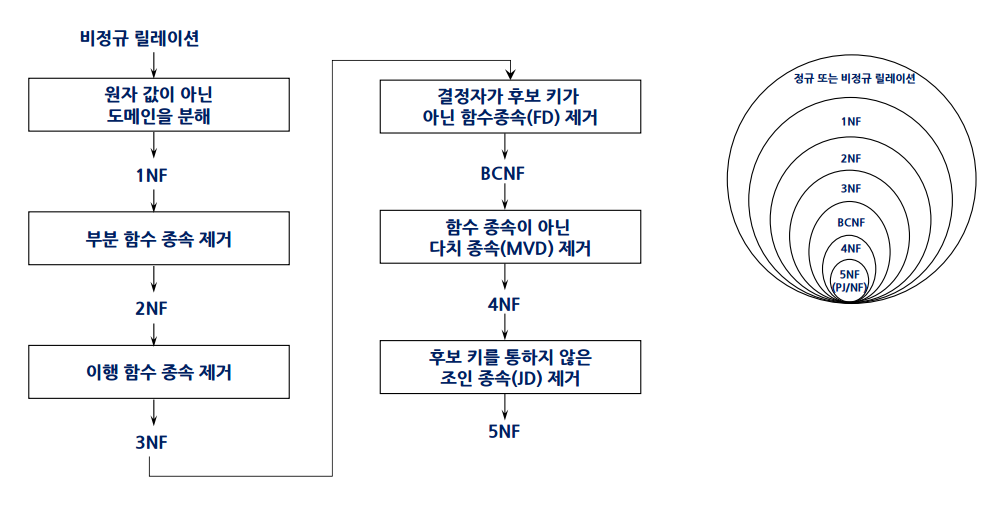
정규화과정과 포함관계
데이터모델링
데이터 설계
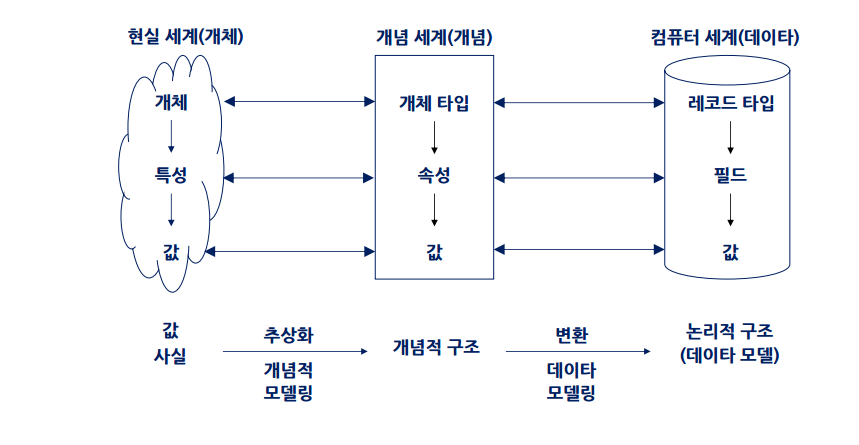
현실 : 개체 -> 특성 -> 값
- 추상화 (개념적 모델링)
개념 : 개체타입 -> 속성 -> 값
- 변환(데이터 모델링)
데이터 : 레코드타입 -> 필드 -> 값
데이터세계에 있는 모델을 현실세게의 모델로 하려면 ER 모델로 수렴한다. 개념을 ER모델화 하고 데이터 모델링을 통해 관계형데이터모델로 데이터화 하고 데이터를 물리적 구조로 변환한다.
데이터 모델의 구성
D = S O C
S : 구조
- 데이터의 정적 성질
- 개체 타입과 이들 간의 관계를 명세
O : 연산
- 데이터의 동적 성질
- 데이터의 조작 기법
C : 제약 조건
- 데이터의 논리적 제약
- 데이터 조작의 한계를 표현하는 규정
데이터 모델은 관계 데이터 모델이 널리 사옹된다
현재는 최종적으로 객체 지향형 모델개념이 포함된 객체-관계 데이터 모델이 사용
개체 entitiy 관계 relationship 으로 구성되어 있다
개체타입과 에트리뷰트
개체
- 단독으로 존재할 수 있으며 다른 것과 구별되는 객체
개체타입
이름과 애트리뷰트들로 정의됨
- 개체 집합(entity set)
- 한 개체 타입에 대한 개체 인스턴스들의 집합
애트리뷰트
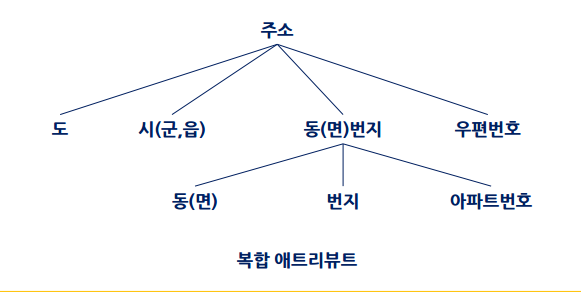
단순 애트리뷰트 : 더 이상 작은 구성원소로 분해가 불가능한 애트리뷰트
복합 애트리뷰트 : 여러 개로 분해할 수 있는 애트리뷰트
유도 : 다른 애트리뷰트나 개체가 가지고 있는 유도되어 결정되는 경우
저장 : 유도애트리뷰트를 생성하는데 사용한 것
널 애트리뷰트
널 값을 가지는 애트리뷰트
해당되지 않는다, 알 수 없다, 누락되었다
예
“성적” 애트리뷰트 : 저장 애트리뷰트
“평균 성적” 애트리뷰트 : 유도 애트리뷰트
"나이"애트리뷰트 : 저장 애트리뷰트
"생년월일" 애트리뷰트 : 유도 애트리뷰트
관계 타입
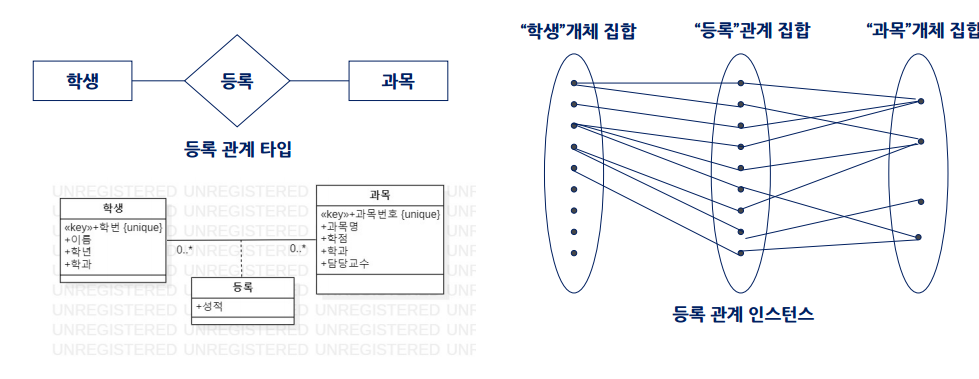
개체와 개체 사이에 relationship이 있음. 예를 들어,
학생 <-> 과목 두 집합이 있을 떄, 수강한다는 relationship이 있음. 이떄, 두 개체를 연결하는 선들의 집합 (인스턴스)
관계타입의 유형
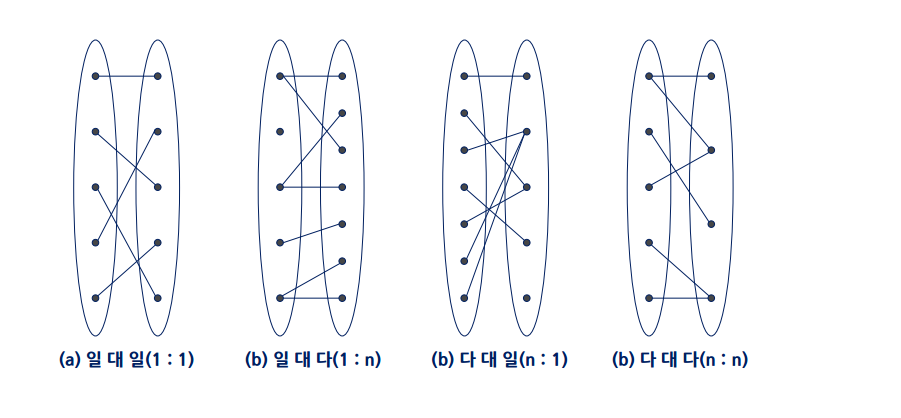
1 : 1 (one to one: 일 대 일)
1 : n (one to many: 일 대 다)
n : 1 (many to one: 다 대 일)
n : m (many to many: 다 대 다)
전체참여와 부분참여, 존재종속
전체 참여
모든 객체과 ab에 참여
교수 – 학과 관계
부분 참여
a b 관계에서 a의 일부 개체만 a b 관계에 참여
학생(휴학생 제외) 일부만 참여
존재종속
- 어떤 개체 b의 존재가 개체 a의 존재의 종속된다
- B는 A에 존재종속
- A 주 개체, B 종속 개체
예를 들자면 다음과 같은것이 있다.
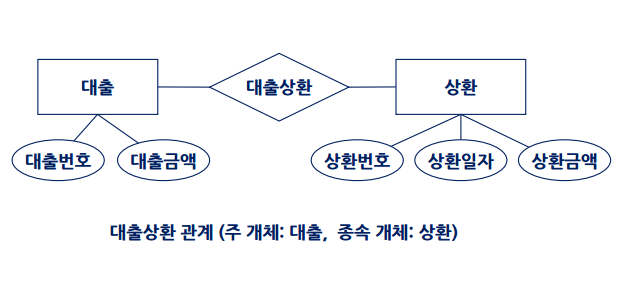
대출 – 대출 상환 – 상환
대출을 받지 않고 대출상환이 발생할 수는 없음
즉, 상환이라는것은 대출이 없으면 존재하지 않음
대출 – 주 개체, 상환 – 종속 개체
ER모델
정의
개체관계모델로, 1976년 피터 챈이 고안함. 개념적 데이터 모델이고 현실세계를 개념적으로 표현하기 위해 사용한다.
- 개체 타입(집합)과 관계 타입(집합)을 기본 개념으로 현실세계를 표현하는 방법
그래픽 표현

-
개체 집합
- 한 개체 타입에 속하는 모든 개체 인스턴스
-
관계 집합
- 한 관계 타입에 속하는 모든 관계 인스턴스
예시
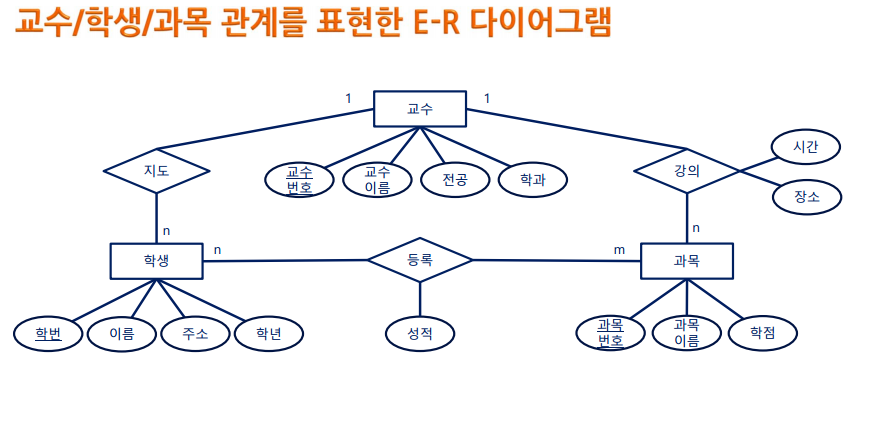
특징
- 다대다 관계이다.
- 다원 관계 이다 - 두개 이상의 개체타입의 하나의 관계에 관련 가능하다.
- 다중 관계 표현이다. - 두 개체 타입 사이에 둘 이상의 관계가 존재 가능하다.
- 관계타입도 애트리뷰트를 가질 수 있다.
키 애트리뷰트
한 개체 집합 내에서 각 개체마다 상이한 값을 갖는 애트리뷰트나 애트리뷰트 집합
- 키
- 개체 타입 내의 모든 개체 인스턴스들을 유일하게 식별한다
- 동일한 키 값을 갖는 두 개의 개체 인스턴스는 없다
- ER다이어그램에서 밑줄로 표시한다.
약한 개체 타입
-
튜플들을 유일하게 구분해주는 키 처럼 보이지만, 정확히 어떤건지 파악할 수 가 없음
-
어떤 의미인지 정확하지가 않음 따라서 다른 애트리뷰트가 하나 무조건 필요함
-
이러한 약한 개체를 설명해줄 수 있는 개체를 강한 개체라고 함
구별자
강한 개체와 약한 개체 집합 내에서 이들을 서로 구별 할 수 있는 애트리뷰트이고 이를 부분 키라고 한다
예시
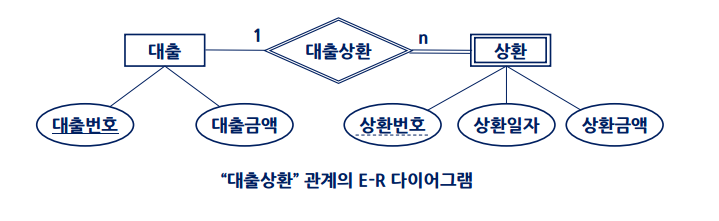
위와 같은 다이어그램에서 상환은 자기자신의 애트리뷰트들만으로는 상환번호라는 구별자를 명세할 수 없다. 따라서 상환은 약한 개체타입이다. 대출은 개체타입이고 강한 개체타입, 주 개체이다.
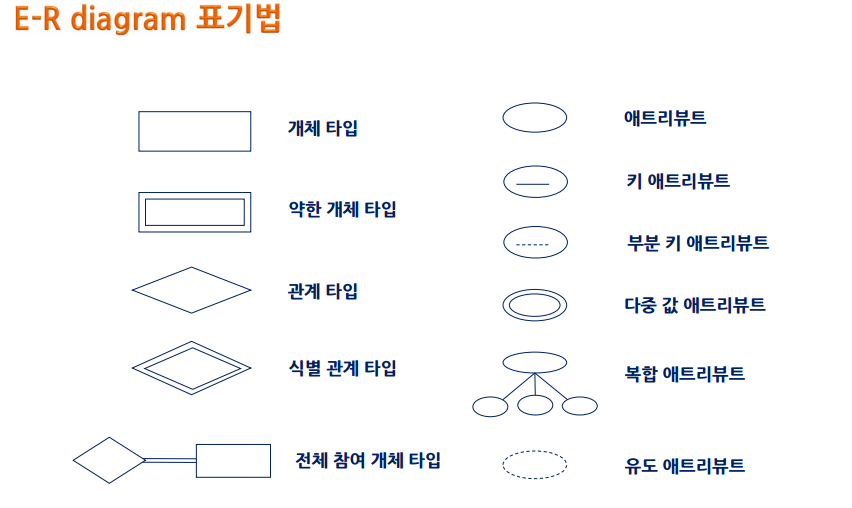
ER다이어그램 표기법
다른 데이터 모델
논리적 데이터 모델
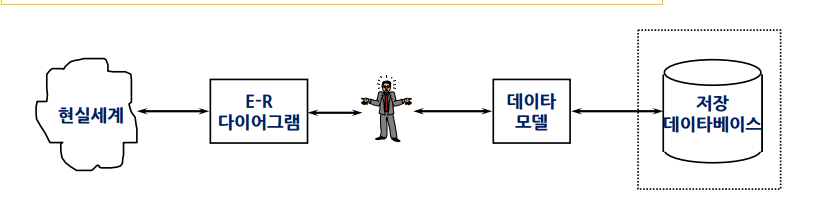
- 개념적 구조를 데이타베이스로 구현하기 위한 중간 단계로
논리적 개념인 레코드(개체) 타입과 관계로 표현
- 개념적 데이터 모델
- 개체-관계 데이터 모델
- 현실 세계를 추상적 개념인 개체 타입과 관계 타입으로 표현
네트워크 데이터 1950 1960
계층 데이터 모델 1950 1960
관계 데이터 모델 1990 ~ 현재
객체지향 데이터 모델 1980 ~ 이제 안씀
객체-관계 데이터모델 1990 ~ 현재
대부분 관계 데이터 모델로 함