Self Balance Tree

SBT

왜 이게 필요한가?

트리의 길이가 균형적이지 못하고 한쪽으로 치우쳐저 있다면, 검색을 할 때 평균적인 검색결과값을 보장하지 못한다. 이에 우리는 다양하게 스스로를 rebalance 할 수 있는 트리를 고안했는데 이번에는 그중 2가지 AVL과 Red Black을 알아보도록 하겠다. B-Tree의 경우 데이터베이스 글에서 그 흔적을 찾아볼 수 있다.

AVL

AVL 트리란 모든 노드에서 왼쪽 서브트리와 오른쪽 서브트리의 높이의 차가 1 이상이 아닌 트리를 말한다. 즉 한쪽으로 쏠려 있지 않은 트리를 말하는 것이다. AVL 트리에서의 탐색은 기존 이진탐색트리에서의 탐색과 동일하다. 특이한 점은 삽입과 삭제이고, 이 삽입 삭제 연산 과정에서 위에서 말한 높이 차를 맞추기 위한 회전이 실행된다.

회전

출처

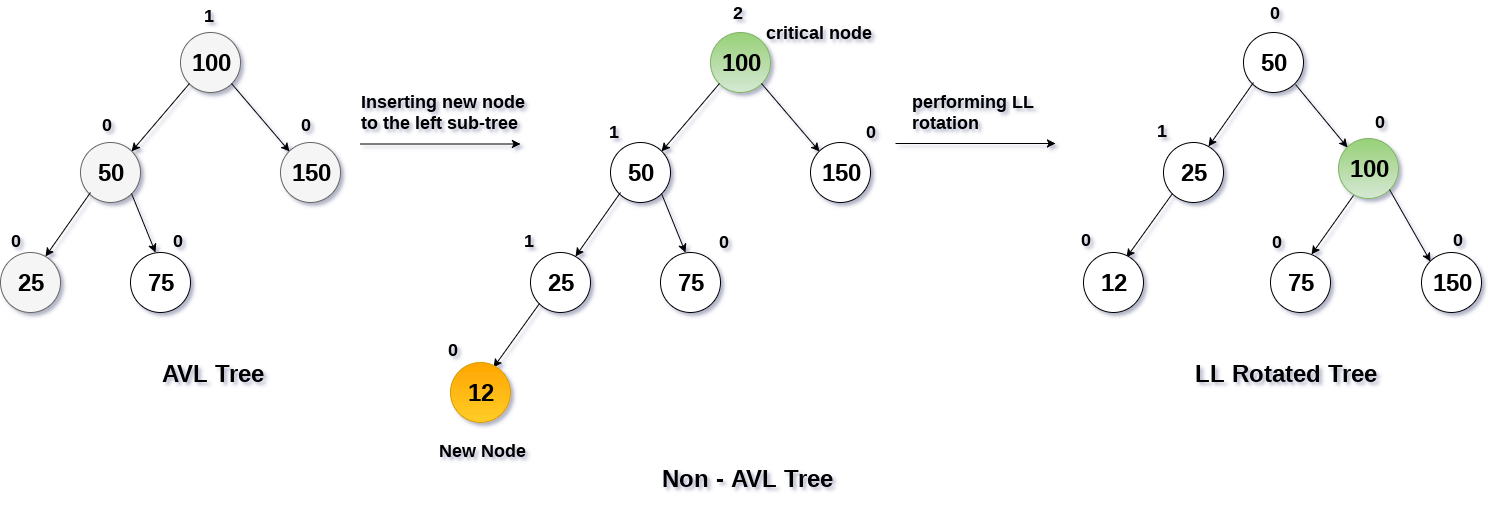
LL Rotate

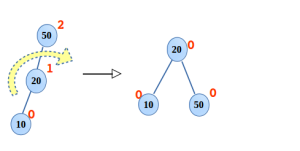
그림에서 보이는것처럼 해당 트리는 왼쪽으로 치우쳐진 트리이다. 이 트리를 균형잡으려면 LL Rotate를 통해 가운데 값을 parent로 만들고 가운데 값의 부모를 우측 자식으로, 으측자식은 자신의 부모의 좌측 자식으로, 그리고 자신의 좌측은 자기가 그대로 가지는 형태를 취하면 균형잡힌 트리로 변한다.

    def rotateLL(self, A):
        B = A.left
        A.left = B.right
        B.right = A
        return B

A노드(50)을 기준으로 회전한다고 하면 B = 20이 된다. A의 좌측자식을 b의 우측자식으로 다시 설정하고 (None) b의 우측자식에 a를 연결한다.

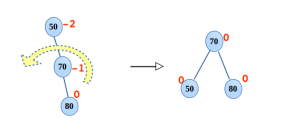
RR Rotate

위 과정의 정확히 반대이다.

    def rotateRR(self, A):
        B = A.right
        A.right = B.left
        B.left = A
        return B

가끔 교재에 따라 이를 반대로 표기하기도 한다.

하지만 이렇게 회전을 함에도 불구하고 추가회전이 필요한 그래프들이 존재한다. 이떄는 LR, 혹은 RL회전을 사용한다.

RL & LR Rotate

이 회전은 루트노드 A의 오른쪽 자식 B의 왼쪽 서브트리 추가시 발생하는 회전이다. 우선 B를 기준으로 LL회전을 하고 그 결과값을 A의 오른쪽 자식으로 삼는다. 그리고 다시 한번 A를 기준으로 RR회전을 시행하면 C가 부모노드가 되고, A, B는 각각 좌측 우측 자식이며, C의 좌측 자식은 A의 우측자식이 된다.

반대로 LR 회전은 A 루트노드의 왼쪽자식의 오른쪽 서브트리의 추가가 발생하면 생기는 회전이다. B를 기준으로 RR회전하여 C를 부모로 B를 C의 좌측 자식으로 만들고 C의 좌측자식을 B의 우측자식에 넣는다. 그 후 C를 다시한번 LL 회전하면 C가 부모, B A가 왼쪽 오른쪽 자식, 그리고 최종적으로 C의 우측자식은 A의 좌측자식이 되면서 마무리된다.

    def rotateRL(self, A):
        B = A.right
        A.right = self.rotateLL(B)
        return self.rotateRR(A)

    def rotateLR(self, A):
        B = A.left
        A.left = self.rotateRR(B)
        return self.rotateLL(A)

알고리즘들이 대부분 그렇지만, 구현은 쉽지만 이해가 어려운 그런 알고리즘이다.

AVL 재균형

이렇게 회전함수들을 공부했으니, 이제 언제 이 회전함수를 쓰는지 알아야한다. 그럴려면 우선 좌측 우측의 높이차를 구하는 함수가 필요하다.

  def calc_height_diff(self, n):
        left = self.calc_height(n.left)
        right = self.calc_height(n.right)
        return left - right

height diff는 좌측 우측 높이의 차를 구해주는 함수이다.
이 값을 통해 우리는 어느쪽이 더 높은지, 얼마만큼 벗어나 있는지 파악할 수 있다.

1. 만약 차가 1보다 클 경우 --> 왼쪽이 더 길다는 뜻
   1.1) 부모 기준 좌측 서브트리의 높이를 비교한 후 그 값이 0보다 크다면 --> 좌측에 쏠려있다는 뜻이고 따라서 LL 회전을 한다.
   1.2) 만약 0이거나 그보다 크다면 우측 서브트리에 들어있다는 뜻이된다. 따라서 LR 회전을 한다.

2. 만약 차가 -1 보다 작은 경우 --> 오른쪽이 더 길다는 뜻
   2.1) 부모 기준 우측 서브트리의 값을 비교한 후 그 값이 0 보다 작다면 --> 우측 서브트리에 쏠려있다는 뜻이고 따라서 RR 회전을 한다.
   2.2) 만약 그렇지 않다면 좌측 서브트리에 값이 들어갔다는 의미이다. 따라서 RL 회전을 한다.

전체 코드

class node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

class AVL:
    def calc_height(self, n):
        if n is None:
            return 0
        hleft = self.calc_height(n.left)
        hright = self.calc_height(n.right)
        if hleft > hright:
            return hleft + 1
        else:
            return hright + 1

    def calc_height_diff(self, n):
        left = self.calc_height(n.left)
        right = self.calc_height(n.right)
        return left - right

    def rotateLL(self, A):
        B = A.left
        A.left = B.right
        B.right = A
        return B

    def rotateRR(self, A):
        B = A.right
        A.right = B.left
        B.left = A
        return B

    def rotateRL(self, A):
        B = A.right
        A.right = self.rotateLL(B)
        return self.rotateRR(A)

    def rotateLR(self, A):
        B = A.left
        A.left = self.rotateRR(B)
        return self.rotateLL(A)

    def reBalance(self, parent):
        diff = self.calc_height_diff(parent)

        if diff > 1:
            if self.calc_height_diff(parent.left) > 0:
                parent = self.rotateLL(parent)
            else:
                parent = self.rotateLR(parent)
        elif diff < -1:
            if self.calc_height_diff(parent.right) < 0:
                parent = self.rotateRR(parent)
            else:
                parent = self.rotateRL(parent)
        return parent

    def insert_avl(self, parent, node):
        if node.key < parent.key:
            if parent.left is not None:
                parent.left = self.insert_avl(parent.left, node)
            else:
                parent.left = node
            return self.reBalance(parent)
        elif node.key > parent.key:
            if parent.right is not None:
                parent.right = self.insert_avl(parent.right, node)
            else:
                parent.right = node
            return self.reBalance(parent)
        else:
            print("Same key Error")

    def inorder(self, node):
        if node is not None:
            self.inorder(node.left)
            print(node.key, end=' ')
            self.inorder(node.right)

def main():
    avl = AVL()
    data = [7, 8, 9, 2, 1, 5, 3, 6, 4]
    for key in data:
        n = node(key)
        avl.insert_avl(n)

AVL을 이용한 맵

AVL 맵은 BST맵을 그대로 받아와서 사용한다.

Red Black 트리

레드블랙 트리 역시 SBT이다. 다만 좀 다른 방법을 사용하고, AVL보다는 느슨한 균형을 유지한다. 둘의 탐색 시간복잡도는 똑같지만, 레드블랙 트리가 삽입 삭제에 있어 더 빠르고 이에 더 많이 사용된다.

특성

① Root Property : 루트는 black 이다
② External Property : 모든 리프(NIL)는 black 이다
③ Internal Property : 노드가 red 이면 그 노드의 자식들(2개 노드)은 반드시 black 이다.
→ No Double Red(빨간색 노드가 연속으로 나올 수 없다.)
④ Depth Property : 루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 black 노드의 수는 모두 같다
→ 이를 black-height 라고 한다

이를 고려하여 트리를 구성하면 다음과 같다.

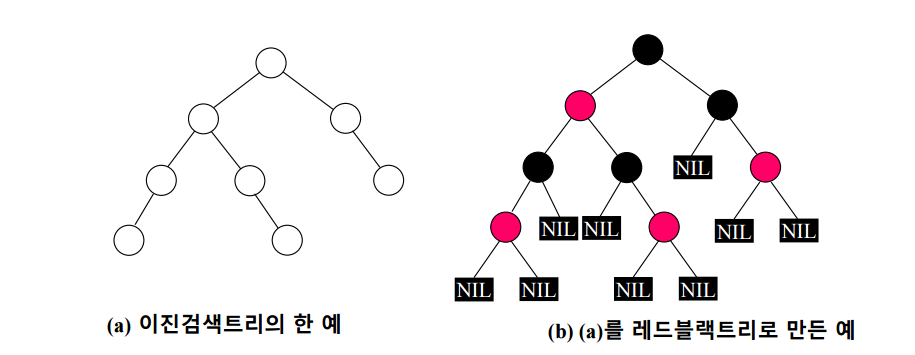
물론 실제로는 저렇게 많은 NIL을 쓰지 않고

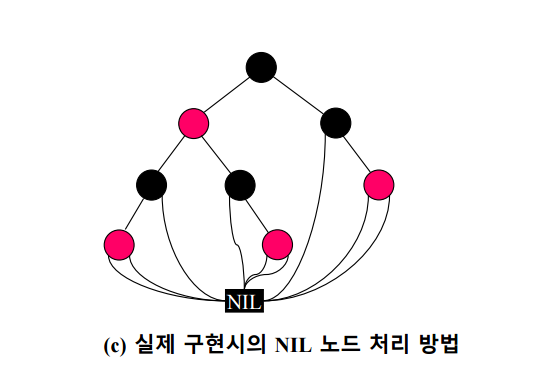
이런식으로 묶어서 처리한다.

레드블랙 트리의 회전

x를 중심으로 왼쪽 회전

y가 x의 부모가 된다.
y의 왼쪽 자식은 x의 오른쪽 자식이 된다.

y를 중심으로 오른쪽 회전

x가 y의 부모가 된다.
x의 오른쪽 자식은 y의 왼쪽 자식이 된다.

레드 블랙 트리에서의 삽입

1. BST에서의 삽입 알고리즘을 이용, 새 노드를 삽입한다.
2. 새롭게 삽입된 노드는 무조건 RED이다.
3. 이 후, 조건을 유지하기 위해 3가지 경우에 맞추서 처리한다.

새 노드는 항상 맨 아래쪽에 매달리므로 삽입 직후에,
x의 아래쪽은 블랙 노드인 리프 두개만이 있으므로 레드블랙특성을 위반하지 않는다.
• 그러므로, x의 위쪽에 문제가 발생하는지 확인하여야 한다.
• p(x의 부모)가 블랙이면 완료

만약 P가 red이면, 레드가 연속으로 나와서 특성이 깨진다. 따라서 P^2 (부모의 부모)sms 반드시 블랙이여야 한다. --> 새 노드 삽입 이전에 트리는 이미 레드블랙이기 떄문이다.
--> 이에 삽입된 x노드의 형제 노드 역시 블랙이여야 한다. 이때, x의 주변에 레드나 블랙이 둘다 가능한노드들을 s (삼촌) 이라고 부르자. P의 형제노드이다.

이떄 케이스를 3개로 나눈다.
Case 1: s가 red
Case 2: s가 black

• Case 2-1: x가 p의 오른쪽 자식
• Case 2-2: x가 p의 왼쪽 자식

케이스 1

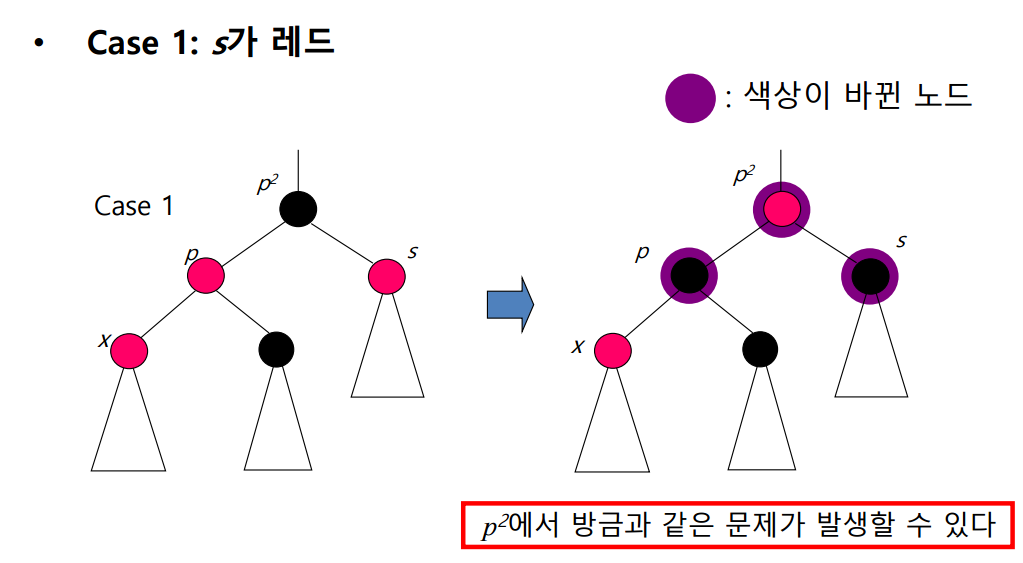
s가 레드일경우, p와 s의 색상은 레드에서 블랙으로 변한다.
그리고 p^2역시 이에 맞춰 레드로 바꾸게 된다.
하지만 이렇게하면 p^2 역시 충돌이 발생할 수 있다. 따라서
1. p^2가 루트이면 색을 블랙으로 다시 바꾸고 마무리한다.
2. p^2에게 조상이 있으면, p^2의 부모색을 확인한다. 그 결과:

✓ p2 의 부모색상이 블랙이면, 레드 블랙 특성 만족
– p2 : 레드, p2 부모: 블랙

✓ p
2 의 부모 색상이 레드이면, 레드블랙 특성 ③ 위반,
처음에 x를 삽입한 경우에 발생한 문제가 p2에 발생한다
– 재귀적으로 다시 시작한다.

케이스 2-1

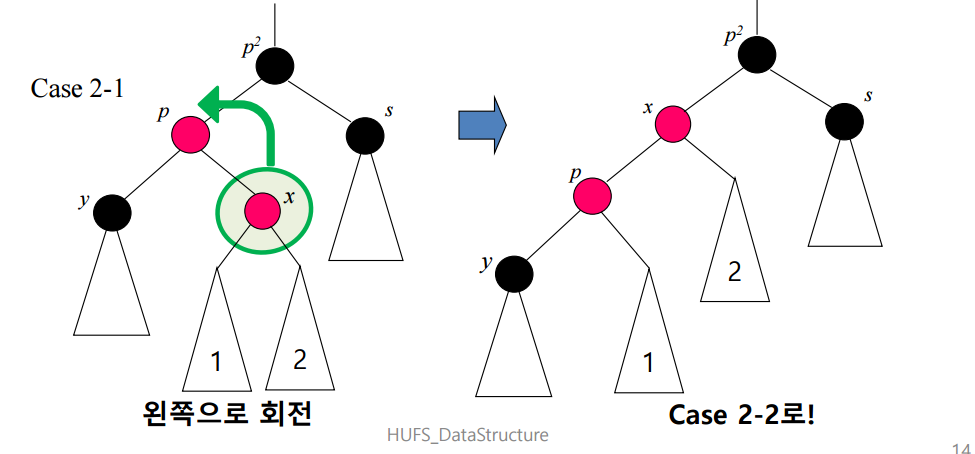
s가 블랙이고, x가 p의 오른쪽 자식을 경우 케이스 2-1이다. x를 RR회전한다. 그러면 그림과 같은 트리가 나오게 된다. 이는 아직 트리의 규칙을 위반하고 있는 케이스이다. 따라서 케이스 2-2로 진행한다.

케이스 2-2

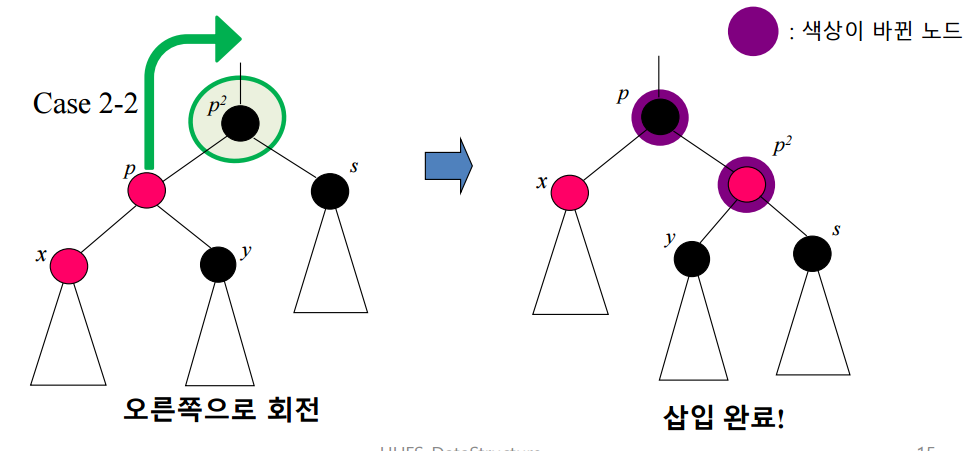
s가 블랙이고, x가p의 왼쪽자식일때 p^2를 중심으로 LL회전을 한다. 그 후 두 노드의 색상을 바꾸면 된다.

삭제

임의의 노드 X를 삭제한다고 했을 때, X의 자식이 둘이라고 한다면,
노드 x의 직후원소(오른쪽 서브트리에서 최소원소)인 노드 m을 노드 x에 복사한 후 노드 m을 삭제한다.

✓노드 x의 색상을 변경하지 않고 키값만 바뀌므로,
레드블랙 특성을 위반하지 않는다.

✓문제발생은
노드 x의 직후원소 노드m을 삭제한 후, m 주변이 레드블랙 트리 특성을 위반했을 때이다 하지만, 최소원소 노드 m은 왼쪽 자식을 갖지 않는다.

즉, 최소원소 노드 m은 최대 하나의 자식만 가질 수 있다.

따라서 자식이 없거나, 자식이 하나인 노드의 삭제 작업과 동일하다 할 수 있다.

예시

삭제하려는 노드 x(최대 한 개의 자식을 갖는다)의 자식을 m
이라 가정하자
• x의 자식이 없으면, m은 NIL 노드이다.
• 삭제되는 노드 x는 자기 부모의 왼쪽 또는 오른쪽 자식일 수도 있다. 둘 중 하나만 설명해도 완결성이 떨어지지 않음
• x는 자기 부모의 왼쪽 자식이라고 가정하자

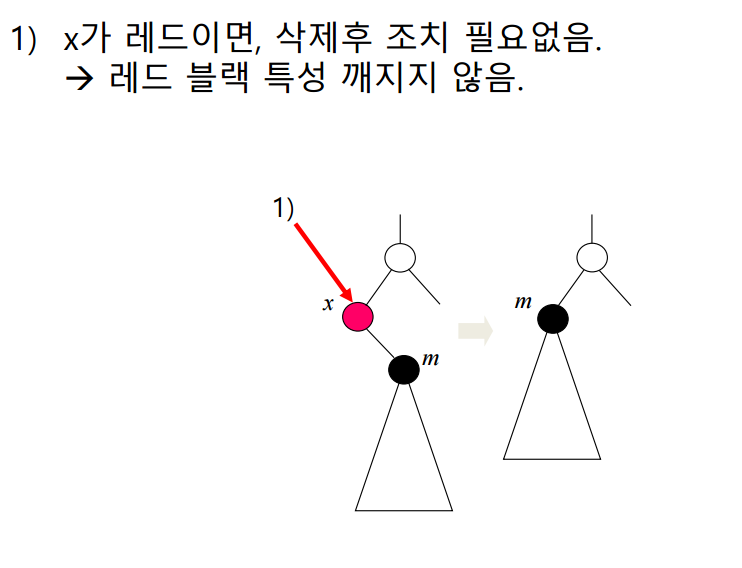
x가 레드일면 삭제 후 조치가 필요 없다. 자식은 무조건 블랙이고 그냥 위치가 바뀐것이기 때문이다.

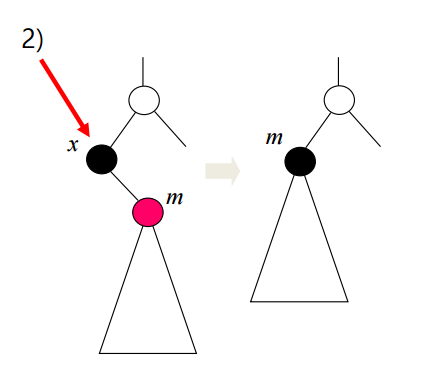
마찬가지로 X가 블랙이고 m이 레드이면 삭제 후 색상을 바꾸면 조건을 다시 만족한다.

하지만 둘다 블랙인 경우, 루트간의 블랙노드 개수가 맞지 않는 오류가 발생하고 이를 7가지 케이스로 나눠서 살펴봐야한다.

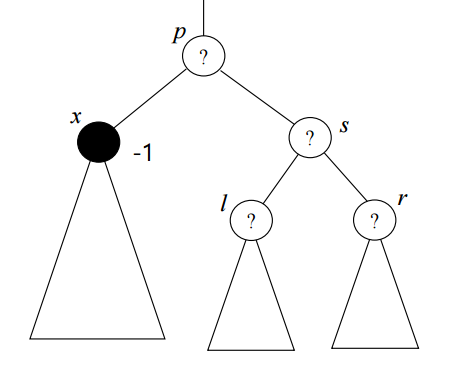
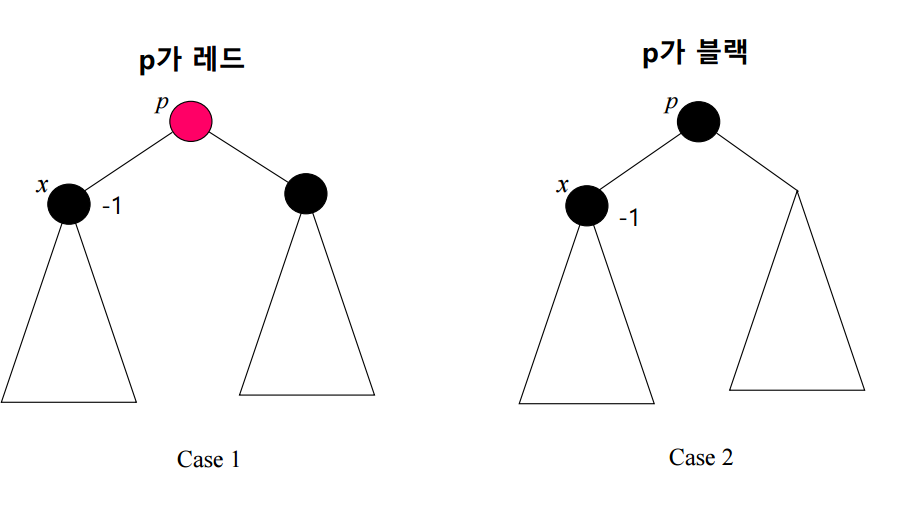
전체 케이스를 살펴보면 다음과 같다

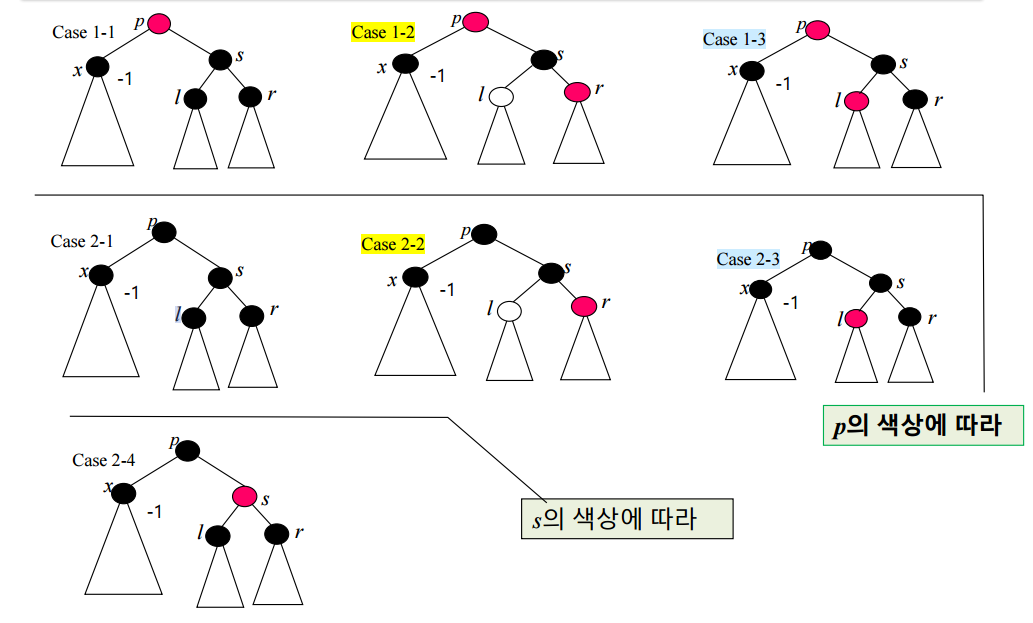
하지만 줄이고 줄이다보면 다음과 같은 형태가 된다

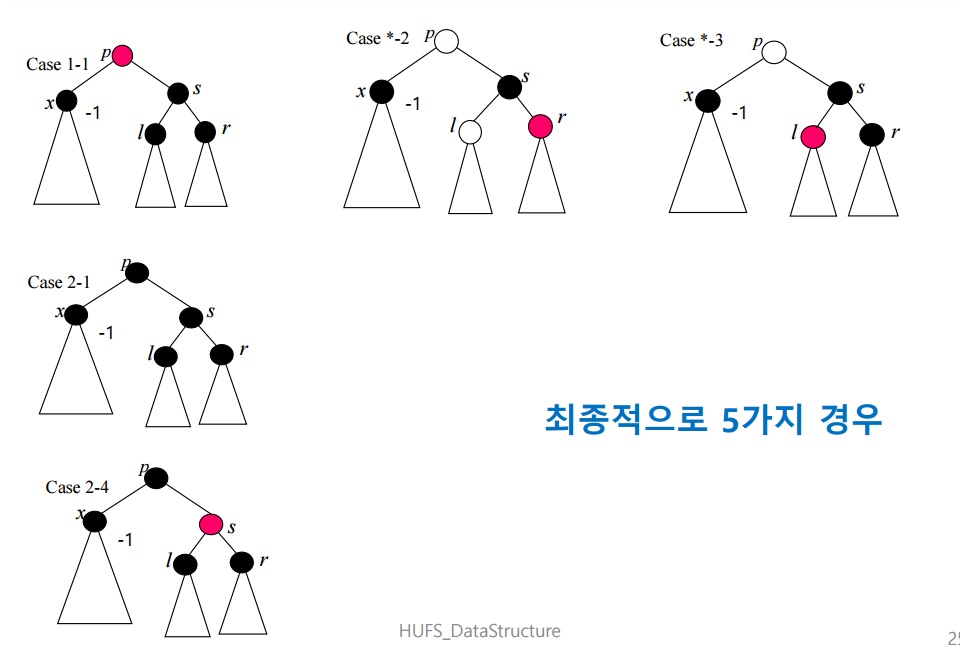
Case 1

p가 레드(s는 항상 블랙이므로) <l, r의 색상>에 따라
➢ Case 1-1 <블랙, 블랙>
➢ Case 1-2 <*, 레드> → <black, red>, <red, red>
➢ Case 1-3 <레드, 블랙>

Case 2 : p가 블랙 <s, l, r의 색상>에 따라

➢ Case 2-1 <블랙, 블랙, 블랙>
➢ Case 2-2 <블랙, *, 레드>
➢ Case 2-3 <블렉, 레드, 블랙>
➢ Case 2-4 <레드, 블랙, 블랙>

색상별 접근

Case 1-1 <블랙, 블랙>

l, r 색상이 블랙 블랙인 경우, p와 s의 색상을 바꾼다. 그러면 x로 가는 경로에 블랙이 하나 모자라던것ㅇ ㅣ해결된다.

r이 레드가 l이 자유선택인 경우

Case 1-2 <, 레드> → <black, red>, <red, red>
Case 2-2 <블랙, , 레드> <s, l, r의 색상>
s를 p RR회전한다. 그후 p와 s의 생상을 바꾼다. 그리고 r의 색상을 블랙으로 바꾼다. 이러면 각 경로의 블랙의 수가 똑같아진다.

l r이 <*, 레드, 블랙>인 경우

Case 1-3 <레드, 블랙>
Case 2-3 <블렉, 레드, 블랙>

l을 LL 회전 한다. 그 후 l과 s의 색상을 바꾼다. 그러면 r이 레드고 l이 자유선택인 케이스 2번과 동일해진다.

Case 2-1 <블랙, 블랙, 블랙>

1) s의 색상을 블랙에서 레드로 바꾼다.
2) s를 지나가는 경로에서도 블랙 노드가 한 개 부족하다. p 를 지나는 경로 전체에서 블랙 노드가 한 개 부족한 것이다.
✓이것은 x에 발생했던 문제가 p에도 발생한 것이다.
3) p를 문제 발생노드로 하여 재귀처리한다.

Case 2-4 <레드, 블랙, 블랙>

s를 RR회전한다. 그 후 p와 s의 색상을 뒤바꾸면 p는 레드, s는 블랙이다. 그 후 위의 케이스중 맞는걸로 바꾸면 된다.

시간복잡도

• 트리의 높이: O(log n)
• 검색: O(log n)
• 삽입
➢ case 1: case 1 재귀호출. O(log n)
➢ case 2: 상수시간.
• 삭제
➢ case 1-1, -2, -3: 상수시간
➢ case 2-4: case 1-1, 1-2, 1-3으로 이동. 상수시간
➢ case 2-1: 재귀호출이 필요할 수 있음. O(log n)
• ∴O(log n)

즉, 삽입과 삭제에서 경우에 따라 AVL이나 BST보다 빠른것을 알 수 있다.