Python Data Structures
1.리스트, 집합

리스트와 집합은 모든 자료구조와 알고리즘의 기초가 되는 자료구조이다. 따라서 이에 대해 학습해보도록 하겠다리스트, 혹은 선형 리스트는 항목들이 차례대로 나열되어 있는 선형 자료구조이다. 리스트들의 항목들은 순서 또는 position을 가진다. 집합과 다른점은, 리스트는
2.스택

출처(https://www.burgerking.co.kr/!\[](https://images.velog.io/images/blacklandbird/post/b9cd0819-b4d1-4e3b-94bb-a419f47f4299/93116ef9-43a4-45
3.Queue, Dequeue

큐라는건 대기열이다. 게임을 좀 해보신 분들이라면, 게임을 매칭할때 큐를 돌린다고 표현하는걸 알고있으실거다. 이는 게임매칭의 순서가 먼저 누른사람들끼리 잡아주기 때문이다. (물론 실제로는 그렇지 않다) 큐는 대기열이라 생각하면 조금 쉽게 이해가 될 것이다. 대기열의 가
4.정렬과 탐색 (1부)

정렬 특징 정렬이란, 어떠한 자료를 정해진 순서대로 정리하는것을 말한다. 정렬을 왜 하는가에 대한 대답은 우리 모두가 잘 알고있다. 정렬이 잘 되어있으면, 즉 정돈이 잘 되어있는 자료에서는 데이터를 찾아내기가 쉽기 때문이다. (나는 어지러진곳에서 더 잘 찾는다는 분들은
5.정렬과 탐색 (2부)
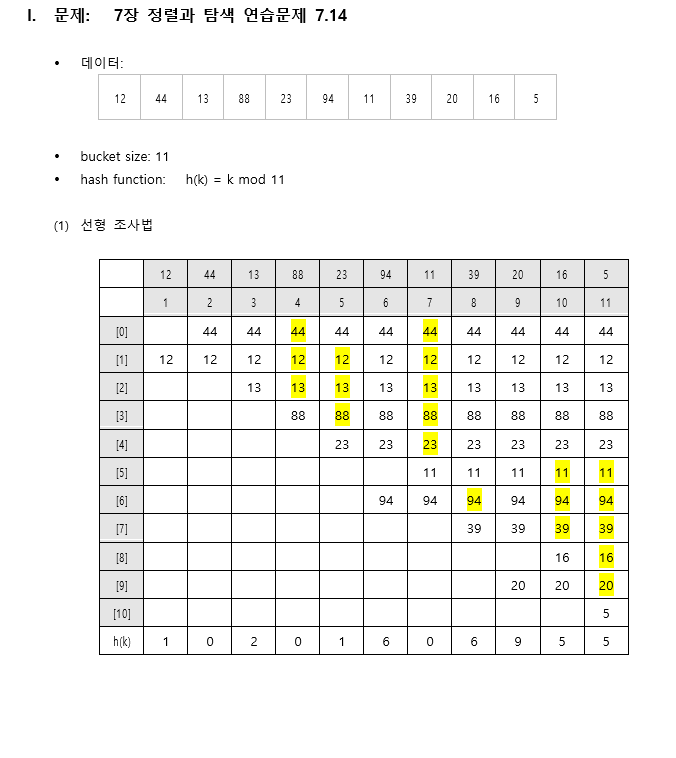
정렬을 하는 목적은 원하는 값을 더 빨리 찾기 위함이다. 즉, 정렬을 했으면 탐색을 해야한다는 의미이다. 순차탐색은 정렬되지 않은 테이블에서도 사용할 수 있는 가장 직관적인 탐색방법중 하나이다. 리스트롤 for문을 통해 1회 반복하면서 맞는 key가 있다면 반환하는 형
6.트리
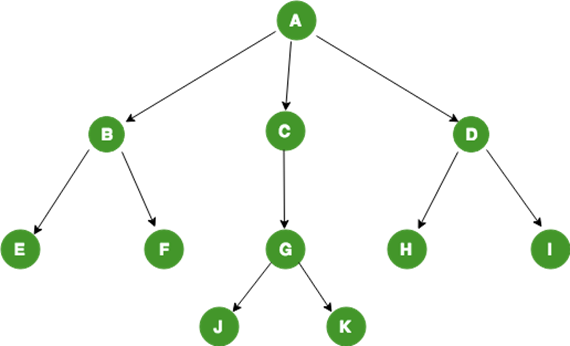
크리스마스 트리트리는 계층적인 구조를 나타내는 자료구조이다. 뒤집어진 나무를 생각하면 된다. 트리는 다음과 같이 생겼는데 각 하나의 원을 노드라고 부른다. 노드는 linkedlist에서도 사용해봐서 알 것이라 생각한다. 사실 트리는 또다른 형태의 linkedlist라고
7.힙

힙의 사전적 의미는 더미라고 한다. 힙은 완전이진트리 기반의 자료구조이다. 최대값, 혹은 최소값을 root에 올리고 이를 바탕으로 빠르게 값을 찾는 트리이다. 힙의 특징이라면 느슨한 정렬을 유지한다는 점이 있다. 힙은 루트가 최대값인 Max, 최소값인 Min 두가지 종
8.이중탐색트리

지금까지 우리는 신명나게 트리를 만들고, 이진탐색 트리를 만들고, 결정트리를 만들었다. 이젠, 트리로 탐색을 할 차례이다. 이진탐색트리의 각 노드에는 키값, 그리고 value가 들어간다. 일단 value는 당장 사용하지 않을것이기에 None, 혹은 ABCD 순으로 저장
9.Self Balance Tree
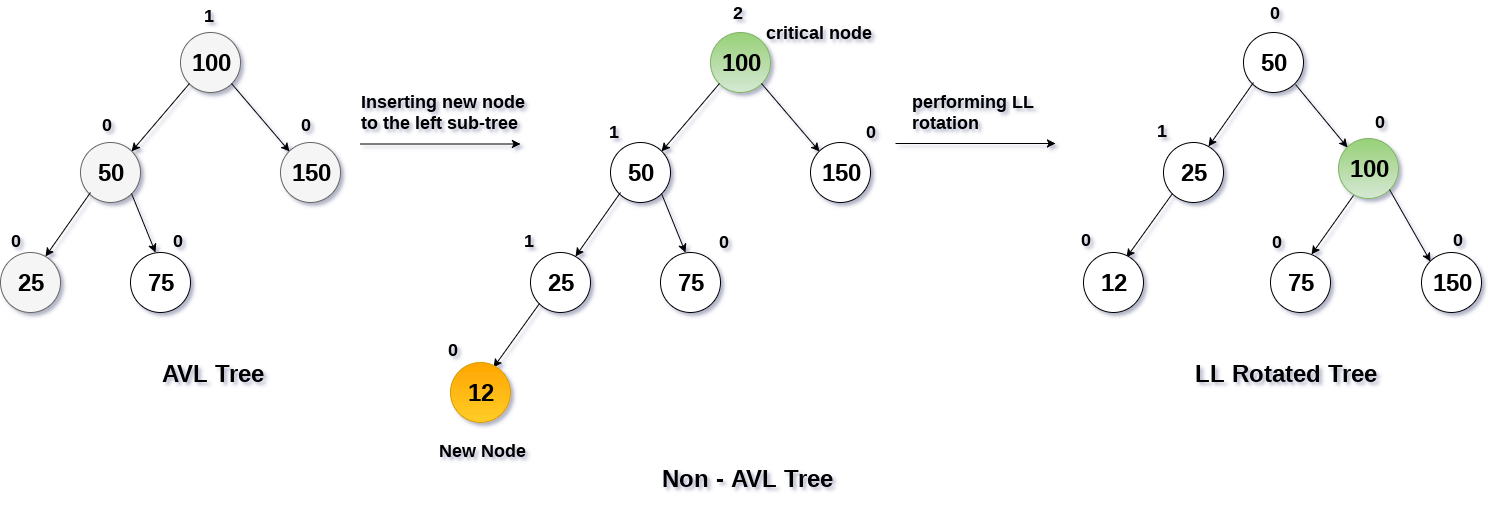
트리의 길이가 균형적이지 못하고 한쪽으로 치우쳐저 있다면, 검색을 할 때 평균적인 검색결과값을 보장하지 못한다. 이에 우리는 다양하게 스스로를 rebalance 할 수 있는 트리를 고안했는데 이번에는 그중 2가지 AVL과 Red Black을 알아보도록 하겠다. B-Tr
10.그래프

그래프는 과연 자료구조의 꽃이자 핵이라 할 수 있다. DFS, BFS, TREE, 다익스트라, 크루스칼, TSP, 해밀턴 이런 모든 알고리즘들이 전부 그래프에서 나온것이기 때문이다.그러면 그래프를 시작해보겠다.무방향 그래프 (Undirected Graph) 방향성이 없