탐색
정렬을 하는 목적은 원하는 값을 더 빨리 찾기 위함이다. 즉, 정렬을 했으면 탐색을 해야한다는 의미이다.
순차 탐색
순차탐색은 정렬되지 않은 테이블에서도 사용할 수 있는 가장 직관적인 탐색방법중 하나이다. 리스트롤 for문을 통해 1회 반복하면서 맞는 key가 있다면 반환하는 형태이다.
하지만 다들 알겠지만, O(n)은 그렇게 좋은 시간복잡도가 아니다. 자료가 1억개고 원하는값이 맨 끝에 있다면, 1억번이나 조사해야하는 효율나쁜 탐색법이다.
순차탐색의 구현
def sequential_search(A, key, low, high):
for i in range(low, high + 1):
if A[i] == key:
return i
return None설명이 필요없다
이진 탐색
이진탐색은 정렬된 테이블에서 사용할 수 있는 가장 간단하면서 강력한 탐색방법이다. 리스트를 가운데값을 기준으로 반으로 나눈다. 그 다음 key 값과 비교하면서 더 크다면 가운데값을 위쪽 절반으로, 더 작다면 아래쪽 절반으로 이동하면서 mid = key 가 될 때 까지 탐색하는 방식이다.
n짜리 리스트를 탐색한다고 할 때, n/2 를 반복하는 알고리즘이다. 즉, log(n)만큼의 복잡도를 가진다고 할 수 있다.
이진탐색의 구현
def binary_search(A, key, low, high):
if low <= high:
middle = (low + high) // 2
if key == A[middle]:
return middle
elif key < A[middle]:
return binary_search(A, key, low, middle - 1)
else:
return binary_search(A, key, middle + 1, high)
return Nonerecursion 말고 while문을 통한 구현도 있지만 생략하겠다.
보간 탐색
Interpolation search이다. 이름이 굉장히 생소한 탐색ㅇ인데, 이진탐색의 일종이다. 탐색위치를 현재의 키 값, low, high를 고려하여 탐색위치를 예측하는 방식이다.
예측공식은 다음과 같다.
middle = int(low + (high - low) * (key - A[low]) / (A[high] - A[low]))
나머지는 이진탐색과 동일하다.
보간탐색의 구현
def search_interpolation(A, key, low, high, cnt):
if A(low <= key <= A[high]):
middle = int(low + (high - low) * (key - A[low]) / (A[high] - A[low]))
cnt = cnt + 1
print("middle : %d" % middle)
if key == A[middle]:
return middle
elif key < A[middle]:
return binary_search(A, key, low, middle - 1)
else:
return binary_search(A, key, middle + 1, high)
return None
해싱
우편물을 각 호수별로 구분된 칸에 넣는것처럼, 해싱은 각 탐색키와 래코드 키 값을 비교하는것이 아니라, 키 값을 연산을 이용하여 위치를 계산하여 저장하는 것이다.
우편물을 각각의 칸에 저장하면, 주소만 알면 바로 꺼낼 수 있는 것처럼, 해싱에서도 키를 알면 계산을 통해 주소를 알아낼 수 있고, 주소만 알면 바로 값을 꺼낼 수 있기에 효과적인 방법이라 할 수있다. 다만 수가 너무 많아지면 메모리에 해시를 더 이상 올릴 수 없게 된다.
해싱과 오버플로
해싱은 M개의 버킷(Bucket)으로 이루어진 테이블이고, 버킷은 안에 여러 슬롯을 가진다. 실제로는 그 슬롯에 여러 데이터가 들어가겠지만, 간략하가 하나씩만 들어간다고 가정하자.
오버플로는 해상 버킷의 슬롯보다 많은 데이터가 할당 된 경우 발생하는 현상이다. 이상적인 해싱에서는 충돌이 절대 일어나지 않아야 한다. 따라서 메모리를 늘려야하지만, 무한정 메모리를 늘릴 수는 없다. 이에 오버플로를 처리하는 다양한 방법이 나오게 되었다.
아래의 예시들은 그림으로 보는것이 이해가 더 빠를것이다.
선형 조사법 Linear Probing
식에 따라 주소를 계산하고 삽입을 반복하다가, 만약 충돌이 발생하게 되면, 바로 옆의 버킷으로 이동하면서 비어있는 버킷에 값을 삽입하는 방식이다.
그림으로 보면 다음과 같다.
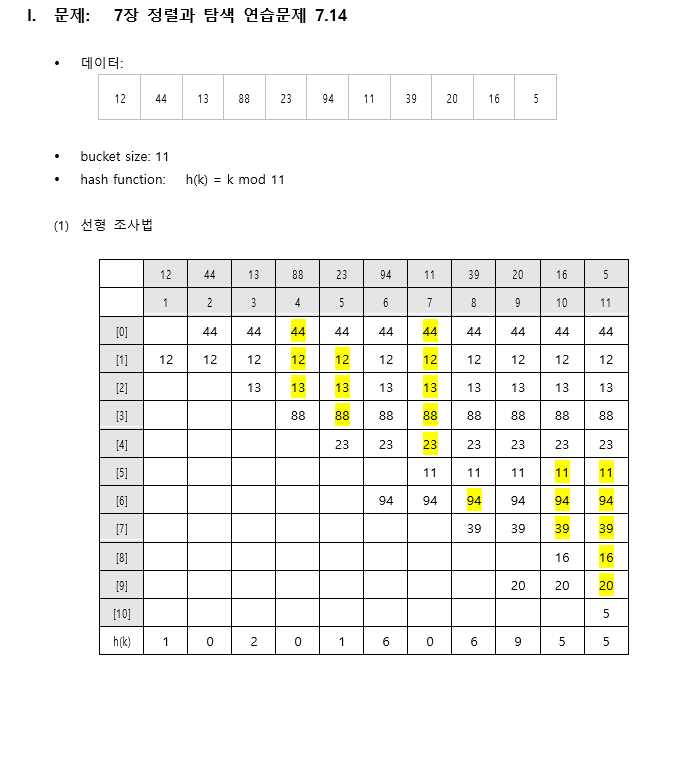
삭제의 경우, 그냥 삭제하고 비워두면, 컴퓨터가 자동적으로 그 다음 값들이 다 비어있다고 판단, 정확한 탐색에 실패할 수 있다. 따라서 visited를 이용하여 해당 해시가 사용 된 적이 있는지 기록해놓고 판단해야 한다.
군집화 Clustering
하지만 이런식으로 한칸씩 미루는 방식으로 값을 추가할 경우, 데이터가 한쪽에 몰리는 군집화, 클러스터링 현상이 발생할 수 있다. 균형있는 데이터가 필요하기에 이러한 문제점을 해결해 주어야 한다.
이차조사법 quadratic probing
군집화 발생을 줄이기 위해, 조사할 다음 위치를 결정하는 식을 변경한다.
식은 다음과 같다
h’(k) = (k + j * j) % 11
이 식을 이용하면 h(k)는 h(k), h(k) + 1, h(k) + 4, h(k) + 9 즉 i의 제곱만큼씩 커진다.
그림으로 보면 다음과 같다.
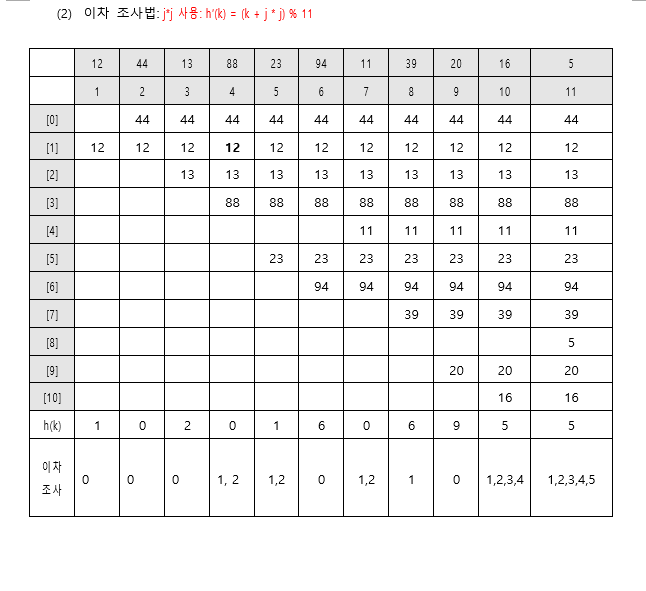
이중 해시법 Double Hashing
재해싱이라고도 불리는 기법이다. 충돌 발생 시 다음 위치를 구할 때, 아예 다른 별도의 해시함수를 사용하는 방식이다
글로는 이해가 잘 가지 않을것이다.
그림으로 보면 다음과 같다
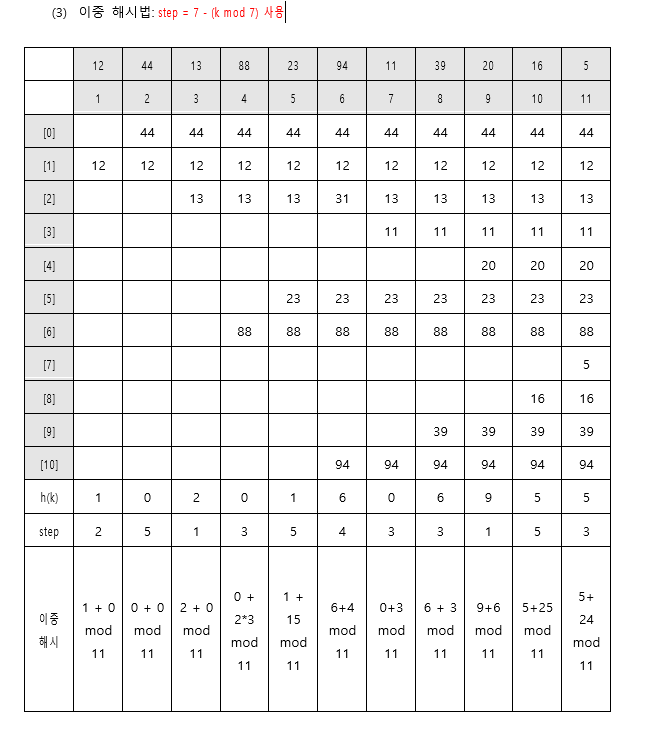
즉, step이라는 특수한 값을 가지고, 충돌이 발생하면 이 값을 i만큼씩 늘려가면서 다음 저장 위치를 찾는 방식이다.
체이닝
연결리스트를 생각하면 쉽다.
만약 충돌이 발생하면 해당 버킷에 링크를 걸어서 다음 값을 넣어주는 방식이다. 하나의 버킷에 여러 레코드를 넣을 수 있다.
