컴퓨터 연산
서론
컴퓨터 워드(word)는 비트로 구성되어 있으므로, 이진수로 표시할 수 있다. 이를 통해 컴퓨터에서 + - * / 가 어떤식으로 실행되는지, 또 실수영역에서는 어떤식으로 실행되는지 알아본다.
Number Systems
The Binary Number
Bit -> 0 or 1
8 bit -> 1 byte
4 byte – 32bit machine
Arithmetic nums 기본적으로 binary
우리가 쓸때는 Decimal -> ASCII
Binary 기반의 연산, 입출력
Ascii 4byte -> 9999
Binary 4bye -> 2^32
따라서 우리는 binary를 사용함
16비트를 32로 확장하면서 변하지 않도록 하는법
MSB에 맞춰서 남은칸을 전부 1 이나 0으로 채움
덧셈과 뺄셈
덧셈
덧셈은 우리가 생각하는 그대로 더하는것으로 실행된다.
0000 0000 0000 0000 0000 0000 0000 0111 = 7 +
0000 0000 0000 0000 0000 0000 0000 0110 = 6
0000 0000 0000 0000 0000 0000 0000 1101 = 13
오른쪽에서 왼족으로 한 비트씩 더하고, 이떄 생기는 올림수(carry)는 바로 왼쪽 자리로 보낸다.
뺄셈
뺄셈은 덧셈을 이용한다.
5-3 = 5 + (-3)인것을 이용하는것이다.
, 뺄 값의 부호를 바꾸어 더하는것이다.
0000 0000 0000 0000 0000 0000 0000 0111 = 7 -
0000 0000 0000 0000 0000 0000 0000 0110 = 6
0000 0000 0000 0000 0000 0000 0000 0001 = 1
혹은, 2의 보수를 이용하여 -6을 더하는 방식으로도 할 수 있다.
0000 0000 0000 0000 0000 0000 0000 0111 = 7 +
1111 1111 1111 1111 1111 1111 1111 1010 = -6
0000 0000 0000 0000 0000 0000 0000 0001 = 1
Singed / Unsigned
unsigned (corresponding to the C declaration unsigned int)
-- 모든 수는 양수이고, MSB의 1이 가장 큰 숫자를 나타냄.
signed (C declaration is signed int or just int)
-- 숫자가 양수 혹은 음수이고, MSB의 1이 그 수가 음수임을 나타냄.
오버플로우
- 제한적인 레지스터의 크기때문에 발생함
- 4bit + 4bit -> 5bit = Carry가 발생했다고 함
- Unsigned number의 경우 last carry가 발생, 숫자의 표현범위를 넘어감
- Signed 의 경우 두개의 부호가 같은 경우 범위를 넘어가 음수 + 음수 -> 양수가 나오거나, 양수 + 양수가 음수가 되거나 함
곱셈
모든 과정에서
- multiplicand 는 shift된다
- multiplier의 다음 비트를 검사한다
- 만약 이 비트가 1이면, Shifted multiplicand는 프로덕트에 더해진다.
곱셉의 하드웨어 구성
데이터가 위에서 아래로 흐르며 계산된다.
multiplier 32비트 miltiplier register에 있고, 64비트 곱 레지스터는 0으로 초기화 되어 있다고 가정하자.
우리가 아는 계산방법대로는, 매 단계마다 multiplicand를 왼쪽으로 한자리씩 이동시키고, 필요하면 중간결과에 더해주는식으로 계산되어야 한다.
이렇게 32단계를 거치면, 32bit multiplicand가 왼쪽으로 32번 이동하게된다. 그러므로 64bit multiplicand register 가 필요하게 된다. 이 레지스터의 오른쪽 절반은 32 bit multiplicand로, 왼쪽 절반은 0으로 초기화된다. 이 레지스터는 64bit multiplication register 에 축적되는 합과 피승수의 위치를 맞추기 위해 매 단계마다 1비트씩 왼쪽자리로 이동된다.
오른쪽 그림에서는 각 비트 연산에 필요한 3단계를 보여준다. multiplier의 LSB(multipler0)은 multiplicand를 곱 레지스터에 더할지 말지를 결정한다.
단계 2에서 왼쪽으로 자리이동하는 것은 종이와 연필로 게산했을 때와 같이 피연산자를 왼쪽으로 이동시키는 역할을 한다.
단계 3에서 오른쪽으로 자리이동하는 이유는 다음 번 반복에서 검사할 승수의다음 비트를 주입하기 위해서이다.
결과를 얻기 위해서는 이러한 단계를 32번 반복해야한다. 각 단계에 한 클럭 사이클이 필요하다면, 이 알고리즘은 32비트 숫자 2개를 곱하는데 거의 100클럭 사이클이 걸린다.
수정된 버전
첫번째 버전과 비교해보면 multiplicand register, ALU, multiplier register는 전부 32bit 이고, 곱 레지스터만이 64bit이다. 이번에는 곱이 오른쪽으로 이동한다.
부호 있는 곱셈
- multiplier와 multiplicand를 양수로 변환하고, 원래의 부호를 기억하는 방법.
- 이 알고리즘은 31번 반복한 후 연산자들의 부호가 서로 다를 때만 곱을 음수로 바꾼다.
더 빠른 곱셈
곱셈을 시작하는 초기에 multiplier 32개의 비트를 한꺼번에 조사하면 multiplicand가 더해져야 하는지 아닌지를 바로 알 수 있다. 그러므로 multiplier의 매 비트마다 32비트 덧셈기를 하나씩 할당하면 더 빠른 곱셈이 가능하다.
이러한 병렬구조를 만들면 32번의 덧셈병렬구조가 형성되고, log(32) = 5 즉, 5번의 덧셈시간만 기다리면 된다.
올림수 저장기(Carry save adder)를 사용하거나 파이프라이닝을 통해 해결할 수 있다.
MIPS에서의 곱셈
Mult $s2, $s3
mfhi $s0 moves the value in hi into $s0
mflo $s1 moves the value in lo into $s1
결과는 $s0 hi(상위) 32비트 / $s1 lo(하위) 32비트 저장함
MIPS는 64비트 곱을 저장할 수 있는 한 쌍의 32비트 레지스터를 별도로 제공한다. 이를 Hi, Lo라 부른다.
부호있는 곱셈과 없는 곱셈을 다루기 위해 MIPS는 mult / multu를 제공한다 (U는 Unsigned). 프로그래머는 mflo(move from lo) 명령어를 이용하여 32비트 정수 곱을 범용 레지스터로 가져올 수 있다.
MIPS 어셈블러는 범용 레지스터 3개를 사용하는 곱하기 의사명령어를 제공한다. 곱을 레지스터에 넣기 위해서 mflo, mfhi를 사용한다.
나눗셈
모든 과정에서
- divisor를 오른쪽으로 shift하고 현 dividend와 비교한다.
- divisor가 더 크다면, 0 을 quotient의 다음 비트로서 shift한다.
• divisor가 더 작다면, 새로운 dividend를 가지기 위해 빼고, quotient의 다음 비트로서 1을 shift한다.
Rem – div = 음수면
rem은 복원하고
Q에 0 추가
Div 오른쪽으로 shift
Rem – div = 양수면
rem 에 0 시프트
Q에 1 추가
Div 오른쪽으로 시프트
나눗셈의 하드웨어 구성
출처
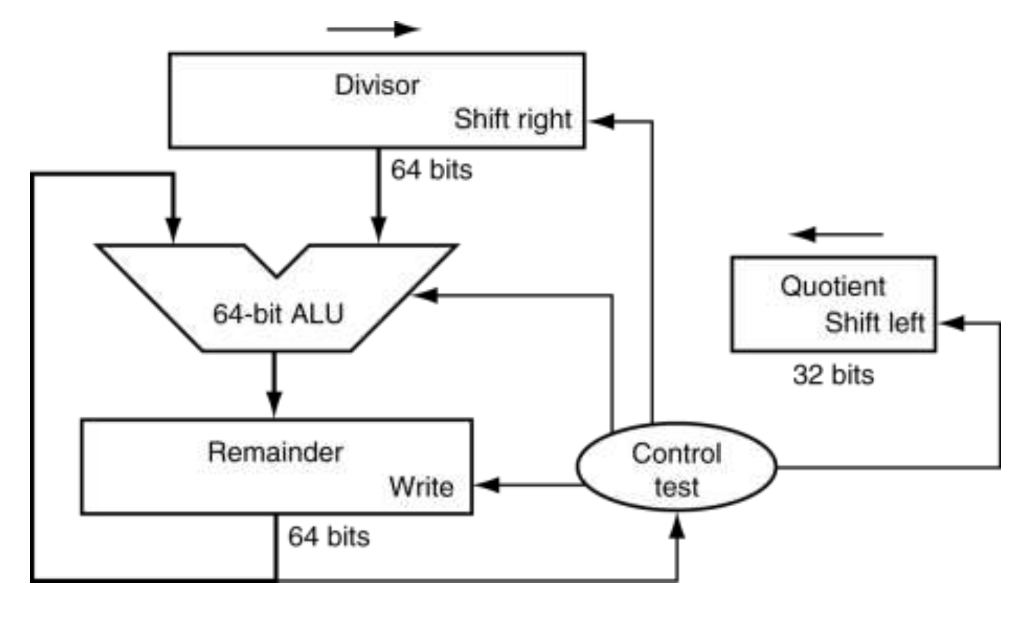
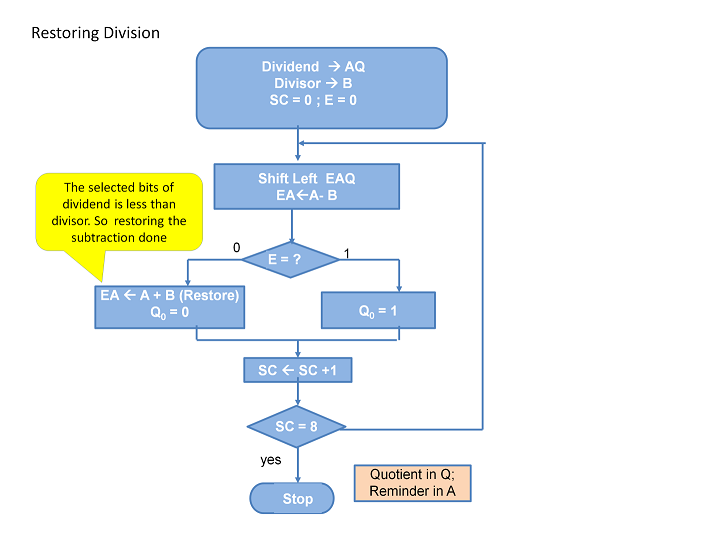
몫 레지스터 32비트를 0으로 초기화 시키고 시작한다. 이 알고리즘은 매번 시작할 때 마다 Divisor 64비트 Divisor 오른쪽으로 한 비트씩 이동해야하므로, Divisor를 64비트 Divisor 레지스터에 왼쪽 절반에 넣고 시작한다. 그리고 Dividend와 자리를 맞추기 위해 반복할 때마다 오른쪽으로 한 비트씩 이동한다. 나머지 레지스터는 Dividend와로 초기화된다.
위의 플로우차트는 알고리즘의 ㄷ3단계를 보여준다.
컴퓨터는 Divisor가 Dividend보다 작다는것을 바로 알 지 못한다. 따라서 먼저 Divisor를 빼야한다.
만약 결과가 양수이면, Divisor >= Dividend이다. 따라서 몫을 1을 넣는다.
만약 결과가 음수이면 Divisor <= Dividend이다. 따라서 divisor를 나머지 레지스터에 다시 더함으로써 원래의 값을 회복하고 몫에는 0을 넣는다.
Divisor는 오른쪽으로 자리이동되고 이 과정을 반복한다.
계산이 완료되면 레지스테어는 나머지와 몫이 남게된다.
부호있는 나눗셈
부호가 있는 나눗셈의 Divisior 와 Dividend 의 부호를 억하고 이 부호들이 달느 경우에는 몫을 음수화 하는것이다.
더 빠른 나눗셈
한꺼번에 몫을 두 비트 이상 만들 수 있는 SRT나눗셈이라는 기술을 이용한다. SRT나눗셈은 여러 개의 몫 비트를 예측한다. Dividend와 나머지 상위 비트들을 이용하여 표를 찾아서 몫을 추측하고, 틀린 추측은 그 후의 단계에서 바로잡는다.
최근 사용되는 방법은 한번에 4비트를 추측하는법이다.
MIPS에서의 나눗셈
왼족이나 오른쪽으로 자리이동 될 수 있는 64비트 레지스터에 덧셈과 뺄셈을 할 수 있는 32비트 ALU만 있으면 된다. MIPS는 32비트 Hi Lo 레지스터를 곱셈과 나눗셈용 64비트 레지스터로 사용한다.
나눗셈 몫이 완료된 후에는 Hi는 나머지를 Lo는 몫을 가진다
MIPS에는 div와 divu를 제공한다 (U는 Unsigned). MIPS어셈블러는 범용 레지스터 3개를 사용하는 나누기 의사명령어를 제공한다. 이 의사명령어는 mflo와 mfhl 명령어를 사용하여 원하는 결과를 범용 레지스터에 넣는다.
Floating Point
소숫점 표현
정수는 정수의 간격이 정해져있음. (4bit)
공간이 정해져있기에, 최대치까지 사칙연산을 할 수 있음
소수점은 이러한 개념이 없고, 한 수가 무한대까지 나갈 수 있음
이에, 소수를 표현하기 위해선, 정규화된 표현방법으로 변화해야함
Fractional Binary Numbers
소수 10을 2진수, 혹은 반대로 가능
Ex)
5 + 3/4 = 5.75 = 5 + 0.5+ 0.25 = 5 + 1/2 + 1/4 + 101 0.1 0.01 -> 101.11(2)
2 + 7/8 10.111(2)
작은수인데도 불구하고 표현이 말도 안된다.
부동소수점 표현
어떤 숫자이건, 일관된 표현 기법으로 함 (근사치로 표현)
Sign(1) exponent(8) fraction(23)
근사치라고는 하지만 정밀한 표현이 가능함
이는 IEEE에서 표준으로 제안한 방식을 따름
(10)^sign F 2^E
ex)
고정소수점 263.3을 부동소수점으로 바꾸면
100000111.010011001100110... 과 같이 표현된다.
이를 맨 앞에 1 바로 뒤에, 소수점을 옮겨서 표현하도록 변환한다. 이러한 과정을 거치면,
1.00000111010011001100110... * 2^8(2의 8승) 으로 변환된다.
2^8은 8을 지수라 하고, exponent 부분에 기록. 다만 이 경우 오류가 날 수 있기에 +127을 한 후 기록해준다.
소수점 이후 전체 숫자열은 fraction 부분(23bit)에 저장한다. 이러한 방식을 따르면
부호 비트(1 bit) : 0 (양수)
지수 비트(8 bit) : 10000111 (127 + 8 = 135)
가수 비트(23 bit) : 00000111010011001100110
이렇게 표현할 수 있다.
이를 변환해보면 매우 0.3과 매우 유사한 수치가 나온다.
Fp addition
기본적으로 지수를 어느 한 방향으로 맞춰야한다
Fp multiplication
Exp 계산 할 때 원래보단 127이 더해진 값이므로, 그냥 더하면 bias가 두번들어감
따라서 bias를 한번 빼 줘야함