볼록 함수에서 극값 or 최대/최소를 찾을 때?
삼분 탐색은 매개 변수 탐색의 일종으로, 이분 탐색과 비슷하다.
차이점은,
📌 이분 탐색 : 단조 증가/감소하는 경우에만 사용 가능
📌 삼분 탐색 : 아래/위로 볼록한 경우(넓은 범위)에도 사용 가능
단, 볼록이 여러 번 반복되는 경우는 삼분 탐색이 불가능하다. (한쪽은 단조 증가, 다른 한쪽은 단조 감소하는 경우만 사용 가능)
💡 삼분 탐색
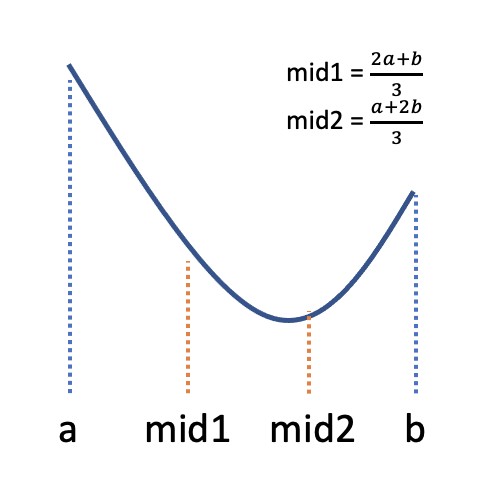
첫 구간의 시작점의 좌표를 a, 끝점의 좌표를 b라고 하자.
최솟값을 구해보자.
- 구간을 삼등분 하는 두 점을 mid1, mid2로 둔다.
- f(mid1) > f(mid2) 일 때 (위의 경우), 구간 [a, mid1] 에는 최솟값이 존재할 수 없다. 따라서 시작점을 mid1으로 옮기고 해당 구간을 제거한 후 구간 [mid1, b]에서 탐색을 진행한다.
- f(mid1) < f(mid2) 일 때, 구간 [mid2, b]에는 최솟값이 존재할 수 없다. 따라서 끝점을 mid2로 옮기고 해당 구간을 제거한 후 [a, mid2]에서 탐색을 진행한다.
- 1~3을 적당한 횟수로 반복한다. (bj11662에서는 100번 반복함)
- 시간복잡도 : O(logN)
📍 구현 (bj11662)
while (T--) {
mid1 = sqrt(pow(m_start_x - g_start_x, 2) + pow(m_start_y - g_start_y, 2)); // mid1은 시작점 사이 거리
mid2 = sqrt(pow(m_end_x - g_end_x, 2) + pow(m_end_y - g_end_y, 2)); // mid2는 끝점 사이 거리
if (mid1 > mid2) { // 시작점을 mid1으로 옮긴다
m_start_x = changeStart(m_start_x, m_end_x);
m_start_y = changeStart(m_start_y, m_end_y);
g_start_x = changeStart(g_start_x, g_end_x);
g_start_y = changeStart(g_start_y, g_end_y);
}
else if (mid1 < mid2) { // 끝점을 mid2로 옮긴다
m_end_x = changeEnd(m_start_x, m_end_x);
m_end_y = changeEnd(m_start_y, m_end_y);
g_end_x = changeEnd(g_start_x, g_end_x);
g_end_y = changeEnd(g_start_y, g_end_y);
}
else {
break;
}
}관련 문제 - 백준 11662번: 민호와 강호
참고 링크 - https://m.blog.naver.com/PostView.nhn?blogId=kks227&logNo=221432986308&proxyReferer=https:%2F%2Fwww.google.com%2F


