소수 찾기 (제곱근, 에라토스테네스의 체)

Maeve·2021년 11월 15일

알고리즘

목록 보기

4/5

1. 기본적인 방법

✅ 소수는 1과 자기자신(N)으로만 나누어떨어진다.

가장 기본적으로 N을 2부터 N-1 까지 나누어 보고, 나누어떨어지지 않으면 소수로 판정한다.

유의할 점은 1은 소수가 아니라는 것이고 예외 처리한다.

시간복잡도 : O(logN)

📍 기본 구현

void isPrime(int num) {
    if (num < 2) return;	// 0, 1 은 소수가 아니다

    for (int i = 2; i < num; i++) {
        if (num % i == 0)
            return;
    }
    ans++;
}

2. 제곱근을 이용한 방법

기본적인 방법과 유사하다.

N을 제곱근까지만 나눈다.

시간복잡도 : O(log(√N)

✅ 제곱근까지만 나눠도 되는 이유

N = A × B 라고 하자.
1 ≤ A, B < N 이 성립한다.

만약 A, B 가 N의 제곱근보다 커지면 모순이 발생한다.

if A, B > sqrt(N)
then, A × B > N

따라서, A 와 B 중 적어도 하나는 N의 제곱근 보다 작거나 같다.

📍 제곱근을 이용한 구현 (i * i <= num)

void isPrime(int num) {
    if (num < 2) return;

    for (int i = 2; i * i <= num; i++) {
        if (num % i == 0)
            return;
    }
    ans++;
}

3. 에라토스테네스의 체

✅ 숫자가 커지면 어떻게 해야 할까? - 에라토스테네스의 체

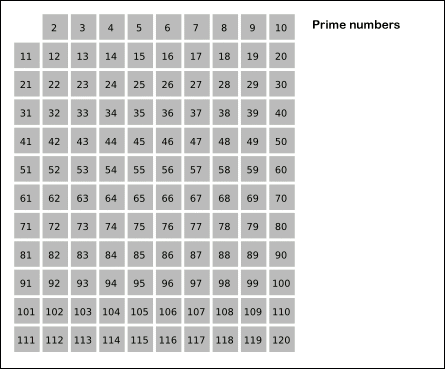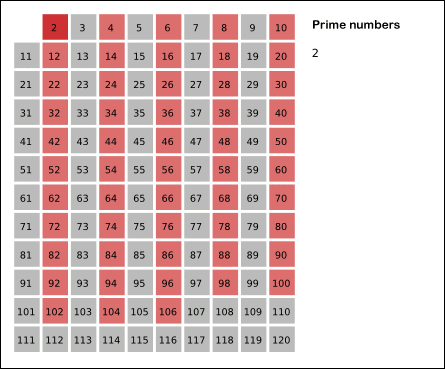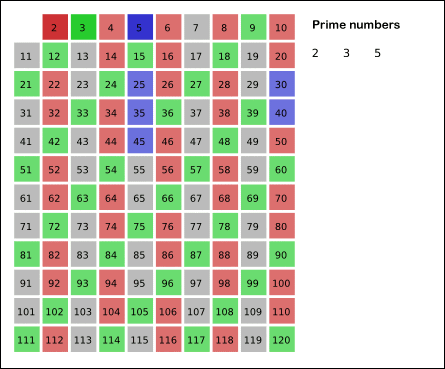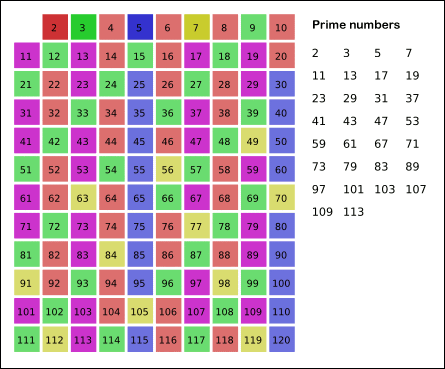
배열을 선언한 후 1로 채운다. (i로 채워도 상관x)

2부터 배수를 지워나간다.

남은 prime[i] = 1 인 i 들이 소수이다.

시간복잡도: O(Nlog(logN))

📍 에라토스테네스의 체 구현

for (int i = 2; i <= n; i++) {
    prime[i] = 1;	// 배열을 1로 채운다 
}

for (int i = 2; i * i <= n; i++) {
    if (prime[i] == 0)
        continue;
    
    for (int j = 2; i * j <= n; j++) {
        prime[i * j] = 0;	// 배수를 0으로 바꾼다 
    }
}	
// 1로 남은 수들이 소수이다