✅ 0은 2와 5의 곱으로 만들어진다.

처음 백준 1676번: 팩토리얼 0의 개수을 풀 때는 팩토리얼 함수를 구현해서 연산을 하고, 문자열로 바꾼 후 뒤에서 부터 문자를 세려고 했다. 하지만 결과는 실패. 500!의 경우 숫자가 매우 크다.
검색을 해보니 팩토리얼 계산을 할 필요가 없는 문제였다.
0은 2 × 5 로 만들어지므로, N까지 2와 5의 개수를 센 후 작은 값이 정답이다.
✅ 2와 5중 어느 것이 더 많을까?
하지만 조금 더 생각해보면, 2는 5보다 작은 수여서 소인수분해 결과 자연스럽게 5의 개수가 훨씬 적어지게 된다. 따라서 0의 개수는 1부터 N까지 수에 포함된 5의 개수를 세면 된다.
(물론, 2와 5의 개수를 센 후 작은 값을 답으로 하는 것이 일반적인 방식이다.)
구현 시 주의할 점은 25, 125 와 같은 5의 제곱수는 5를 여러 개 포함하고 있어 이를 처리해줘야 한다.
📍 구현 (bj1676)
[1]
while (n >= 5) {
cnt += n / 5;
n /= 5;
}
단순히 5로 나누지 않고, 반복문을 통해 5로 나누며 누적값을 구한다.
[2]
for (int i = 1; i <= n; i++) {
int num = i;
while (num % 5 == 0) { // 5로 나눠떨어질 때만 고려
num /= 5;
cnt++;
}
}[3] 일반적인 경우 - 2, 5 모두 고려
int main() {
int n;
int two = 0;
int five = 0;
cin >> n;
for (int i = 2; i <= n; i *= 2) {
two += n / i;
}
for (int i = 5; i <= n; i *= 5) {
five += n / i;
}
// two, five 중에 작은 값이 정답
if (two > five) cout << five;
else cout << two;
}✅ 일반적인 경우를 보자
백준 2004번: 조합 0의 개수도 위와 비슷한 문제이다.
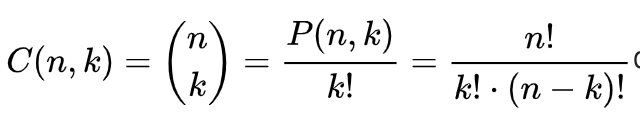
n, k, (n-k) 에 대해 각각 2와 5의 개수를 구하고,
2와 5 중 "n!일 때 개수 - (k!일 때 개수 + (n-k)!일 때 개수)" 가 작은 값이 정답이다.
📍 구현 (bj2004)
pair<long long, long long> getZero(long long n) {
long long two = 0, five = 0;
for (long long i = 2; i <= n; i *= 2) two += n / i;
for (long long i = 5; i <= n; i *= 5) five += n / i;
return (pair<long long, long long> (two, five));
}정수의 범위를 고려해서 long long 자료형을 써야 한다.
관련 문제 - 백준 1676번: 팩토리얼 0의 개수, 백준 2004번: 조합 0의 개수
참고 링크 - https://st-lab.tistory.com/165, https://sihyungyou.github.io/baekjoon-1676/,

