AVL 트리는 자가 균형을 맞추는 이진 탐색 트리의 한 종류로, 다음과 같은 이유로 사용됩니다:
-
균형 유지: AVL 트리는 노드가 추가되거나 삭제될 때마다 트리의 균형을 자동으로 재조정합니다. 이를 통해 트리의 높이를 최소한으로 유지하며, 이는 검색, 삽입, 삭제 작업의 효율성을 보장합니다.
-
일관된 성능 보장: AVL 트리는 균형을 유지함으로써 최악의 경우에도 O(log n)의 시간 복잡도를 보장합니다. 이는 이진 탐색 트리가 한쪽으로 치우친 경우보다 더 나은 성능을 의미합니다.
-
효율적인 검색 연산: 균형이 잘 맞춰진 트리 구조 덕분에 AVL 트리는 빠른 검색 연산을 제공합니다. 이는 대량의 데이터를 다루는 애플리케이션에서 중요한 이점이 될 수 있습니다.
-
순서대로 데이터 접근 가능: AVL 트리는 이진 탐색 트리의 모든 장점을 가지며, 중위 순회를 통해 데이터를 정렬된 순서로 접근할 수 있습니다.
-
동적 데이터 집합에 적합: 데이터가 지속적으로 변경되는 동적인 환경에서 AVL 트리는 트리의 균형을 유지하면서 효과적으로 작동합니다.
그러나 AVL 트리의 단점으로는 삽입이나 삭제 연산시 빈번한 회전이 필요하다는 점이 있습니다. 이는 연산의 복잡도를 증가시키며, 특히 삽입과 삭제가 빈번한 애플리케이션에서는 성능 저하의 원인이 될 수 있습니다. 이러한 경우, 회전을 덜 필요로 하는 다른 자가 균형 이진 탐색 트리 구조, 예를 들어 레드-블랙 트리를 사용하는 것이 더 효율적일 수 있습니다.
AVL 트리는 자가 균형 이진 탐색 트리(self-balancing binary search tree)의 한 종류로, 1962년에 Georgy Adelson-Velsky와 Evgenii Landis에 의해 고안되었습니다. AVL 트리의 주된 목적은 이진 탐색 트리의 성능 저하를 방지하기 위해 트리의 높이를 자동으로 조절하는 것입니다.
AVL 트리의 특징
-
균형 조건: AVL 트리에서는 어떤 노드의 두 자식 서브트리의 높이 차이가 최대 1이어야 합니다. 이를 '균형 조건'이라고 합니다.
-
회전 연산: 균형이 깨졌을 때, AVL 트리는 회전 연산을 통해 균형을 재조정합니다. 이러한 회전에는 단일 회전(single rotation)과 이중 회전(double rotation)이 있습니다.
- 단일 회전: LL 회전(왼쪽 서브트리의 왼쪽에 삽입으로 인한 불균형)과 RR 회전(오른쪽 서브트리의 오른쪽에 삽입으로 인한 불균형)이 여기에 해당합니다.
- 이중 회전: LR 회전(왼쪽 서브트리의 오른쪽에 삽입으로 인한 불균형)과 RL 회전(오른쪽 서브트리의 왼쪽에 삽입으로 인한 불균형)이 여기에 해당합니다.
-
시간 복잡도: AVL 트리에서 삽입, 삭제, 검색 연산은 모두 O(log n) 시간 복잡도를 가집니다.
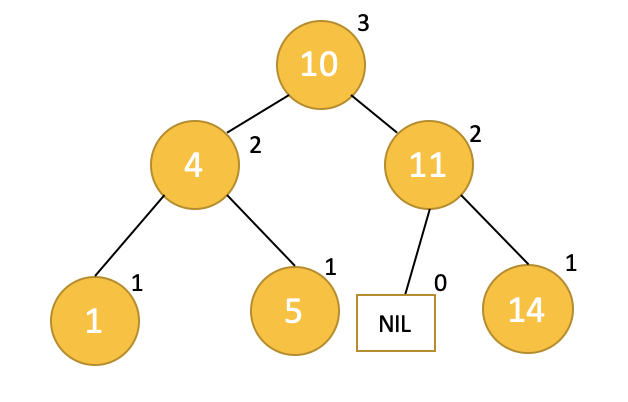
이 그림은 이진 탐색 트리(Binary Search Tree, BST)를 나타내고 있습니다. 각 노드에는 크게 두 가지 정보가 표시되어 있습니다: 노드에 저장된 값(큰 글씨)과 노드의 높이 또는 깊이(작은 글씨).
트리의 루트 노드는 '10'이며, 이 노드의 높이는 '3'입니다. 루트 노드의 왼쪽 자식 노드는 '4', 오른쪽 자식 노드는 '11'입니다. 노드 '4'의 왼쪽 자식은 '1', 오른쪽 자식은 '5'이며, 노드 '11'의 오른쪽 자식은 '14'입니다. 노드 '5'는 왼쪽 자식이 없음을 나타내는 'NIL' 노드를 가지고 있습니다. 각 노드의 높이는 자신을 루트로 하는 서브트리의 높이를 나타내며, 이는 AVL 트리에서 중요한 균형 지표입니다.
해당 트리는 AVL 트리의 조건을 만족하는지 판단하기 위해 각 노드의 높이 정보를 사용합니다. AVL 트리에서는 어떤 노드의 두 자식 서브트리 간 높이 차이가 1 이하가 되어야 합니다. 이 그림에서는 각 노드의 높이가 그 노드의 자식 노드 높이에 기반하여 계산되며, 높이 차이가 1 이하인지를 확인할 수 있습니다.
그림의 형태로 보았을 때, 모든 노드가 AVL 트리의 균형 조건을 만족하는 것처럼 보입니다. 예를 들어, 루트 노드 '10'의 왼쪽과 오른쪽 서브트리의 높이 차이는 1 (3-2), 노드 '4'의 서브트리 높이 차이는 1 (2-1) 등으로 모두 1 이하입니다.
특징
-
균형 상태: 모든 노드에서 왼쪽과 오른쪽 자식 노드의 높이 차이가 1 이하입니다. 이는 AVL 트리의 균형 조건을 만족함을 나타냅니다.
-
서브트리 높이: 각 노드의 작은 숫자는 해당 노드를 루트로 하는 서브트리의 높이를 나타냅니다. 높이는 그 노드로부터 가장 깊은 리프(잎) 노드까지의 가장 긴 경로의 길이입니다.
-
NIL 노드: 'NIL'은 해당 위치에 자식 노드가 없음을 나타내는 표시입니다. 컴퓨터 과학에서 트리의 끝을 표시하기 위해 사용되며, NULL이라고도 합니다. 이는 트리 구조에서 끝을 나타내는 특별한 종류의 노드로, 실제 값을 저장하지 않고, 자식이 없는 노드의 자리를 차지합니다.
이 트리는 AVL 트리가 유지해야 하는 균형 상태를 잘 보여주며, 각 노드의 높이를 통해 이 균형 상태를 유지하기 위한 회전 연산의 필요성을 판단할 수 있습니다. 그림에 제시된 트리는 현재 균형이 잘 맞춰진 상태로 보이며, 추가적인 회전 연산 없이도 AVL 트리로서의 조건을 만족하는 것으로 보입니다.
물론입니다. AVL 트리는 Adelson-Velskii와 Landis에 의해 개발된 자가 균형 이진 탐색 트리입니다. AVL 트리는 삽입, 삭제, 검색 작업을 효율적으로 수행하기 위해 트리의 높이 균형을 유지합니다.
다음은 AVL 트리를 구현하는 자바스크립트 코드 예시입니다. 이 코드는 AVL 트리의 기본적인 구조와 삽입, 회전 로직을 포함하고 있습니다. 주석을 달아 이해를 돕도록 하겠습니다.
class Node {
constructor(data) {
this.data = data; // 노드의 데이터
this.height = 1; // 노드의 높이
this.left = null; // 왼쪽 자식 노드
this.right = null; // 오른쪽 자식 노드
}
}
class AVLTree {
constructor() {
this.root = null; // AVL 트리의 루트 노드
}
// 노드의 높이를 반환하는 함수
getHeight(node) {
if (!node) return 0;
return node.height;
}
// 노드의 균형 인수(balance factor)를 계산하는 함수
getBalanceFactor(node) {
if (!node) return 0;
return this.getHeight(node.left) - this.getHeight(node.right);
}
// 오른쪽 회전 함수
rightRotate(y) {
let x = y.left;
let T2 = x.right;
// 회전
x.right = y;
y.left = T2;
// 높이 업데이트
y.height = Math.max(this.getHeight(y.left), this.getHeight(y.right)) + 1;
x.height = Math.max(this.getHeight(x.left), this.getHeight(x.right)) + 1;
return x;
}
// 왼쪽 회전 함수
leftRotate(x) {
let y = x.right;
let T2 = y.left;
// 회전
y.left = x;
x.right = T2;
// 높이 업데이트
x.height = Math.max(this.getHeight(x.left), this.getHeight(x.right)) + 1;
y.height = Math.max(this.getHeight(y.left), this.getHeight(y.right)) + 1;
return y;
}
// AVL 트리에 노드를 삽입하는 함수
insertNode(node, data) {
// 기본 이진 탐색 트리 삽입
if (!node) return new Node(data);
if (data < node.data) {
node.left = this.insertNode(node.left, data);
} else if (data > node.data) {
node.right = this.insertNode(node.right, data);
} else {
return node; // 중복된 값은 삽입하지 않음
}
// 노드의 높이 업데이트
node.height = 1 + Math.max(this.getHeight(node.left), this.getHeight(node.right));
// 균형 인수 가져오기
let balanceFactor = this.getBalanceFactor(node);
// 균형 상태가 아닐 경우 4가지 경우의 수를 확인하고 회전
// Left Left Case
if (balanceFactor > 1 && data < node.left.data) {
return this.rightRotate(node);
}
// Right Right Case
if (balanceFactor < -1 && data > node.right.data) {
return this.leftRotate(node);
}
// Left Right Case
if (balanceFactor > 1 && data > node.left.data) {
node.left = this.leftRotate(node.left);
return this.rightRotate(node);
}
// Right Left Case
if (balanceFactor < -1 && data < node.right.data) {
node.right = this.rightRotate(node.right);
return this.leftRotate(node);
}
return node;
}
// AVL 트리에 데이터 삽입을 위한 함수
insert(data) {
this.root = this.insertNode(this.root, data);
}
// (옵션) AVL 트리의 내용
을 출력하는 함수
printTree(node = this.root, space = 0, height = this.root.height) {
if (!node) return;
space += height;
this.printTree(node.right, space);
console.log(" ".repeat(space - height) + `${node.data}`);
this.printTree(node.left, space);
}
}
// AVL 트리 사용 예
let tree = new AVLTree();
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(40);
tree.insert(50);
tree.insert(25);
// 트리 출력
tree.printTree();이 코드는 AVL 트리를 생성하고, 삽입 및 회전 로직을 포함하고 있습니다. insert 메소드를 사용하여 트리에 데이터를 삽입하고, printTree 메소드를 사용하여 트리의 구조를 콘솔에 출력할 수 있습니다.
AVL 트리의 활용
AVL 트리는 균형이 잘 유지되는 특성 덕분에 이진 탐색 트리에서 발생할 수 있는 성능 저하 문제를 효과적으로 해결합니다. 따라서, AVL 트리는 데이터베이스 시스템, 파일 시스템, 메모리 관리 시스템 등에서 효율적인 데이터 검색과 관리에 널리 사용됩니다.
면접 질문 예시
AVL 트리와 관련된 면접 질문은 다음과 같은 형태로 나타날 수 있습니다:
-
AVL 트리의 균형 조건이란 무엇인가요?
- 이 질문은 AVL 트리의 기본적인 균형 유지 메커니즘을 이해하고 있는지를 평가합니다.
-
AVL 트리에서 회전 연산이란 무엇이며, 어떻게 작동하나요?
- 이 질문은 트리의 균형을 재조정하는 회전 기법에 대한 이해를 확인합니다.
-
AVL 트리와 일반 이진 탐색 트리의 차이점은 무엇인가요?
- 이 질문은 AVL 트리의 자가 균형 특성과 이진 탐색 트리와의 차이점을 이해하고 있는지를 평가합니다.
