이진 탐색 트리(Binary Search Tree, BST)를 사용하는 주된 이유는 데이터의 효율적인 정렬, 검색, 삽입, 삭제를 가능하게 하는 그 구조에 있습니다. BST는 다음과 같은 이유로 널리 사용됩니다:
-
정렬된 데이터의 효율적인 검색: BST는 평균 O(log n)의 시간 복잡도로 데이터를 검색할 수 있습니다. 이는 트리가 균형잡힌 경우에 해당하며, 데이터가 정렬된 상태에서 이진 탐색을 수행하는 것과 유사합니다.
-
동적 데이터 집합 관리: BST는 데이터가 계속 추가되거나 삭제되는 동적인 환경에서도 효과적입니다. 삽입과 삭제 역시 평균적으로 O(log n)의 시간 복잡도를 가집니다.
-
중위 순회를 통한 정렬된 데이터 접근: BST의 중위 순회(in-order traversal)는 항상 정렬된 순서로 데이터에 접근하게 해줍니다. 이는 정렬된 데이터를 순차적으로 처리해야 하는 경우에 유용합니다.
-
범위 탐색 및 순차 접근 용이: BST는 특정 범위의 데이터를 빠르게 검색하고, 범위 내의 데이터를 효율적으로 순차적으로 탐색하는 데 적합합니다.
-
유연한 구조: BST는 노드의 삽입과 삭제가 비교적 간단하며, 트리의 구조를 유연하게 변경할 수 있습니다.
-
메모리 효율성: 각 노드는 자신의 데이터와 두 개의 자식에 대한 참조만을 가지므로, 메모리 사용이 효율적입니다.
그러나 BST의 성능은 트리의 균형 상태에 크게 의존합니다. 예를 들어, 트리가 한쪽으로 치우쳐있는 경우(예: 링크드 리스트처럼 길게 늘어선 경우), 검색, 삽입, 삭제의 시간 복잡도는 최악의 경우 O(n)이 될 수 있습니다. 이를 해결하기 위해 AVL 트리나 레드-블랙 트리와 같은 자가 균형 이진 탐색 트리(self-balancing binary search tree)가 개발되었습니다. 이러한 구조는 추가적인 로직을 통해 트리가 어느 한쪽으로 치우치지 않도록 유지합니다.
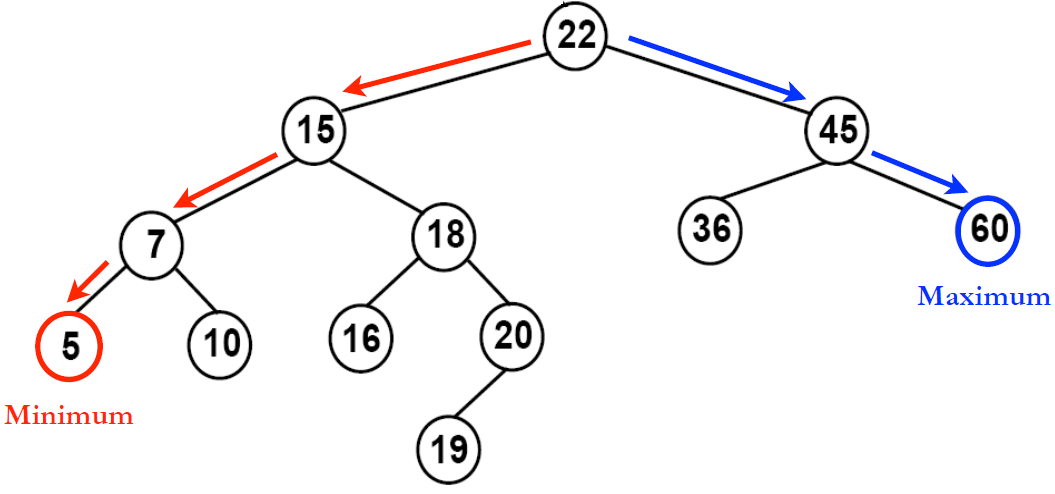
이진 탐색 트리(Binary Search Tree, BST)는 이진 트리(binary tree)의 일종으로, 다음과 같은 특징을 가진 자료 구조입니다.
이 이미지는 이진 탐색 트리(Binary Search Tree, BST)를 나타냅니다. 이진 탐색 트리는 각 노드가 최대 두 개의 자식을 가지며, 왼쪽 자식은 부모 노드보다 작은 값을, 오른쪽 자식은 부모 노드보다 큰 값을 가집니다. 이러한 속성으로 인해 BST에서 데이터를 효율적으로 검색, 삽입, 삭제할 수 있습니다.
이미지에서 빨간색으로 표시된 경로는 트리에서 가장 작은 값을 가진 노드로 가는 경로를 나타냅니다. 이 경우 가장 작은 값은 5이며, 이를 'Minimum'이라고 표시했습니다.
파란색으로 표시된 경로는 트리에서 가장 큰 값을 가진 노드로 가는 경로를 나타냅니다. 이 경우 가장 큰 값은 60이며, 이를 'Maximum'이라고 표시했습니다.
또한, 이진 탐색 트리에서 노드를 찾거나 거쳐가는 경로는 루트 노드에서 시작하여 왼쪽 또는 오른쪽 자식을 거치면서 내려갑니다. 이 트리에서 루트 노드는 15이며, 이 노드를 기준으로 왼쪽 서브트리는 모두 15보다 작은 값을, 오른쪽 서브트리는 모두 15보다 큰 값을 가집니다.
그림에서 볼 수 있듯이, 22의 왼쪽 자식은 15로, 22보다 작으며, 22의 오른쪽 자식은 45로, 22보다 큽니다. 이는 BST의 기본 원칙을 따르고 있음을 보여줍니다.
이진 탐색 트리의 특징
-
정렬된 순서: 각 노드는 키를 가지며, 이진 탐색 트리의 모든 노드는 다음과 같은 순서 속성을 만족합니다:
- 모든 왼쪽 자식 노드들의 키는 해당 노드의 키보다 작습니다.
- 모든 오른쪽 자식 노드들의 키는 해당 노드의 키보다 큽니다.
- 각 서브트리도 이진 탐색 트리입니다.
-
이진 트리: 각 노드는 최대 두 개의 자식(왼쪽과 오른쪽)을 가질 수 있습니다.
-
탐색 효율성: 이진 탐색 트리는 탐색, 삽입, 삭제 등의 연산을 평균적으로 O(log n) 시간에 수행할 수 있습니다. 여기서 n은 트리에 있는 노드의 수입니다. 그러나 트리가 균형을 잃어 선형 구조와 같아진 최악의 경우, 이러한 연산들의 시간 복잡도는 O(n)이 될 수 있습니다.
이진 탐색 트리의 연산
-
삽입(Insertion): 새로운 노드를 삽입할 때, 트리를 루트부터 시작하여 노드의 키를 비교하면서 내려갑니다. 삽입할 키가 현재 노드의 키보다 작으면 왼쪽으로, 크면 오른쪽으로 이동하여 적절한 위치에 새 노드를 삽입합니다.
-
검색(Search): 특정 키를 가진 노드를 찾을 때, 트리를 루트부터 시작하여 키를 비교하면서 내려갑니다. 찾는 키가 현재 노드의 키보다 작으면 왼쪽으로, 크면 오른쪽으로 이동하여 원하는 키를 가진 노드를 찾습니다.
-
삭제(Deletion): 특정 키를 가진 노드를 삭제할 때, 세 가지 경우를 고려해야 합니다:
- 단말 노드(leaf node): 자식이 없는 노드는 간단히 제거할 수 있습니다.
- 한 개의 자식을 가진 노드: 자식을 가진 쪽으로 부모 노드를 연결한 후, 해당 노드를 제거합니다.
- 두 개의 자식을 가진 노드: 후계자 노드(successor node, 보통 오른쪽 서브트리에서 가장 작은 노드) 또는 전임자 노드(predecessor node, 보통 왼쪽 서브트리에서 가장 큰 노드)를 찾아 해당 노드의 위치로 이동시킨 후, 원래 노드를 제거합니다.
이진 탐색 트리의 활용
이진 탐색 트리는 데이터베이스 관리 시스템, 파일 시스템, 탐색 알고리즘 등 다양한 분야에서 데이터를 효율적으로 관리하고 검색하는 데 사용됩니다. 특히, 데이터의 범위 검색(range search)이나 정렬된 데이터의 순회에 유용합니다.
이진 탐색 트리(Binary Search Tree, BST)를 자바스크립트로 구현하는 예시 코드와 각 부분에 대한 주석, 그리고 이진 탐색 트리의 활용 및 면접 질문 예시를 제공하겠습니다.
자바스크립트로 구현한 이진 탐색 트리 예시
class Node {
constructor(data) {
this.data = data; // 노드가 저장할 데이터
this.left = null; // 왼쪽 자식 노드를 가리키는 포인터
this.right = null; // 오른쪽 자식 노드를 가리키는 포인터
}
}
class BinarySearchTree {
constructor() {
this.root = null; // 트리의 루트 노드
}
// 새 노드 삽입
insert(data) {
const newNode = new Node(data);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
// 노드 삽입 도우미 함수
insertNode(node, newNode) {
if (newNode.data < node.data) { // 새 데이터가 현재 노드 데이터보다 작은 경우
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else { // 새 데이터가 현재 노드 데이터보다 큰 경우
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
// 노드 검색
search(node, data) {
if (node === null) {
return null;
} else if (data < node.data) {
return this.search(node.left, data);
} else if (data > node.data) {
return this.search(node.right, data);
} else {
return node;
}
}
// (여기에 더 많은 메소드를 추가할 수 있습니다: 순회, 삭제 등)
}
// 사용 예시
const bst = new BinarySearchTree();
bst.insert(15);
bst.insert(25);
bst.insert(10);
bst.insert(7);
bst.insert(22);
bst.insert(17);
bst.insert(13);
bst.insert(5);
bst.insert(9);
bst.insert(27);
let node = bst.search(bst.root, 7);
console.log(node); // 7을 포함하는 노드 출력이진 탐색 트리의 활용
이진 탐색 트리는 데이터 정렬, 검색 및 관리에 매우 유용합니다. 주요 활용 분야는 다음과 같습니다:
- 데이터베이스: 효율적인 검색, 삽입, 삭제를 위해 데이터베이스 시스템에서 널리 사용됩니다.
- 탐색 알고리즘: 범위 검색이나 정렬된 데이터의 순차적 처리에 유리합니다.
- 파일 시스템: 디렉토리 및 파일 구조를 관리하는 데 사용될 수 있습니다.
면접 질문 예시
이진 탐색 트리와 관련된 면접 질문은 다음과 같은 형태로 나타날 수 있습니다:
-
이진 탐색 트리의 작동 원리는 무엇인가요?
- 이 질문은 이진 탐색 트리의 기본 개념과 속성을 이해하고 있는지를 평가합니다.
-
이진 탐색 트리에서의 삽입과 검색 과정을 설명해주세요.
- 이 질문은 삽입과 검색 알고리즘에 대한 구체적인 이해를 확인합니다.
-
이진 탐색 트리와 균형 이진 탐색 트리의 차이점은 무엇인가요?
- 이 질문은 이진 탐색 트리와 AVL 트리나 레드-블랙 트리 같은 균형 이진 탐색 트리의 차이점을 이해하고 있는지를 평가합니다.
-
이진 탐색 트리에서 삭제 과정은 어떻게 진행되나요?
- 이 질문은 이진 탐색 트리에서 노드를 삭제하는 방법과 관련된 알고리즘을 이해하고 있는지를 평가합니다.
