자료구조
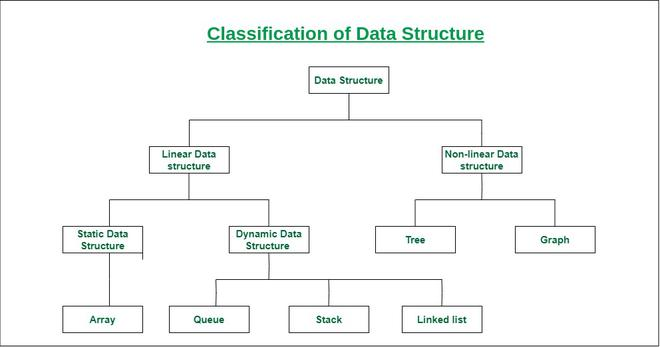
내장형(primitive) 자료형(int, char)이 있고 사용자가 라이브러리를 사용하여 정의하는 참조(non-primitive) 자료형(Array, Queue)이 있습니다. 선형 자료구조와 비선형 자료구조는 데이터 요소들 사이의 관계에 따라 구분됩니다.
선형 자료구조: 데이터 요소들 간의 관계가 일렬로 연결된 형태입니다. 즉, 데이터 요소가 선(line)처럼 일렬로 연결되어 있습니다. 대표적인 예시로는 배열, 연결 리스트, 스택, 큐 등이 있습니다.
비선형 자료구조: 데이터 요소들 간의 관계가 일렬로 연결되어 있지 않은 형태입니다. 즉, 데이터 요소가 선이 아닌 트리, 그래프 등의 형태로 연결되어 있습니다. 대표적인 예시로는 이진 트리, 이진 탐색 트리, 그래프 등이 있습니다.
정적 자료구조: 미리 정해진 크기의 메모리 공간에 데이터를 저장하는 방식입니다. 한 번 크기를 정하면 변경할 수 없으며, 배열이 대표적인 예시입니다.
동적 자료구조: 데이터가 저장될 때 필요한 메모리 공간을 동적으로 할당하고 사용하는 방식입니다. 필요할 때마다 메모리를 할당하고 해제할 수 있으며, 연결 리스트, 힙 등이 대표적인 예시입니다. 동적 자료구조는 정적 자료구조와 달리 메모리를 효율적으로 사용할 수 있으며, 데이터의 크기에 따라 유연하게 대처할 수 있습니다
cf) 정적 할당: 컴파일 시점에 변수나 객체가 필요한 메모리 공간을 할당하는 방식입니다. 메모리 사용량이 고정되어 있어, 크기를 변경할 수 없습니다. 변수의 유효 범위가 제한되며, 전역 변수의 경우 프로그램이 종료될 때까지 메모리를 차지하게 됩니다.
동적 할당: 프로그램 실행 중에 필요한 메모리 공간을 할당하는 방식입니다. 메모리 사용량이 동적으로 변경될 수 있습니다. 메모리 공간을 할당하고 해제하는 데 자원이 들지만, 유연성이 높아서 메모리 효율을 높일 수 있습니다.
Array
배열이란 같은 성질을 갖는 항목들의 집합입니다. 같은 특성을 갖는 원소들이 순서대로 구성된 집합으로 선형 자료 구조입니다. 순차적으로 저장된 데이터를 참조하는 데에는 Index가 사용됩니다.
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Data | 3 | 5 | 1 | 7 | 9 |
2차원 배열
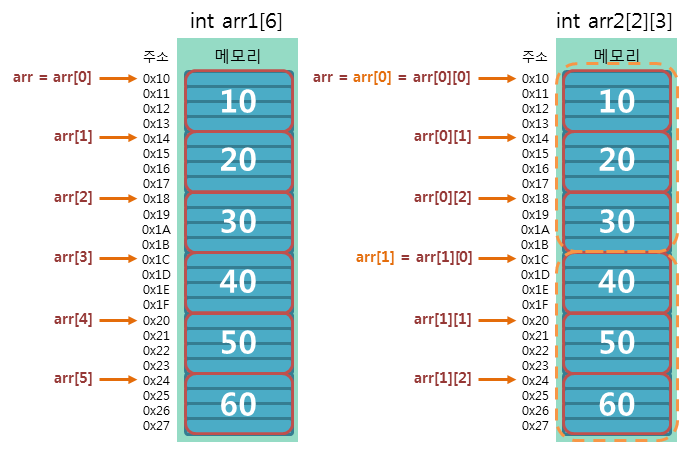
2차원 배열은 1차원 배열을 여러 개 묶어서 구성한 자료 구조입니다. 1차원 배열이 데이터를 일렬로 나열한 구조라면, 2차원 배열은 데이터를 격자 형태로 나열한 구조입니다. 2차원 배열은 일반적으로 행(row)과 열(column)의 형태를 갖고 있습니다. 각 행과 열은 1차원 배열을 형성하며, 행과 열을 결합하여 전체적인 2차원 배열을 구성합니다.
2차원 배열의 각 원소(element)는 행과 열의 인덱스를 이용하여 접근할 수 있습니다. 예를 들어, 2차원 배열 arr의 3행 4열에 있는 원소에 접근하려면 arr[2][3]과 같이 행과 열의 인덱스를 사용합니다. 이때, 배열의 인덱스는 0부터 시작하므로 3행 4열은 각각 2와 3으로 인덱싱됩니다. 2차원 배열은 주로 행렬(matrix) 연산에서 사용되며, 데이터를 격자 형태로 처리해야 할 경우에도 유용합니다.
원소 확인 및 변경
위의 배열에서 인덱스 3에 있는 7이란 데이터를 8로 변경한다고 하면, 인덱스 3을 찾는 방법은, 배열은 메모리 상에 일렬로 나열되어 있으니 배열의 시작 주소인 인덱스 0에서 3번째 칸을 찾으면 됩니다. 이는 시작 주소+ 3으로 O(1)만에 찾고, 변경할 수 있습니다. 
원소 삽입 및 삭제
인덱스 3에 있는 데이터를 삭제하여도, 배열은 메모리 상에 일렬로 나열되어있고, 크기는 고정되어있다는 특징을 가지기 때문에 인덱스 3은 그대로 있고 우측에 데이터들이 한 칸씩 당겨집니다. 인덱스 3 뒤에 있는 3 개의 원소를 한 칸씩 당겨야 합니다. 만약 인덱스 0의 데이터를 삭제한다고 하면, 6개의 원소를 한 칸 당겨야 하고, 인덱스 6의 데이터를 삭제한다고 하면 0개의 원소를 한 칸 앞으로 이동시킵니다. 평균적으로 어떠한 원소를 삭제할 때 N(배열의 크기)/2만큼 땡겨야 하므로 삭제의 시간 복잡도는 O(N)이 됩니다.

삽입도 마찬가지로 O(N)입니다. 크기가 10인 배열에 7개의 데이터가 들어가 있다고 면, 인덱스 3 위치에 데이터 19를 추가한다고 했을 때, 인덱스 3 우측에 있는 데이터들이 한 칸씩 우측으로 밀려납니다.

List
데이터 요소를 연속된 메모리 공간에 저장하지 않고, 각각의 데이터 요소가 다음 요소의 주소를 가리키는 방식으로 구현됩니다. 이러한 구조로 인해 데이터 요소의 추가나 삭제가 용이합니다. ArrayList는 내부적으로 배열을 사용하며, LinkedList는 각 요소를 연결한 구조를 사용합니다.
원소 확인 및 변경(LinkedList)
'소'를 '닭'으로 바꾼다고 하면, 순차 접근 방식을 사용하기 때문에 처음부터 순차적으로 탐색해서 '소'를 찾아야만 합니다. '소'가 있는 곳을 찾는 데에 평균적으로 O(N)의 시간 복잡도를 가지며, '소'를 '닭'으로 변경하는 동작 자체는 O(1)의 시간 복잡도를 갖습니다. O(N)의 시간 복잡도로 '소'의 데이터를 확인 및 변경할 수 있는 것입니다.
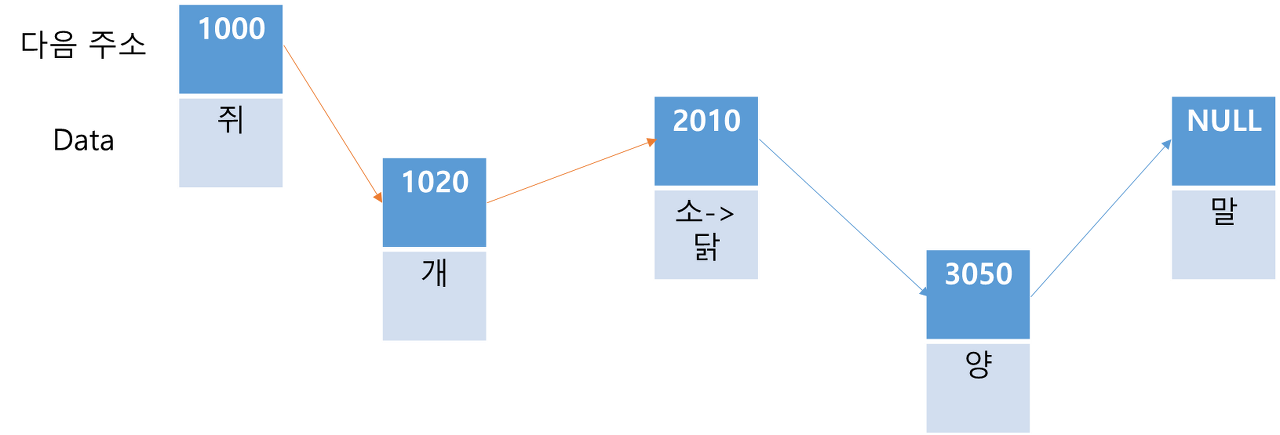
원소 삽입 및 삭제(LinkedList)
'양'과 '말' 사이에 '뱀'을 추가한다고 하면, '쥐'부터 해서 '양'을 찾아가야 하는데 O(N)의 시간 복잡도를 갖습니다. '양'이 가리킬 다음 주소에 어느 메모리에 새롭게 저장된 '뱀'의 주소를 저장하고, '뱀'은 다음 주소인 '말'을 가리킵니다(O(1)). 결과적으로 O(N)의 시간 복잡도를 갖습니다.(리스트의 크기 5 -> 6)
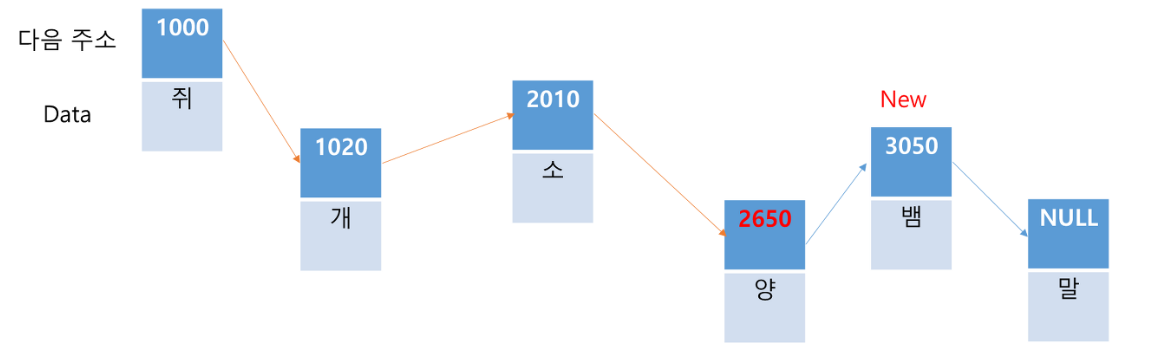
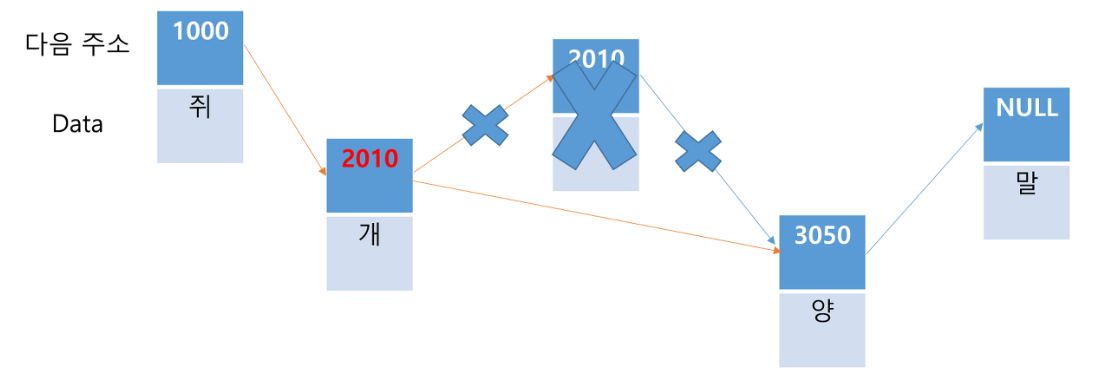
'소'를 삭제한다고 하면, '쥐'부터 해서 '소'를 찾아가야 하는데 O(N)의 시간 복잡도를 갖습니다. '소'를 삭제하면 '개'가 가리킬 다음 주소를 '양'의 주소로만 바꾸어주면 되기 때문에 이 동작은 O(1)이다. 결과적으로 O(N)의 시간 복잡도를 갖는다. (리스트의 크기 5 -> 4)
Array vs ArrayList vs LinkedList
| Array | ArrayList | LinkedList | |
|---|---|---|---|
| 선형 vs 비선형 | 선형 | 선형 | 선형 |
| 순차 vs 연결 | 순차 | 순차 | 연결 |
| 크기 | 고정 | 가변 | 가변 |
| 접근 | O(1) | O(1) | O(N) |
| 삭제, 추가 | O(N) | O(N) | O(N) |
- 크기가 가변적인 배열이 필요하다면 ArrayList
LinkedList의 삭제, 추가 시간 복잡도는 O(N)이지만 Array나 ArrayList보다 빠름 - 데이터의 삭제 추가가 많을 때 -> LinkedList
- 데이터의 접근이 많을 때 -> Array, ArrayList
- Array, ArrayList는 인덱스가 있지만 LinkedList는 없으므로 인덱스가 필요하면 Array, ArrayList 필요 없다면 LinkedList
객체 지향 5원칙
- 단일 책임 원칙 (Single Responsiblity Principle)
모든 클래스는 각각 하나의 책임만 가져야 한다. 클래스는 그 책임을 완전히 캡슐화해야 함을 말한다.
cf) 캡슐화: 하나의 캡슐(capsule)로 만들어 데이터를 외부로부터 보호하는 것을 말한다.
ex) 사칙연산 함수를 가지고 있는 계산 클래스가 있다고 치자. 이 상태의 계산 클래스는 오직 사칙연산 기능만을 책임진다. 이 클래스를 수정한다고 한다면 그 이유는 사직연산 함수와 관련된 문제일 뿐이다.
- 개방-폐쇄 원칙 (Open Closed Principle)
확장에는 열려있고 수정에는 닫혀있는. 기존의 코드를 변경하지 않으면서(Closed), 기능을 추가할 수 있도록(Open) 설계가 되어야 한다는 원칙을 말한다.
ex) 캐릭터를 하나 생성한다고 할때, 각각의 캐릭터가 움직임이 다를 경우 움직임의 패턴 구현을 하위 클래스에 맡긴다면 캐릭터 클래스의 수정은 필요가없고(Closed) 움직임의 패턴만 재정의 하면 된다.(Open)
- 리스코프 치환 원칙 (Liskov Substitution Principle)
자식 클래스는 언제나 자신의 부모 클래스를 대체할 수 있다는 원칙이다. 즉 부모 클래스가 들어갈 자리에 자식 클래스를 넣어도 계획대로 잘 작동해야 한다.
자식클래스는 부모 클래스의 책임을 무시하거나 재정의하지 않고 확장만 수행하도록 해야 LSP를 만족한다.
-
인터페이스 분리 원칙 (Interface Segregation Principle)
한 클래스는 자신이 사용하지않는 인터페이스는 구현하지 말아야 한다. 하나의 일반적인 인터페이스보다 여러개의 구체적인 인터페이스가 낫다. -
의존 역전 원칙 (Dependency Inversion Principle)
의존 관계를 맺을 때 변화하기 쉬운 것 또는 자주 변화하는 것보다는 변화하기 어려운 것, 거의 변화가 없는 것에 의존하라는 것이다. 한마디로 구체적인 클래스보다 인터페이스나 추상 클래스와 관계를 맺으라는 것이다.