DP(Dynamic Programming)

DP란?

DP는 다시 계산할 필요가 없도록 하위 문제의 결과를 저장하는 것입니다. 이 과정은 지수에서 다항식으로 시간 복잡도를 줄입니다.

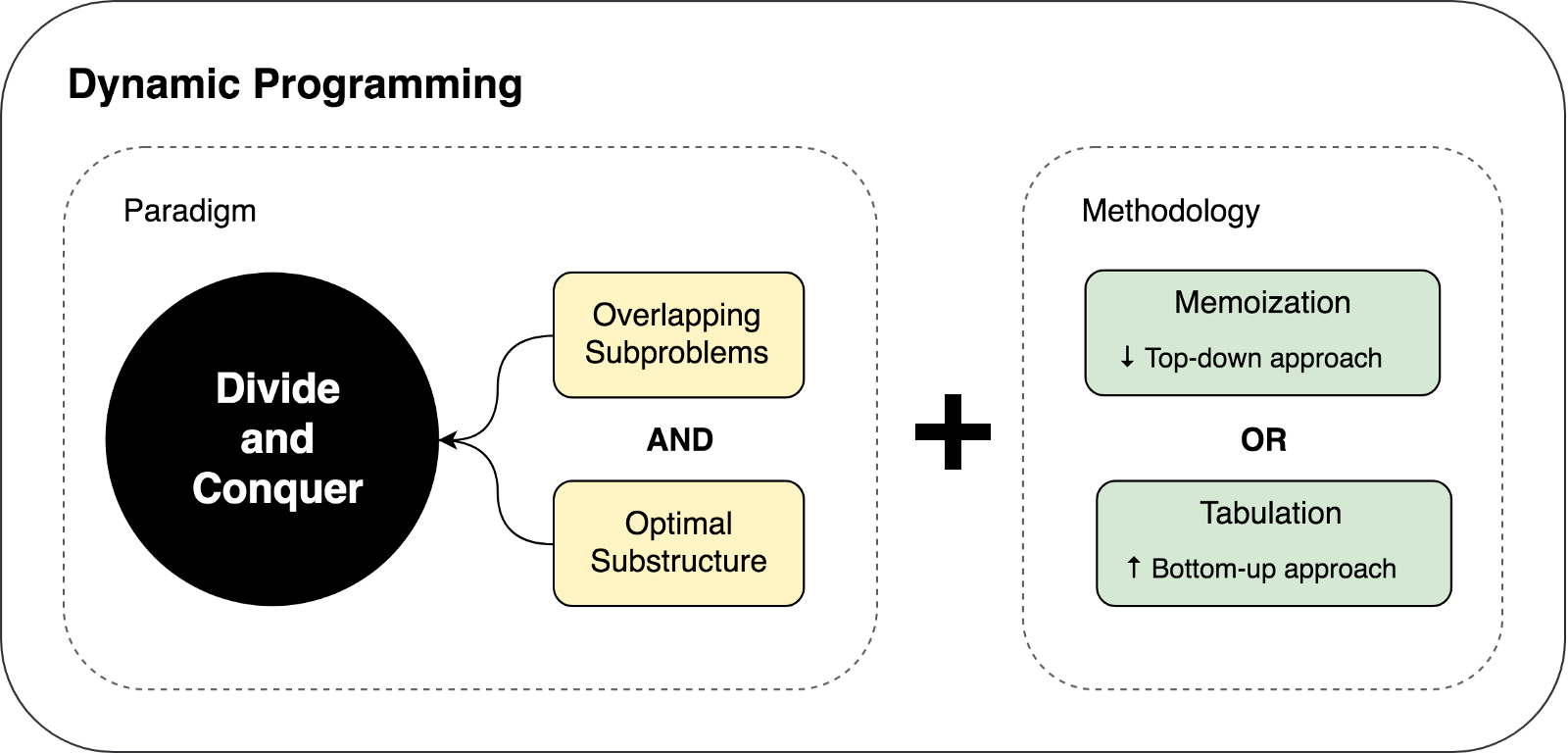
동적 계획법에는 분할 정복에 아래 개념이 추가됩니다.

• 반복되는 서브 문제(Overlapping Subproblems)
  문제를 해결하는 과정에서 동일한 하위 문제가 여러 번 해결되는 문제의 속성입니다.
• 최적 부분 구조(Optimal Substructure)
  문제에 대한 최적해는 작은 하위 문제에 대한 최적해를 결합하여 얻을 수 있습니다.
  cf) 병합정렬의 경우 부분으로 나누어 정렬하고 합칠 때 다시 대소 비교를 통해 정렬을 수행해야 합니다.

예시(fibonacci)

• 재귀(naive approach)

# Function to find nth fibonacci number
def fib(n):
    if (n <= 1):
        return n
    x = fib(n - 1)
    y = fib(n - 2)
  
    return x + y
  
n = 5;
  
# Function Call
print(fib(n))

Time Complexity: O(2^n)

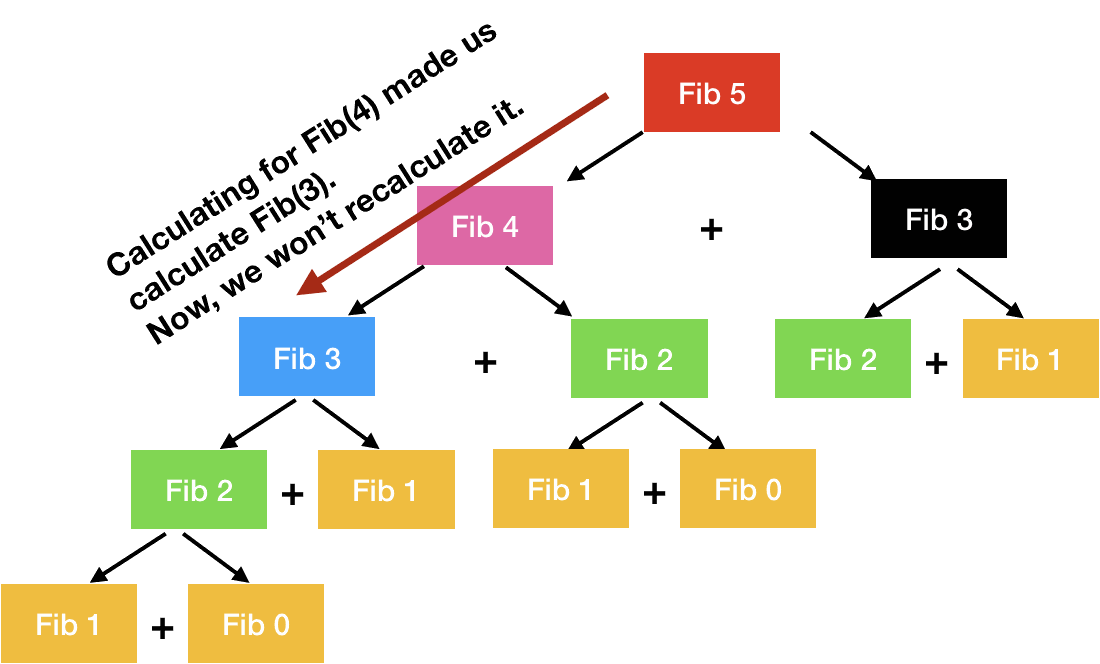
• Memoization(Top-down approach)
  메인 문제를 분할하면서 해결하는 방법입니다.
  

F = [-1]*50 #array to store fibonacci terms

def dynamic_fibonacci(n):
  if (F[n] < 0):
    if (n==0):
      F[n] = 0
    elif (n == 1):
      F[n] = 1
    else:
      F[n] = dynamic_fibonacci(n-1) + dynamic_fibonacci(n-2)
  return F[n]

if __name__ == '__main__':
  print(dynamic_fibonacci(46))

Time complexity: O(n)

• Tabulation(Bottom-up approach)
  가장 작은 문제를 먼저 해결하고 최종적으로 메인 문제를 해결하는 방법입니다.

F = [0]*50 #array to store fibonacci terms

def fibonacci_bottom_up(n):
  F[n] = 0
  F[1] = 1

  for i in range(2, n+1):
    F[i] = F[i-1] + F[i-2]
  return F[n]

if __name__ == '__main__':
  print(fibonacci_bottom_up(46))

Time complexity: O(n)

Memoization & Tabulation

Memoization은 문제를 해결하는 자연스러운 방법이기 때문에, 복잡한 문제를 다룰 때 코딩이 더 쉽습니다. 많은 조건들을 처리하면서 특정 순서를 고안하는 것은 Tabulation에서는 어려울 수 있습니다.

또한, 모든 하위 문제의 해결책을 찾을 필요가 없는 경우에는 Memoization을 사용하는 것이 좋습니다.

그러나 많은 재귀 호출이 필요한 경우, Memoization은 재귀 호출을 스택에 쌓아 더 깊은 재귀 호출의 해결책을 찾는 것으로 인해 메모리 문제가 발생할 수 있습니다. Tabulation에서는 이 문제를 신경쓰지 않아도 됩니다.