분할 정복

분할 정복이란?

한 문제를 둘 이상의 부분 문제(sub-problem)로 나누어 해결하고 이를 합쳐 원래 문제를 해결하는 기법입니다.

분할 정복 알고리즘은 다음과 같이 세 부분으로 나누어서 생각해 볼 수 있습니다.

분할 정복의 단계

① 분할: 동일한 타입의 하위 문제로 큰 문제를 분할합니다.
② 정복: 재귀적으로 하위 문제들을 해결합니다.
③ 병합: 적절히 해결된 결과를 사용해 큰 문제를 해결합니다.

재귀와 차이점

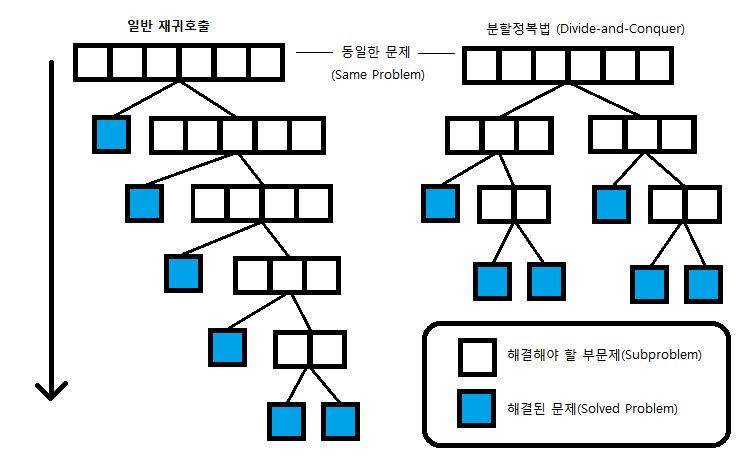
분할 정복이 일반적인 재귀 호출과 다른 점은 거의 같은 크기의 부분 문제로 나누는 것입니다. 재귀는 한 문제씩 푼다면, 분할 정복은 문제를 거의 같은 크기의 두 문제로 나누어서 해결합니다.

재귀를 이용한 수열의 합

int sum(int n)
{
	if(n == 1) 
		return 1;
	return sum(n - 1) + n;
}

분할 정복을 이용한 수열의 합

int sum(int n)
{
	if(n == 1) 
    	return 1;
	if(n % 2 == 1) 
    	return sum(n - 1) + n;
	return 2 * sum(n / 2) + (n / 2) * (n / 2);
}

분할 정복의 예 - 합병 정렬

① 분할: 전체 데이터를 반으로 지속적으로 분할합니다. 직접 문제가 해결되는 수준까지(데이터가 1개 남을 때까지) 분할합니다.
② 정복: 데이터가 1개가 남으면 그 자체로 이미 정렬된 상태입니다. 분할된 2개의 데이터를 정렬합니다.(하위 문제 해결)
③ 병합: 정렬된 하위 문제를 병합하여 전체 내역을 정렬합니다.

vector<int> sd; // 임시로 숫자를 저장하기 위한 벡터 sd 선언
// merge 쪼개진 벡터 합치기
void merge(vector<int>& li, int p, int k, int q)
{
	int left = p; // 맨 앞 인덱스
	int m = k + 1; // 가운데 인덱스
	int fin = p; // 최종 벡터에 저장하기 위한 인덱스
	// 작은 순서대로 벡터에 삽입
	while (left <= k && m <= q) { // left > k or m > q이면 while문 종료
		if (li[left] <= li[m]) // 2개의 벡터를 합칠 때 맨 앞 원소끼리 비교
		{
			sd[fin] = li[left]; // 벡터 sd에 작은 숫자 저장
			left++; // 다음 숫자를 가리키도록 +1
		}
		else {
			sd[fin] = li[m]; // 벡터 sd에 작은 숫자 저장
			m++; // 다음 숫자를 가리키도록 +1
		}
		fin++; // 다음 공간을 가리키도록 +1
	}
	// 나머지 데이터 저장
	if (left > k) // left>k가 성립하여 while문이 종료되었다면
	{
		while (m <= q) // m>q만족할 때까지 남은 데이터 저장
		{
			sd[fin] = li[m]; // 데이터 저장
			m++;
			fin++;
		}
	}
	else if (m > q) // m>q가 성립하여 while문이 종료되었다면
	{
		while (left <= k) // left>k 만족할 때까지 남은 데이터 저장
		{
			sd[fin] = li[left]; //데이터 저장
			left++;
			fin++;
		}
	}
	// 데이터 복사
	for (int i = p; i <= q; i++)
		li[i] = sd[i]; // li 벡터에 임시 벡터 sd의 원소 그대로 넣기
}
void merge_sort(vector<int>& li, int p, int q)
{
	if (p < q) {
		int k = (p + q) / 2;
		merge_sort(li, p, k);
		merge_sort(li, k + 1, q);
		merge(li, p, k, q);
	}
}