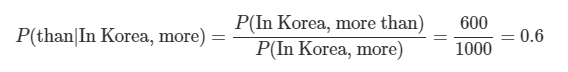N-gram 언어모델
- 자연어를 통계적으로 잘 처리해주는 전통적인 방식
- 이전에 등장한 모든 단어를 고려X / n개로 정한 일부 단어에만 접근
👓 n-gram 언어모델의 발달과정
자연어 - 우리가 일상에서 사용하는 언어
자연어 처리 - 자연어 의미를 분석해서 컴퓨터가 처리할 수 있도록
언어 모델 - 자연어 처리를 위한 방법
기계에게 많은 코퍼스를 훈련시켜서 언어 모델을 통해 현실에서의 확률 분포를 근사하는 것이 언어 모델의 목표이다.
(문장이 입력되어 -> 문장에 대한 확률(문장이 얼마나 '그럴듯'한지)을 계산)
- 언어모델로 할 수 있는거
a) 여러가지 문장이 주어졌을 때 가장 그럴듯한 문장을 만들수 있음
b) 문장의 앞부분이 주어졌을 때 다음 단어를 예측할 수 있음
자연어를 처리하기 위해서 이 언어 모델을 만들어서 사용한다.
자연스러운 단어 시퀀스를 찾아내기 위해서는 비지도 학습(말뭉치 내에 있는 수많은 단어 중 가장 적절한 결합을 찾아내는 작업)을 사용해야한다. 이는 현실적으로 한계가 있어 지도학습으로 바꾸어 처리한다.
Bag of Words는 한 문서 내에 단어들이 얼마나 등장했는지 빈도수를 측정하여 텍스트 데이터를 수치화하는 방법이다. 단어들 간의 짜임이나 유사성은 보지않고 쪼개진 토큰들의 set만 본다.
하지만, 이 방법은
1) 단어의 순서를 알 수 없고
2) 문장 내 단어가 많아질수록 전체 계산량이 높아지고 메모리 사용이 많아지는 희소문제가 발생한다.
희소 문제 : 충분한 데이터를 관측하지 못하여 언어를 정확히 모델링 하지 못하는 문제
(I love you라는 문장 시퀀스가 실제로 존재하는데 코퍼스에 단어 시퀀스가 없다고 해서 이 확률을 0 또는 정의되지 않는 확률이라고 하는 것)이다.
3) 가장 많은 빈도로 출현한 단어들의 힘이 강해진다.
(TF-IDF로는 多빈도의 단어에 힘이 과하게 실어진다는 문제점을 해결할 수는 있지만, 단어들간의 유사성을 판단하기엔 무리가 있다.)
이 한계를 해결하기위해 자기회귀 언어모델을 사용한다.
자기회귀 언어모델이란 자기 자신의 입력을 예측하는 통계 기반의 언어 모델(SLM)이다. 이 모델을 사용하면 다음에 올 토큰의 분포를 이전의 모든 토큰들의 조건부 확률로 표현한다.
input-이전에 나온 토큰 / output-다음에 나올 토큰
하지만 이 역시 여전히 희소문제를 가지고있다.
==> 희소성 등 여러 한계점을 보완하기 위해 통계적 분석 방법 언어 모델인 N-gram을 사용한다.
🧵 기본 개념
BoW와 TF-IDF처럼 빈도수를 측정하여 벡터로 표현.
n개의 단어 시퀀스만을 분석 대상으로 삼음
N = 1,2,3 -> Uni-gram, Bi-gram, Tri-gram
N = 4, 5 -> 4-gram, 5-gram
- N-1개의 단어에만 의존한다.
EX) 4-gram일 경우..

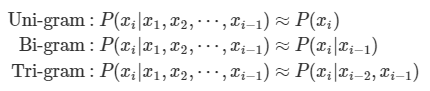
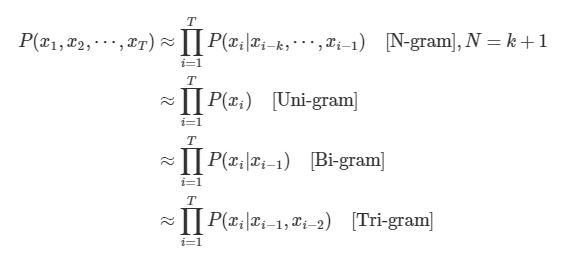

🎯 자기회귀 모델 VS N-gram
자기회귀 모델 - 코퍼스에 찾고자하는 모든 단어 시퀀스가 존재해야 한다.
ex) "In Korea, more than half of residents" 문장 자체가 존재해야한다.
n-gram - 일부 시퀀스만 존재해도 확률 계산 가능
ex) "of residents" 시퀀스만 존재해도 "In Korea, more than half of residents" 계산 가능
🧨 N-gram의 한계
1) 희소 문제
희소문제를 약간 완화하기는 하지만, 학습 데이터인 코퍼스가 무한하지 않기 때문에 필요한 시퀀스의 확률이 0이 될 가능성이 아직 존재한다.
-> : 학습한 코퍼스 안에 단어 시퀀스가 없다면 확률이 0 또는 정의되지 않아 정확하게 단어를 예측하지 못한다.
(= 원-핫 임베딩과 유사(문법적 관계, 의미적 관계 학습 X) --> 워드 임베딩으로 해소)
2) 장기 의존성 문제
순서만을 고려하다 보니, 문장 앞쪽의 문맥을 고려하지 않음
-> 잘못된 문장을 만들게 될 수도 있다. (긴 문장일수록 더!)
ex) “한국의 수도는 서울이다.” "한국의 수도는 파리이다."
"서울이다."가 답인데 "파리이다."라는 데이터 셋이 더 많으면 후자의 문장을 만들게 된다.
N을 늘리게 되면 해소되지 않을까?
- N을 크게 선택
1) 희소 문제 부활
(실제로 N>=7 에서 시퀀스 등장 확률이 0에 수렴함)
2) 모델 사이즈 커짐(코퍼스 모두에 대해서 카운트해야하기 때문)
- N을 작게 선택
희소성 문제(0될 문제)는 줄어들지만, 단어 예측의 정확도는 낮아진다.
3) 학습하지 못한 문장에 대하여
학습되지 않은 자료는 예측하지 못한다 = 일반화 능력의 결여
(유사성을 고려하지 못하기 때문. n-gram의 단어들은 모두 독립변수로 본다.)
🎪 N-gram 한계에 대한 해결책
1) 스무싱(Smoothing)
- 희소 문제 해결
- 모든 단어 시퀀스의 출현빈도에 작은 값을 더해줘서 확률이 0이 되지 않게 한다.
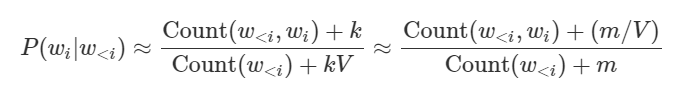
2) 백오프(Backoff)
- 희소 문제 해결
- 특정 단어가 다음에 올 확률(분자)이 0인 경우에만! N을 줄여 희소성 문제 해결
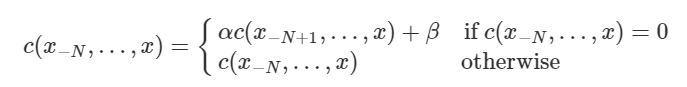
3) Kneser-Ney 스무싱(KN smoothing)
- 앞의 단어의 다양성을 체크하여 뒤 단어를 예측
- 반복된 단어와 동일한 품사가 나왔을때 확률높아지고 어쩌고
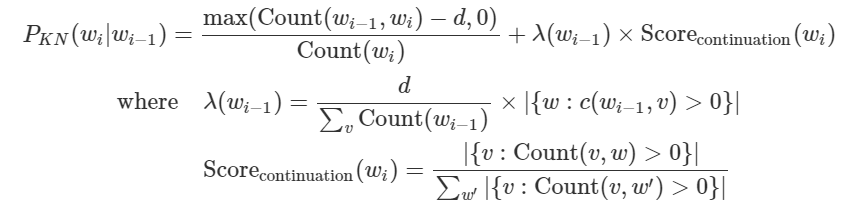
🎬 전반적인 흐름 이해하기
https://www.youtube.com/watch?v=hM49MPmakNI
언어 모델의 가장 큰 목표는
문장에 대한 확률을 할당하자
이다.
연쇄법칙을 사용해서 조건부 확률의 곱으로 나타낸다.



its water is so transparent that the
란 문장에서 the가 나올 확률을 구한다면

요러케
근데 계산은 어렵다.
분모(가능한 문장)는 너무 많고, 분자(특정문장)은 너무나도 작기 때문에
-> Markov Assumption(마르코프 가정) 이용해 확률 계산
: 특정 시점에서 어떤 상태의 확률은 최근 상태에만 의존한다는 가정
즉, 조건부확률은 문장 단위로 다루기 어렵기 때문에 이전의 '한 단어' 혹은 '두 단어'만을 다루기로 한다.
-> N-gram
: 이전 k개의 단어만 고려하기.
문장이 길어질수록 연산량이 기하급수적으로 증가.
크기가 큰 N 필요!!!!
그 남자는 공을 차서 학교 유리창을 깼기 때문에, 학교 선생님은 ( )를 불러서 혼냈다.
()를 알려면 적어도 10개 가량의 이전 단어를 봐야한다. -> 경우의 수가 너무 많아짐!
-> 장기 정보를 다루기 위해서는 n-gram보다 좋은 모델 필요