세미나를 준비하며.. 전반적인 흐름을 공부해봤다.
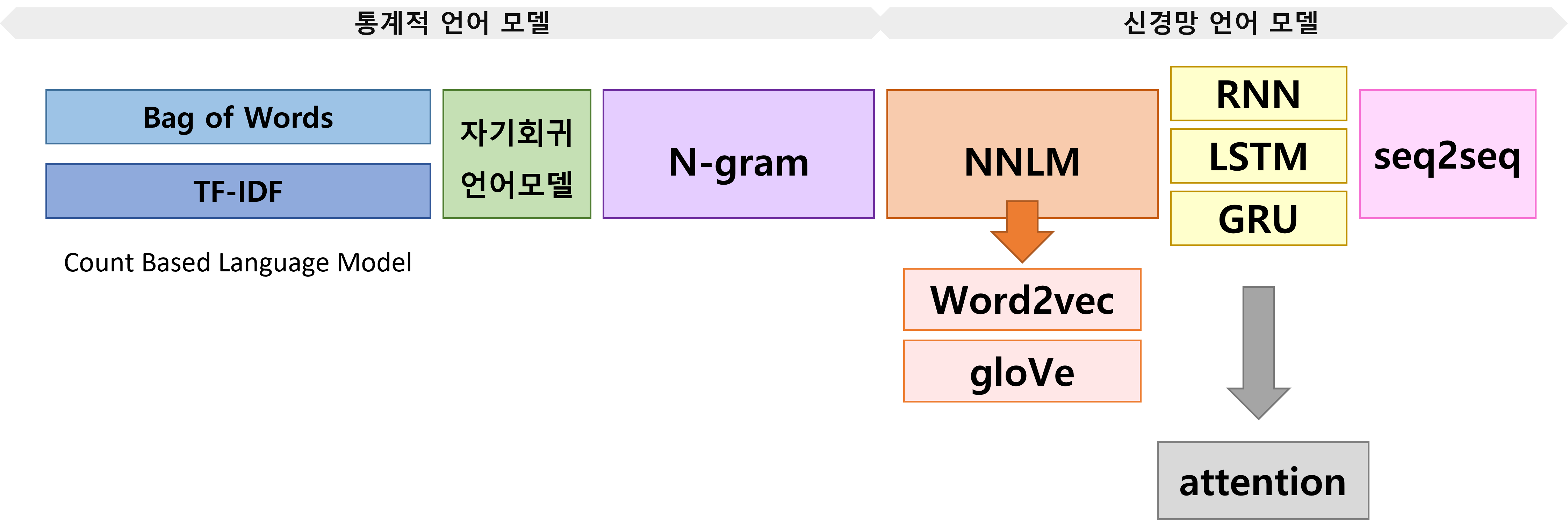
🍔 전체 흐름도
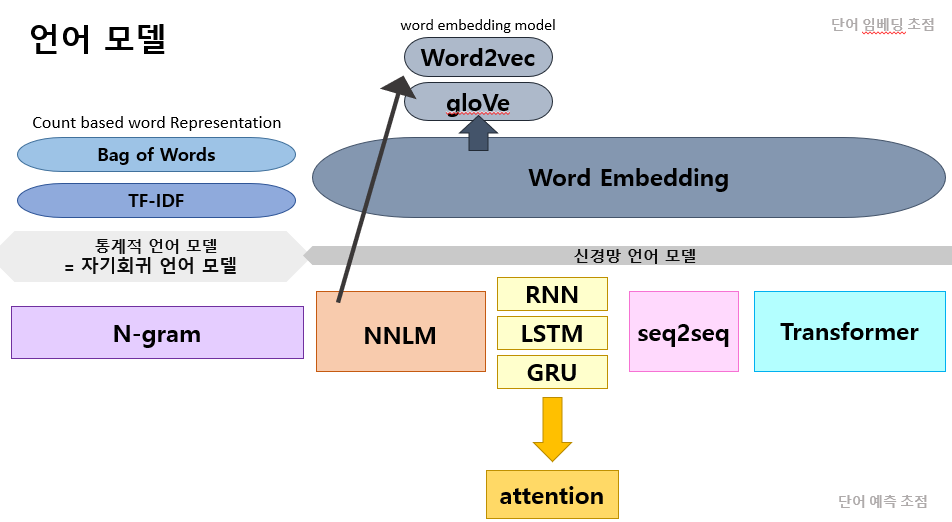
0) 단어 임베딩
0-1) 카운트 기반의 단어 표현
- 모델은 아님(벡터 표현 중 하나)
🏀 Bag of Words
단어에 정수 인덱스 부여 -> 인덱스 위치에 단어 토큰의 등장 횟수를 기록한 벡터 만듦
(단어의 빈도수(정수))
⚽ DTM
BoW를 기반하여 행렬화
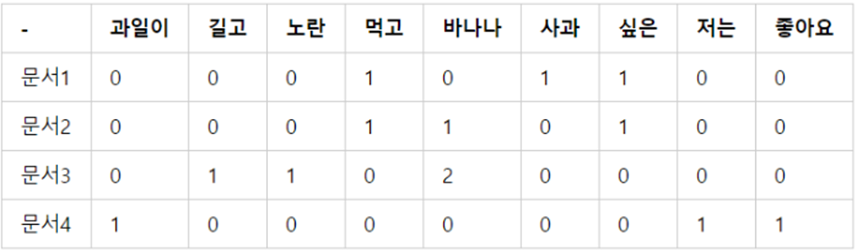
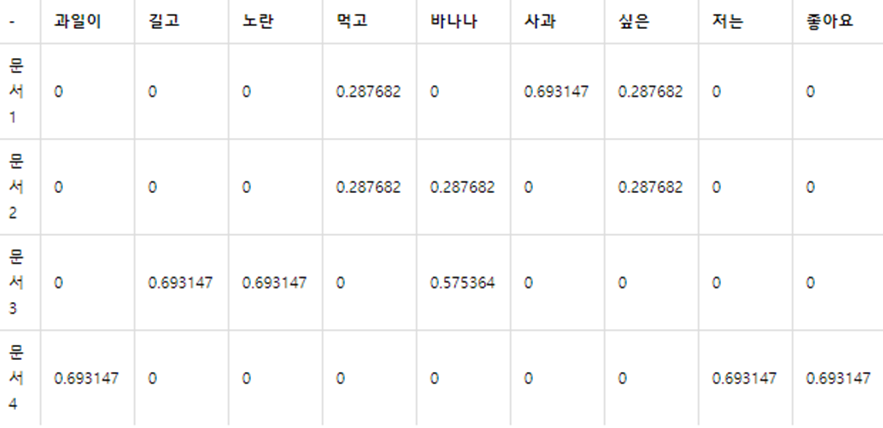
🥎 TF-IDF
: DTM에서 각 단어의 중요도를 가중치로 부여
- 해당 문서에 해당 단어가 많이 등장하는 것이라면 중요한 것이지만, 애초에 모든 문서에서 많이 등장하는 단어(동사 등)였다면 그만큼 감점을 시키자
TF : 1개 문서에 특정 단어 등장 빈도(단어의 빈도수)(= DTM)
DF : 특정 단어가 나타나는 문서의 개수
IDF : 가중치를 낮추기 위해 DF를 역수 취한 것
ex) 100개의 문서 중 apple이 2개의 문서에서 등장 --- DF==2
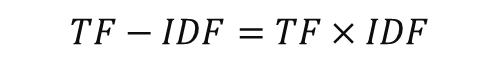
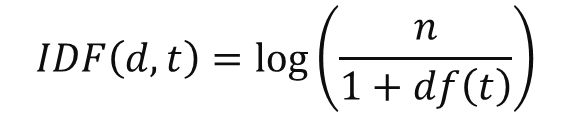
0-2) 워드 임베딩
카운트 기반의 단어표현은 단어의 빈도수를 세는 것에 국한하기때문에 단어들 사이의 유사성 등을 알 수 없다는 한계가 있음.
이에 얕은 신경망을 이용해 단어들을 학습시키면서 임베딩 하는 '워드 임베딩'이 제기됨.
대표적으로 word2vec과 glove 등이 있다.
1) 언어 모델
: (자연어를 컴퓨터가 처리하도록 하기 위해서) 문장 혹은 단어에 확률을 할당하여 컴퓨터가 처리할 수 있도록 하는 모델
-> 문장이 얼마나 그럴듯한지 계산
🧂 기능
a) 여러가지 문장이 주어졌을 때 가장 그럴듯한 문장을 만들 수 있음
b) 문장의 앞부분이 주어졌을 때 다음 단어를 예측할 수 있음
2) 통계적 언어 모델(SLM)
공통적인 문제) 희소 문제(sparsity problem) 발생
희소문제
: 학습한 코퍼스 안에 단어 시퀀스가 없다면
확률이 0 또는 정의되지 않아 정확하게 단어를 예측하지 못하는 문제
≒ 자기회귀 언어 모델(ALM)
: 자기 자신의 입력을 예측하는 통계 기반의 언어 모델
-
현재에 와서 '통계적 언어모델'이란 단어대신 불리는 이름
-
거의 모든 언어모델이 자기회귀 모델이다(transformer, gpt)
하지만, 모든 언어모델이 자기회귀인 것은 아니다(BERT)
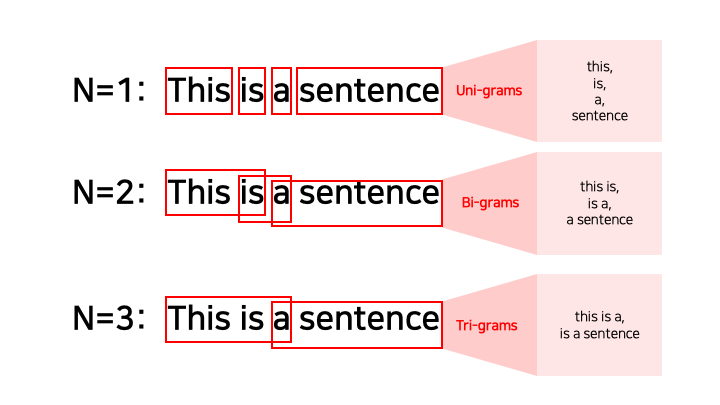
2-1) N-gram
: n개의 단어 시퀀스만을 분석 대상으로 빈도수를 측정하여 벡터로 표현하는 통계적 언어모델
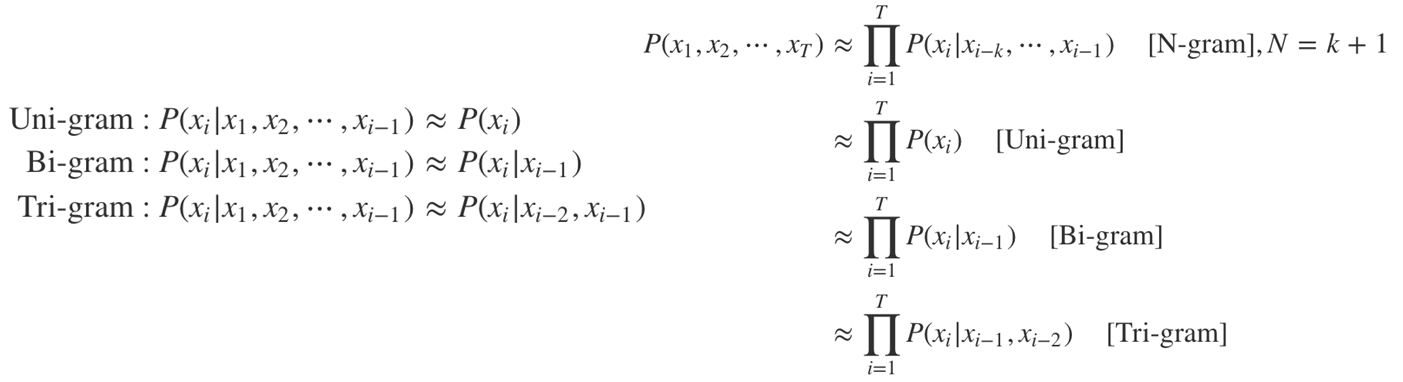
마르코프 가정(Markov assumption) 이용
특정 시점에서 어떤 상태의 확률은 최근 상태에만 의존한다는 가정이다. xi의 확률을 그 이전에 있는 토큰 전부가 아닌 일부 토큰으로부터 추론할 수 있다는 것이다.
> 자기회귀 언어 모델 vs N-gram
N-gram의 한계
1) 희소 문제 : 확률이 0이 될 가능성 존재
2) 장기 의존성 문제 : 문장 앞쪽의 문맥을 전혀 고려하지 않음(문장이 길어질수록 정확성 떨어질 가능성
3) 고차원 벡터의 사용문제
이에 신경망을 사용한 언어모델로 발전하게 된다.
