[Research] Quantization

bluein·2024년 6월 7일
Research
1

2. Quantization

모델의 파라미터를 낮은 비트 수로 표현하여 모델 크기와 계산량을 줄이는 방법

1) Static Quantization

학습 후 모델의 weight와 activation을 양자화하는 방법

  • 개요: 모델이 학습을 마친 후, 32-bit 부동 소수점으로 표현된 weight와 activation을 8-bit 정수로 변환하여 저장하는 방법

  • 과정:

    • 학습이 완료된 모델을 대상으로 진행
    • 모델의 weight와 activation 값을 통계적으로 분석하여 최적의 quantization 범위를 설정
    • 설정된 범위에 따라 32-bit 값을 8-bit 정수로 변환

  • 장점:

    • 메모리 사용량 대폭 감소
    • 연산 속도 향상
    • 모델 배포 시 필요한 저장 공간 절약

  • 단점:

    • Quantization 과정에서 일부 정보 손실이 발생할 수 있어 모델 성능이 다소 저하될 가능성.

  • 관련 연구:

    • "Quantizing deep convolutional networks for efficient inference: A whitepaper" by Y. LeCun, L. Bottou, et al. (2016)

      • 이 논문에선, weight의 채널별 양자화(per-channel quantization)와 activation의 레이어별 양자화(per-layer quantization)를 사용하여 8비트 정밀도로 변환

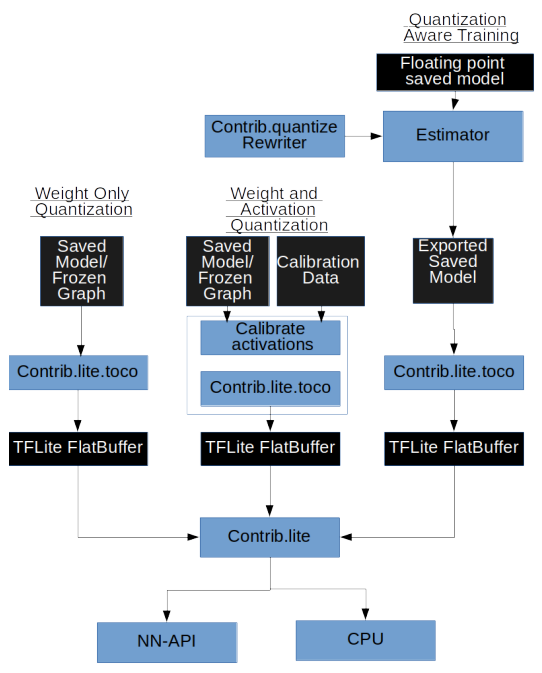
      • 다양한 CNN 아키텍처에서 부동 소수점 네트워크와 비교할 때 분류 정확도가 2% 이내로 유지될 수 있음

      • 학습 후 weight와 activation을 8비트 정밀도로 변환

      • Per-channel quantization

        Qi(xi)=round(xi/Δi)⋅ΔiQ_i(x_i) = \text{round}(x_i / \Delta_i) \cdot \Delta_i

      • xix_i는 채널 ii의 값, Δi\Delta_i는 채널 ii의 scale factor

      • Per-layer quantization

        Qlayer(x)=round(x/Δlayer)⋅ΔlayerQ_{\text{layer}}(x) = \text{round}(x / \Delta_{\text{layer}}) \cdot \Delta_{\text{layer}}

      • Δlayer\Delta_{\text{layer}}는 해당 레이어의 scale factor

      • 이를 통해 모델 크기를 4배 줄이고, CPU 및 DSP에서 2-3배, 고정 소수점 SIMD 기능이 있는 특수 프로세서에서는 최대 10배의 속도 향상을 얻을 수 있음

2) Dynamic Quantization

추론 시 weight를 양자화하는 방법

  • 개요: 모델의 추론 과정에서 weight를 실시간으로 8-bit 정수로 변환하여 연산을 수행하는 방법

  • 과정:

    • 모델이 추론을 시작할 때 weight를 동적으로 8-bit 정수로 변환
    • 변환된 weight를 사용하여 연산을 수행
    • Activation 값은 32-bit 부동 소수점으로 유지

  • 장점:

    • Quantization에 필요한 준비 과정이 간단
    • 추론 시 연산 효율성 증대
    • 메모리와 계산 자원 절약

  • 단점:

    • Static Quantization에 비해 성능 최적화 수준이 낮을 수 있음
    • 실행 시 추가적인 변환 연산 필요

  • 관련 연구:

    • "Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference" by J. Jacob, P. Warden, et al. (CVPR 2018)

      • 이 논문에서는, 모바일 디바이스와 같은 저전력 장치에서의 딥러닝 모델의 효율적이고 정확한 추론을 위해, 정수 산술(Integer-Arithmetic)만을 사용하는 양자화 방식을 제안

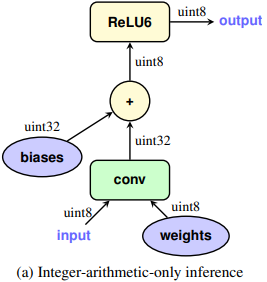
    • 모델의 weight와 activation 값을 8비트 정수로 양자화
    • 이로 인해 연산의 복잡도가 감소하고, 추론 속도가 향상
    • 양자화된 값은 실수 값을 정수로 변환한 후, scale factor를 사용하여 정확도를 보정
    • 이는 다음과 같은 수식을 통해 표현

      x^=Sx(x−Zx)\hat{x} = S_x (x - Z_x)

    • x^\hat{x}는 양자화된 값, SxS_x는 scale factor, ZxZ_x는 zero point

      Zero point란 ?
      실제 값의 양자화된 표현이 0이 되는 값
      이를 통해 실제 값의 범위를 양자화된 값으로 적절하게 매핑할 수 있음

    • 양자화된 행렬 곱셈은 다음과 같이 정의

      Y^=SwSx∑k(W^i,k−Zw)(X^k,j−Zx)+Zy\hat{Y} = S_w S_x \sum_{k} (\hat{W}_{i,k} - Z_w)(\hat{X}_{k,j} - Z_x) + Z_y

    • W^\hat{W}와 X^\hat{X}는 양자화된 weight와 입력값,
      SwS_w와 SxS_x는 각각의 scale factor,
      ZwZ_w, ZxZ_x, ZyZ_y는 zero point
    • 이 수식은 양자화된 weight와 입력 값을 scale factor로 조정하여 정수 연산을 통해 행렬 곱을 수행한 후, zero point를 적용하여 최종 출력을 얻는 과정
    • 이를 통해 부동 소수점 연산 대신 정수 연산을 사용하여 계산 효율성을 높일 수 있음

3) Quantization Aware Training

학습 시 양자화를 고려하여 학습하는 방법

  • 개요: 모델이 학습 과정에서 quantization의 영향을 고려하도록 하여 quantization로 인한 성능 저하를 최소화하는 방법

  • 과정:

    • 학습 과정에서 weight와 activation 값을 quantization 시뮬레이션
    • 모델이 quantization된 값으로 연산을 수행하도록 학습
    • 학습 완료 후 실제 quantization을 적용할 때의 성능 저하를 줄이기 위해 미리 조정된 모델 생성

  • 장점:

    • Quantization로 인한 성능 저하 최소화
    • 모델이 quantization 환경에 적응하도록 학습되므로 더 높은 정확도 유지

  • 단점:

    • 학습 과정이 더 복잡하고 오래 걸릴 수 있음
    • 추가적인 계산 자원 필요

  • 관련 연구:

    • "Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference" by J. Jacob, P. Warden, et al. (2018)

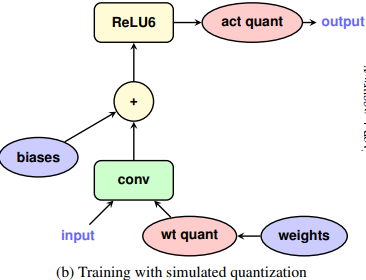
      • 양자화된 모델의 정확도를 유지하기 위해 학습 과정에서 "Fake Quantization" 사용

        Fake Quantization 이란?

        • 학습 중에 모델이 실제로 양자화된 상태에서 동작하는 것처럼 시뮬레이션하는 기법
        • 모델이 학습하는 동안 weight와 activation 값을 8비트 정수로 변환하여 양자화된 값으로 계산
        • 모델이 양자화로 인한 오류를 학습하면서 보정
        • 이는, 학습 후 실제 양자화를 적용했을 때 모델의 정확도가 크게 떨어지지 않도록 함

      • 학습 중에 정수 양자화를 시뮬레이션하여 양자화 오류를 모델이 학습하도록 함

      • 양자화로 인한 오류를 최소화하여 양자화 후에도 모델의 정확도를 크게 저하시키지 않음

4) Post-Training Quantization

학습 후 모델의 weight를 양자화하는 방법

  • Static Quantization과 Post-Training Quantization은 개념적으로 유사하지만,
    Static Quantization은 주로 모든 레이어와 activation 값을 대상으로 하는 반면,
    Post-Training Quantization은 특정 최적화 기법이나 부분적인 양자화를 포함할 수 있음
  • 따라서 Post-Training Quantization은 더 유연하고 다양한 방법을 포함할 수 있는 반면, Static Quantization은 보다 일반적인 접근 방식

  • 개요: 학습된 모델의 weight를 8-bit 또는 4-bit 정수로 변환하여 메모리와 계산 자원을 절약하는 방법

  • 과정:

    • 학습이 완료된 모델의 weight를 양자화
    • Activation 값도 필요 시 양자화

  • 장점:

    • 기존 학습된 모델을 그대로 활용할 수 있음
    • 메모리 사용량과 연산 자원 절약

  • 단점:

    • 양자화 과정에서 일부 성능 저하 가능

  • 관련 연구:

    • "Post-Training 4-bit Quantization of Convolutional Networks for Rapid-Deployment" by A. Mishra, E. Nurvitadhi, et al. (2017)

      • 위 논문은 전체 데이터셋이나 fine-tuning 없이 정확도를 유지할 수 있는 4-bit post training quantization 방법을 제안
      • 아래와 같은 세 가지 Contribution을 제안하고 있음

        • i) Analytical Clipping for Integer Quantization (ACIQ)

          • Tensor 값의 범위를 제한하여 quantization noise를 최소화
          • 다음과 같은 clipping 값 α\alpha 최적화 수식 제안

          E((X−Q(X))2)=∫−ααf(x)⋅(x−α)2dx+∑i=02M−1∫−α+iΔ−α+(i+1)Δf(x)⋅(x−qi)2dx+∫α∞f(x)⋅(x−α)2dxE((X-Q(X))^2) = \int_{-\alpha}^{\alpha} f(x) \cdot (x-\alpha)^2 dx + \sum_{i=0}^{2^M-1} \int_{-\alpha + i\Delta}^{-\alpha + (i+1)\Delta} f(x) \cdot (x-q_i)^2 dx + \int_{\alpha}^{\infty} f(x) \cdot (x-\alpha)^2 dx

          • E((X−Q(X))2)E((X-Q(X))^2): Quantization 후 원본 값과 quantized 값 간의 MSE를 의미
          • ∫−αα\int_{-\alpha}^{\alpha}: Clipping 구간 내의 오차를 계산
          • ∑i=02M−1∫−α+iΔ−α+(i+1)Δ\sum_{i=0}^{2^M-1} \int_{-\alpha + i\Delta}^{-\alpha + (i+1)\Delta}: 각 quantization 구간 내의 오차를 계산
          • ∫α∞\int_{\alpha}^{\infty}: Clipping 구간 밖의 오차를 계산

        • ii) Per-channel bit allocation

          • 각 channel에 대해 최적의 비트 수를 할당

        • iii) Bias-correction

          • Quantization 후 값의 bias를 관찰하고 이를 보정하는 방법 제안

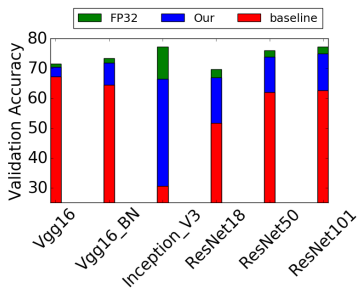
      • 위 그림과 같이, 제안된 방법이 정확도 손실을 최소화하고, retraining 없이도 높은 정확도를 유지할 수 있음

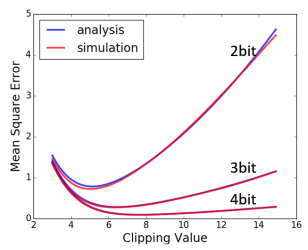
      • 위 그림은 다양한 Quantization level(2비트, 3비트, 4비트)에 대한 clipping 값의 함수로서의 예상 MSE
      • 분석 결과와 시뮬레이션 결과가 잘 일치함을 보여줌

5) Mixed-Precision Quantization

다양한 비트 수를 사용하여 양자화하는 방법

  • 개요: 모델의 각 층 또는 각 파라미터에 대해 적절한 비트 수를 선택하여 양자화하는 방법

  • 과정:

    • 모델의 특정 부분에 대해 최적의 비트 수를 선택
    • 중요한 층에는 높은 비트 수, 덜 중요한 층에는 낮은 비트 수를 적용

  • 장점:

    • 성능 저하를 최소화하면서 메모리와 계산 자원을 절약
    • 유연한 양자화 가능

  • 단점:

    • 복잡한 최적화 과정 필요

  • 관련 연구:

    • "HAQ: Hardware-Aware Automated Quantization with Mixed Precision" by Y. Wang, Y. Chen, et al. (2019)

      • 이 논문에선 새로운 DNN 하드웨어 가속기가 증가된 정밀도 (1-8 비트)를 지원하기 시작하며, 각 레이어의 최적 비트폭을 찾는 것이 필요하다고 주장
      • 기존의 양자화 알고리즘은 하드웨어 아키텍처를 무시하고 모든 레이어를 동일한 방식으로 양자화
      • 이 논문에서는 강화 학습을 활용한 Hardware-Aware Automated Quantization (HAQ) 프레임워크를 제안
      • RL 에이전트가 하드웨어 가속기의 피드백을 활용하여 양자화 정책을 자동으로 결정
      • RL 에이전트는 레이어별로 최적의 비트폭을 학습하고, 하드웨어 시뮬레이터로부터 직접 피드백을 수집

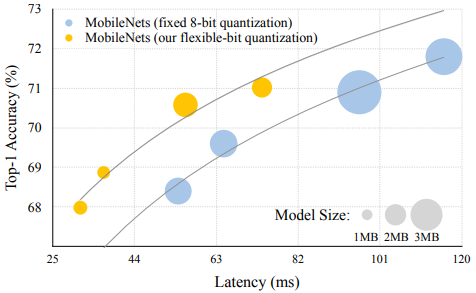
      • 위 그림은 MobileNets의 고정 8비트 양자화와 유연한 비트 양자화의 비교 (유연한 비트 양자화가 더 좋은 성능을 보임)

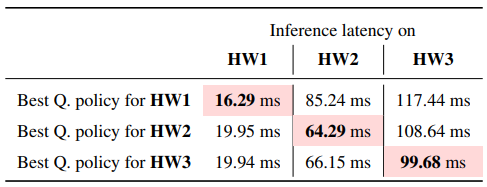
      • 위 테이블은 MobileNet-V1의 세 가지 하드웨어에서의 추론 latency 비교 (하드웨어별로 최적의 양자화 정책이 다름을 보여줌)

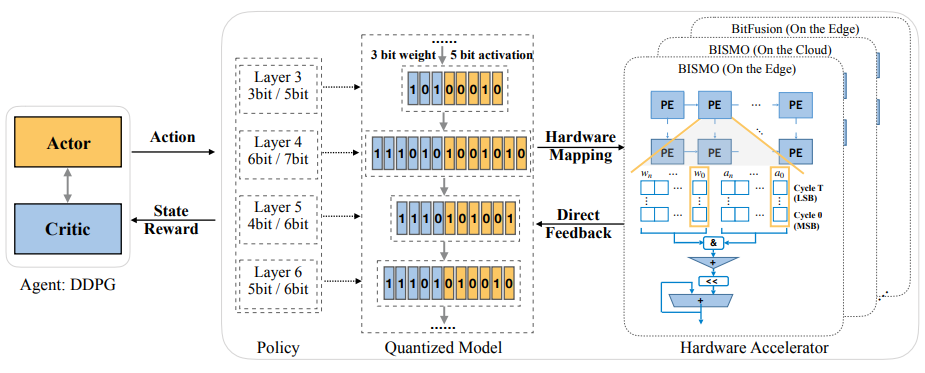
      • 위 그림은 HAQ 프레임워크 개요 (Actor-Critic 모델을 사용하여 양자화 정책을 학습)

6) Binarized Neural Networks

Weight와 activation을 1-bit로 표현하는 방법

  • 개요: 모델의 weight와 activation을 1-bit로 변환하여 연산 효율성을 극대화하는 방법
  • 과정:
    • 모델의 weight와 activation을 이진화
    • 이진 연산을 통해 모델 추론 수행
  • 장점:
    • 메모리 사용량과 연산 속도 극대화
  • 단점:
    • 성능 저하가 심할 수 있음
  • 관련 연구:
    • "Binarized Neural Networks" by M. Courbariaux, Y. Bengio, et al. (2016)
profile
bluein
AI Research Engineer
이전 포스트

[Research] Model Pruning

다음 포스트

[Research] Knowledge Distillation

0개의 댓글

관련 채용 정보