[Research] Knowledge Distillation

Knowledge Distillation

• 큰 모델(teacher model)에서 작은 모델(student model)로 지식을 전달
• 작은 모델이 큰 모델의 성능을 최대한 유지하도록 학습시키는 기법
• 주로 모델 compression과 효율적인 배포를 위해 사용
• 작은 모델의 정확도를 높이고, 큰 모델의 성능을 유지하면서도 경량화된 모델을 제공

---

주요 개념

• Teacher Model: 크고 복잡한 모델로, 높은 성능을 가지지만 리소스 요구가 큼
• Student Model: 작고 간단한 모델로, 낮은 리소스에서 작동 가능하게 설계됨
• Soft Targets
  • Teacher Model이 예측한 각 클래스에 대한 확률 분포 -> 정답 레이블 보다 더 많은 정보를 포함
  • 이를 통해 Student model은 각 클래스 간의 관계와 중요도를 더 잘 학습할 수 있음
  • Soft Target은 일반적으로 온도(T)를 사용하여 부드럽게 만들어짐
• Temperature Scaling
  • Soft Targets를 계산할 때 사용되는 기법
  • 확률 분포를 부드럽게 하여 더 많은 정보를 포함하게 함
  • Temperature(T)가 높을수록 예측 확률 분포가 부드러워지고, T가 낮을수록 예측 확률 분포가 더 뾰족해짐
  • 일반적으로 T는 1보다 큰 값을 사용

---

주요 단계

1. Teacher Model 학습: Teacher Model을 큰 데이터셋으로 학습하여 높은 성능을 얻음
2. Soft Targets 생성: Teacher Model이 예측한 확률 분포(Soft Targets)를 사용
3. Student Model 학습: Student Model을 Teacher Model의 Soft Targets와 함께 학습하여 성능 향상

---

주요 논문

---

1. Hinton et al., 2015

• Title: "Distilling the Knowledge in a Neural Network"
• Summary
  • Teacher 모델의 'Soft Target' 출력을 사용하여 작은 Student 모델을 학습시키는 Knowledge Distillation 방법을 제안
  • Teacher 모델이 예측한 Softmax 출력 분포를 학습 데이터로 활용하여 Student 모델이 Teacher 모델의 지식을 효과적으로 습득하도록 함
• Loss Function
  • Teacher의 Soft Target: $\mathbf{P_T} = softmax(\mathbf{a_T} / T)$
  • Student의 Soft Target: $\mathbf{P_S} = softmax(\mathbf{a_S} / T)$
  • Loss Function 구성:
    $L_{KD}(\mathbf{W_S}) = (1 - \alpha) \mathcal{H}(y_{true}, \mathbf{P_S}) + \alpha T^2 \mathcal{H}(\mathbf{P_T}, \mathbf{P_S})$
  • 여기서:
    • $y_{true}$는 실제 레이블이고, $\mathcal{H}$는 Cross-Entropy Loss를 의미하며, $\mathbf{P_T}$와 $\mathbf{P_S}$는 각각 Teacher와 Student 모델의 Softmax 출력
    • $T$는 Temperature 파라미터로, Softmax 출력을 부드럽게 하여 Teacher와 Student 모델 간의 분포 차이를 줄이는 역할을 함
    • $\alpha$는 Hard Target Loss와 Soft Target Loss 간의 가중치를 조절하는 하이퍼파라미터
  • 실제 레이블과 Student 모델의 예측 간의 Cross-Entropy Loss와 Teacher 모델과 Student 모델의 Softmax 출력 간의 KL Divergence의 가중 합으로 구성
  • 이 Loss Fucntion은 결국, Student 모델이 Teacher 모델의 지식을 효율적으로 학습하면서도 실제 레이블에 대한 정확도도 유지할 수 있도록 함
• Distillation Process:
  • Knowledge Distillation 과정에서는 Teacher 모델의 예측값과 Student 모델의 예측값 간의 차이를 줄이는 것이 목표
  • Soft Target을 통해 Student 모델이 Teacher 모델이 학습한 복잡한 패턴을 배우도록 함
  • Temperature 파라미터 $T$는 높은 값을 사용할수록 Teacher 모델의 예측 분포를 부드럽게 하여 Student 모델이 이를 더 쉽게 학습할 수 있도록 함
• Conclusions:
  • Student 모델이 더 적은 파라미터를 가지고 있음에도 불구하고 Teacher 모델의 성능에 근접한 결과를 얻을 수 있음
  • 이 방법은 특히 리소스가 제한된 환경에서 고성능의 작은 모델을 만들 때 유용

---

2. Romero et al., 2015

• Title: "FitNets: Hints for Thin Deep Nets"

• Summary: 중간 레이어의 표현을 활용하여 Student Model을 효과적으로 학습하는 방법을 제안, Hint layer 개념 도입

• Loss function

  • Teacher의 출력: $\mathbf{P_T} = softmax(\mathbf{a_T})$

  • Student의 출력: $\mathbf{P_S} = softmax(\mathbf{a_S})$

    $L_{KD}(\mathbf{W_S}) = \mathcal{H}(y_{true}, \mathbf{P_S}) + \lambda \mathcal{H}(\mathbf{P_T^T}, \mathbf{P_S^T})$
    

  • Hint-Based Training

    • FitNet의 중간 레이어와 Teacher 중간 레이어를 선택하여 Hint를 주입

    

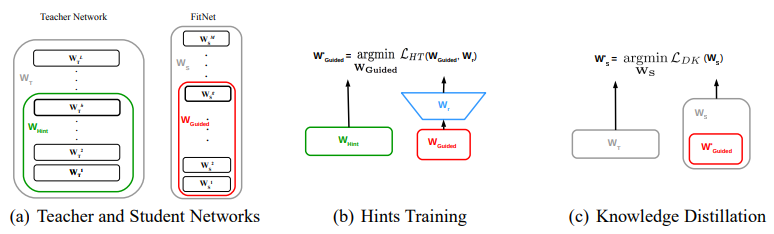
    • 다음 Loss function을 최소화하여 FitNet 파라미터를 학습

    • 해당 Loss는 Teacher의 Hint 레이어 출력과 Student의 중간 레이어 출력이 일치하도록 하는데 사용

    • 이를 통해 Student가 Teacher의 정보를 더 잘 학습할 수 있음

      $L_{HT}(\mathbf{W_{Guided}, W_r}) = \frac{1}{2} \|u_h(\mathbf{x}; \mathbf{W_{Hint}}) - r(v_g(\mathbf{x}; \mathbf{W_{Guided}}); \mathbf{W_r})\|^2$

---

3. Zagoruyko and Komodakis, 2017

• Title: "Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer"

• Summary: Attention 맵을 통해 Teacher Model의 중요 정보를 Student Model에 전달하는 방법을 제안함

  

• 인간은 attention을 통해 시각적 경험을 만들고 세부사항과 일관성을 가진 시각적 표상을 생성

• 이 때, CNN attention의 spatial map은 저수준, 중수준, 고수준의 representation을 capture 할 수 있음

  

• CNN 레이어의 activation tensor $A \in \mathbb{R}^{C \times H \times W}$

• 이 연구에서는 다음의 activation 기반 spatial attention map 사용

  • 절대값의 합: $F_{\text{sum}}(A) = \sum_{i=1}^C |A_i|$
  • $p$ 제곱된 절대값의 합 (where $p > 1$): $F^p_{\text{sum}}(A) = \sum_{i=1}^C |A_i|^p$
  • $p$ 제곱된 절대값의 최대값 (where $p > 1$): $F^p_{\text{max}}(A) = \max_{i=1,C} |A_i|^p$
  • $F^p_{\text{sum}}(A)$는 높은 activation 뉴런에 더 많은 가중치를 부여하여 가장 판별력이 높은 부분에 더 집중
  • $F^p_{\text{max}}(A)$는 해당 위치에 여러 뉴런이 높은 activation을 가진 경우 그 위치에 가중치를 부여

---

4. Jangho Kim, SeongUk Park, Nojun Kwak, 2018

• Title: "Paraphrasing Complex Network: Network Compression via Factor Transfer"

• Summary

  • 기존의 knowledge transfer 방법은 Teacher의 출력을 직접적으로 전달
  • 제안된 방법은 Teacher와 Student의 구조적 차이를 고려하여 Teacher의 출력을 재해석하고 전달
    

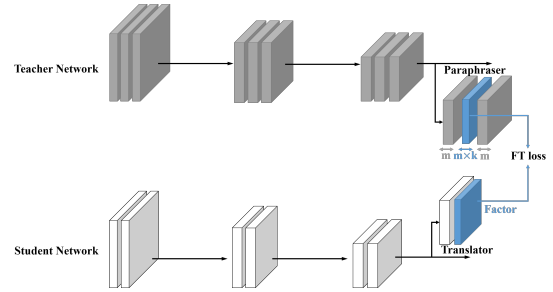
• Paraphraser의 중간 레이어 출력을 'Teacher factors'로 정의

• Translator 모듈을 사용하여 'Student factors'를 생성

• 이 과정은 두 단계로 구성

  1. Paraphraser가 reconstruction loss를 통해 학습

  2. Teacher factor가 Student 네트워크로 전이되어 Student이 이를 학습

     $L_{student} = L_{cls} + \beta L_{FT}$

     $L_{cls} = C(S(I_x), y)$

     $L_{FT} = \| \frac{F_T}{\|F_T\|_2} - \frac{F_S}{\|F_S\|_2} \|_p$

• Student는 classification loss와 factor transfer loss를 합한 loss function으로 학습

---

5. Park, W., Kim, D., Lu, Y., & Cho, M. (2019)

• Title: "Relational Knowledge Distillation"

• Summary

  • 이 논문은 Teacher Model과 Student Model 간의 관계 정보를 활용하여 Student Model이 Teacher Model의 지식을 학습하도록 하는 새로운 Knowledge Distillation 기법을 제안

  • 기존의 Knowledge Distillation 방법이 개별 데이터 예제의 출력을 모방하는 것과 달리, 이 방법은 데이터 간의 상호 관계를 학습하도록 유도

  • 논문에서는 두 가지 주요 Loss Fucntion인 Distance-wise Loss와 Angle-wise Loss를 제안하여 구조적 차이를 최소화하고, 모델 성능을 향상

  • Relational Knowledge Distillation (RKD)

    • Teacher Model과 Student Model 간의 예측값 간의 상호 관계를 학습하여 Knowledge Distillation의 효과를 극대화하는 방법

    

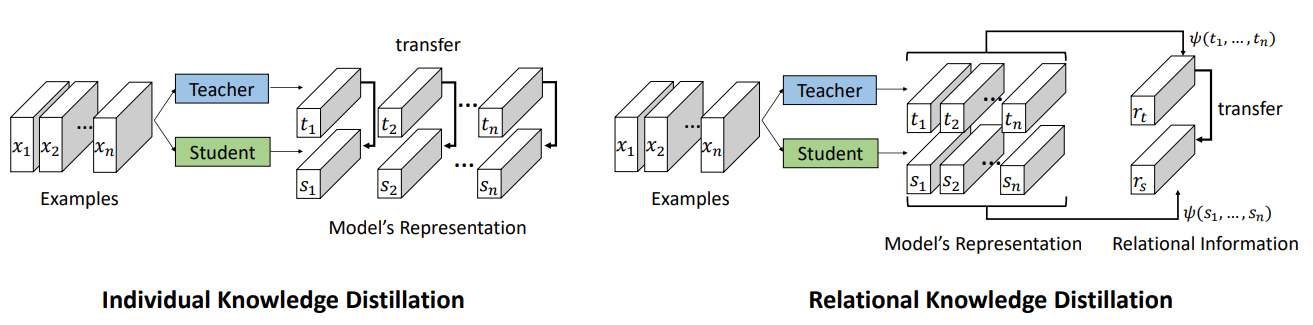
    • 기존의 방법들과 달리, RKD는 Teacher Model의 출력 간의 상호 관계, 예를 들어 샘플 간의 Distance나 Angle 정보를 Student Model이 학습하도록 유도

  • Loss Fucntion 정의

    1. Distance-wise Loss (Distance-wise Distillation Loss):
       이 Loss Fucntion은 Teacher Model과 Student Model 간의 데이터 샘플들 사이의 Distance 차이를 최소화하도록 유도

       • Distance Function 정의:
         두 샘플 $t_i$와 $t_j$ 사이의 Distance $\psi_D(t_i, t_j)$는 다음과 같이 정의

         $\psi_D(t_i, t_j) = \frac{1}{\mu} \|t_i - t_j\|^2$
         • $\|t_i - t_j\|^2$: 샘플 $t_i$와 $t_j$ 간의 Euclidean distance
         • $\mu$: Distance의 normalization factor로, 학습 샘플 간의 평균 Distance를 사용하여 Distance를 정규화

       • Distance-wise Loss 정의:
         Teacher Model과 Student Model 간의 Distance 차이를 최소화하기 위한 Loss Fucntion는 다음과 같음:

         $L_{\text{RKD-D}} = \sum_{(x_i, x_j) \in X^2} l_\delta(\psi_D(t_i, t_j), \psi_D(s_i, s_j))$
         • $l_\delta$: Huber Loss Fucntion(Huber Loss), Distance 차이가 작은 경우에는 Squared Error를 사용하고, 큰 경우에는 선형 오차를 사용하여 안정적인 학습을 제공
         • $s_i, s_j$: Student Model의 출력 샘플

    2. Angle-wise Loss (Angle-wise Distillation Loss):

       • 이 Loss Fucntion는 Teacher Model과 Student Model 간의 세 샘플이 형성하는 Angle 차이를 최소화하도록 유도

       • Angle Function 정의:

         • 세 샘플 $t_i, t_j, t_k$가 형성하는 Angle $\psi_A(t_i, t_j, t_k)$는 다음과 같이 정의:

           $\psi_A(t_i, t_j, t_k) = \cos\angle t_i t_j t_k = \langle e_{ij}, e_{kj} \rangle$

         • $\langle e_{ij}, e_{kj} \rangle$: 샘플 간의 단위 벡터(unit vector) 간의 내적(inner product)

         • $e_{ij} = \frac{t_i - t_j}{\|t_i - t_j\|}$, $e_{kj} = \frac{t_k - t_j}{\|t_k - t_j\|}$: 샘플 $t_i, t_j, t_k$ 간의 단위 벡터

       • Angle-wise Loss 정의:

         • Teacher Model과 Student Model 간의 Angle 차이를 최소화하기 위한 Loss Fucntion는 다음과 같음:
         $L_{\text{RKD-A}} = \sum_{(x_i, x_j, x_k) \in X^3} l_\delta(\psi_A(t_i, t_j, t_k), \psi_A(s_i, s_j, s_k))$
         • $l_\delta$: Huber Loss Fucntion

       • Final Loss Fucntion 정의

         • RKD의 최종 Loss Fucntion는 Distance-wise Loss과 Angle-wise Loss의 가중합으로 표현:
           $L_{\text{RKD}} = \alpha L_{\text{RKD-D}} + \beta L_{\text{RKD-A}}$
         • $\alpha$와 $\beta$: Distance loss와 Angle loss의 가중치로, 학습에서 각 loss term의 중요도를 조절

    Conclusions

    • Relational Knowledge Distillation은 기존의 Knowledge Distillation보다 Teacher Model과 Student Model 간의 관계를 더 잘 유지하도록 도와, 더 나은 성능을 달성할 수 있음
    • RKD는 Student Model이 Teacher Model의 출력 간의 관계를 학습하게 하여, 특히 Metric Learning과 같은 응용에서 뛰어난 성능을 보임
    • 실험 결과, RKD는 Student Model이 Teacher Model보다 더 나은 성능을 발휘하게 함을 보여주며, 다양한 태스크에서 높은 성능 향상을 달성